SOR和SSOR迭代

Posted 2023-02-01 陆嵩

SOR和SSOR迭代

基本思想

对于一般的大型稀疏方程组的求解，我们一般使用迭代方法求解，而古典的迭代方法中，松弛方法最优。对于Jacobi迭代，Gauss-Seidel迭代和（对称）超松弛方法迭代，我们可以简单地用矩阵分裂的思想来考虑这个问题，也可以从方程组的角度来理解这个问题。Jacobi迭代是将第i个方程中的第i个分量单独挪到一边，每个方程单独迭代的过程。Gauss-Seidel迭代是在Jacobi迭代过程中，对于迭代变量，求解方程中若某分量产生了新值用新值而不用旧值的过程，SOR迭代是在新值和旧值之间取个加权平均的过程。SSOR呢，是对于方程组，先用SOR方法从前往后（下三角用新值）算一遍，再用SOR方法从后往前（上三角用新值）算一遍的当成一次迭代的过程。从方程推导出的矩阵和分裂方法得到的结果是一样的。SSOR比起SOR更有可能收敛，并且对于权值来说不是太敏感。

一般来说SOR（包含了Gauss-Seidel）方法是优于Jacobi方法的，但是由于Jacabi良好的并行性质，使其仍存于世上。

对于对称正定矩阵，Jacobi迭代在$2D-A$正定时收敛，Gauss-Seidel方法收敛，SOR和SSOR收敛（$0<\omega <2$）。
对于严格对角占优和不可分弱严格对角占优矩阵（对角线不为零的是H矩阵），Jacobi迭代和Gauss-Seidel迭代收敛，SOR和SSOR在$0<\omega <2/[1+\rho (|J|)]$时收敛。

让人比较容易记住的是，矩阵分裂方法中，Jacobi迭代矩阵分裂出的M为对角矩阵，Gauss-Seidel迭代矩阵分裂出的M为下三角，SOR方法的迭代矩阵分裂出的M为下三角在对角元上再乘上$1/\omega$，与其对称的一个分裂出的M是上三角且对角元素乘以$1/\omega$。

需要指出的是，虽然SSOR比起SOR更稳定，收敛的可能性更大，但是有时候，其实在SOR收敛的情况下，最优SOR收敛可能比最优SSOR收敛得要快。所以，在实际使用中，我们还应该根据实际情况来选择迭代方式。对于非对称正定，对对角占优的矩阵，这些方法一般不收敛。

程序与结果

• C代码

  #include<stdlib.h>
  #include<stdio.h>
  #include<math.h>
  #include<string.h>
  #define N 5
  #define w 1
  #define epsilon 0.0000001
  void main()
  
      double normD(double x0[N], double x1[N]);
      void SORiteration1(double A[N][N], double b[N], double x0[N], double x1[N]);
      void SORiteration2(double A[N][N], double b[N], double x0[N], double  x1[N]);
      void triangularEquationsSolver(double T[N][N], double b[N], double x[N]);
      int i, j;
      static double A[N][N] =   5, 1, 1, 1, 1 ,  1, 5, 1, 1, 1 ,  1, 1, 5, 1, 1 ,  1, 1, 1, 5, 1 ,  1, 1, 1, 1, 5  ;
      double b[N] =  1.0, 1.0, 1.0, 1.0, 1.0 ;
      double x0[N] =  1.0, 1.0, 1.0, 1.0, 1.0 ;
      double x00[N] =  1.0, 1.0, 1.0, 1.0, 1.0 ;
      double xHf[N] =  0 ;
      double x1[N];
      do
      
          memcpy(x0, x1, N*sizeof(double));
          SORiteration1(A, b, x0, xHf);
          SORiteration2(A, b, xHf, x1);
  
  
       while (normD(x0, x1) > epsilon);
  
  
  
      printf("\\n要求解的示例方程组为：\\n A ||| b ||| x0\\n");
      for (i = 0; i < N; i++)
      
          for (j = 0; j < N; j++)
          
              printf("%f ", A[i][j]);
          
          printf("||| %f||| %f\\n", b[i], x00[i]);
      
  
      printf("\\n方程组解为：\\n");
      for (i = 0; i < N; i++)
      
          printf("%f\\n", x0[i]);
      
      getchar();
  
  
  double normD(double x0[N], double x1[N])
  
      int i;
      double s = 0;
      for (i = 0; i < N; i++)
      
          s = s + (x0[i] - x1[i])*(x0[i] - x1[i]);
      
      return sqrt(s);
  
  void SORiteration1(double A[N][N], double b[N], double x0[N], double x1[N])//传数组往往是传其地址
  
      void triangularEquationsSolver(double T[N][N], double b[N], double x[N]);
      //浪费一点内存没事，程序更具可读性。
      double Lwl[N][N] =  0 ;
      double Uwr[N][N] =  0 ;
      //double bb[N];
      int i, j;
      double wb[N];
      for (i = 1; i < N; i++)
      
          for (j = 0; j < i; j++)
          
              Lwl[i][j] = w*A[i][j];
              Uwr[j][i] = -w*A[j][i];
          
  
      
  
      for (i = 0; i < N; i++)
      
          Lwl[i][i] = A[i][i];
          Uwr[i][i] = (1 - w)*A[i][i];
          wb[i] = w*b[i];
      
  
  
  
      for (i = 0; i < N; i++)
      
          for (j = i; j < N; j++)
          
              wb[i] = wb[i] + Uwr[i][j] * x0[j];
          
  
      
      triangularEquationsSolver(Lwl, wb, x1);
  
      //printf("X1:\\n");
      //for (i = 0; i < N; i++)
      //
      //  printf("%f", x1[i]);
  
      //
      //getchar();
  
  
  
  
  
  void SORiteration2(double A[N][N], double b[N], double x0[N], double x1[N])
  
      void triangularEquationsSolver(double T[N][N], double b[N], double x[N]);
      //浪费一点内存没事，程序更具可读性。
      double Uwl[N][N] =  0 ;
      double Lwr[N][N] =  0 ;
  
      int i, j;
      double wb[N];
      for (i = 1; i < N; i++)
      
          for (j = 0; j < i; j++)
          
              Uwl[j][i] = w*A[j][i];
              Lwr[i][j] = -w*A[i][j];
  
          
  
      
      for (i = 0; i < N; i++)
      
          Uwl[i][i] = A[i][i];
          Lwr[i][i] = (1 - w)*A[i][i];
          wb[i] = w*b[i];
          for (j = 0; j < i; j++)
          
              wb[i] = wb[i] + Lwr[i][j] * x0[j];
          
  
      
      triangularEquationsSolver(Uwl, wb, x1);
  
  
  
  
  
  
  //求解上下三角方程的求解器
  void triangularEquationsSolver(double T[N][N], double b[N], double x[N])
  
      int i, j;
  
  
      //for (i = 0; i < N; i++)
      //
      //  for (j = 0; j < N; j++)
      //  
      //      printf("%f  ", T[i][j]);
      //  
      //  printf("\\n");
      //
      //getchar();
  
  
      if (T[0][N - 1] == 0)
      
          for (i = 0; i < N; i++)
          
              for (j = 0; j < i; j++)
              
                  b[i] = b[i] - T[i][j] * x[j];
              
              x[i] = b[i] / T[i][i];
  
          
      
      else
      
          for (i = N - 1; i >= 0; i--)
          
              for (j = i + 1; j < N; j++)
              
                  b[i] = b[i] - T[i][j] * x[j];
              
              x[i] = b[i] / T[i][i];
  
          
      
  
  

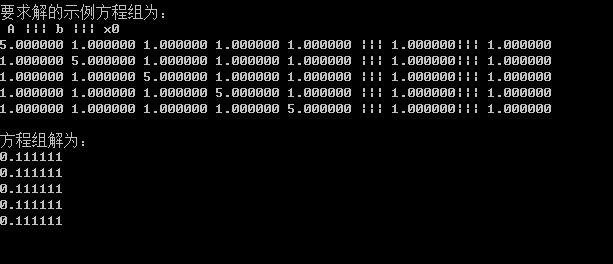
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bEBKt8ii-1574750026399)(pics/pic6.eps “fig:”)]width=“15cm”\\

• MATLAB代码

  clc
  clear
  w = 1;
  epsilon = 0.001;
  A = ones(5);
  for i = 1:5
      A(i,i) = 5;
  end
  b = ones(5,1);
  x0 = b;
  D = diag(diag(A));
  CL = -tril(A - D);
  CU = -triu( A - D);
  Lwl = D - w*CL;
  Uwr = w*CU + (1-w)*D;
  Uwl = D - w*CU;
  Lwr = w*CL + (1-w)*D;
  wb = w*b;
  while (1)
      xhf = Lwl\\(Uwr*x0+wb);
      x1 = Uwl \\ (Lwr*xhf + wb);
  %   x1 = Lwl\\(Uwr*x0+wb);
   %  x1 = (D-CL)^-1*CU*x0+(D-CL)^-1*b;
     if(norm(x0-x1,2)<epsilon),break;end
     x0 = x1;
  
  end
  x0
  A\\b
  wb
  

各种迭代简单的比较

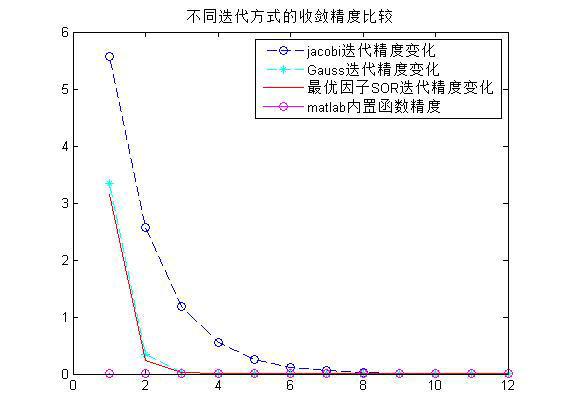
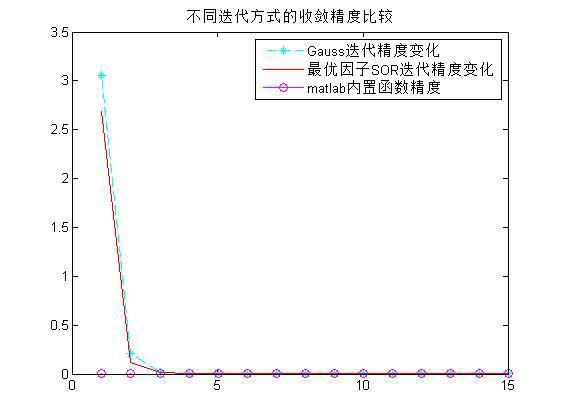
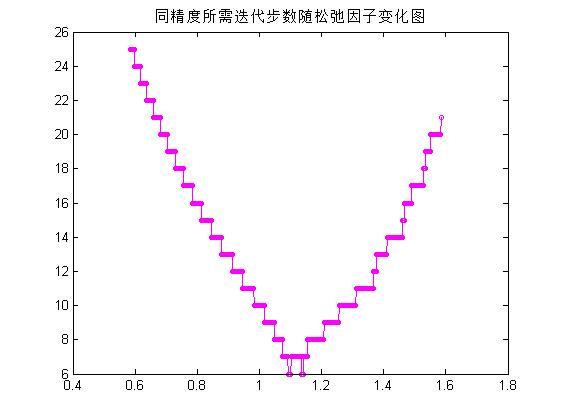
Jacobi迭代、Gauss-Seide迭代和最佳因子SOR迭代的比较，这里直接贴出结果：