C语言揭秘二战德军的顶级加解密技术——恩格玛机！

Posted 2023-01-12 C语言编程俱乐部

/ / 恩格玛机- 原理篇 \\ \\

非我德军不善战，奈何盟军有图灵

       二战战场上除了有纷飞的战火，还有科学家们在后方展开的斗智斗勇的密码战，而图灵破解了德国纳粹恩格玛密码机更是对德国纳粹的致命一击，直接加速了二战的胜利。（电影《模仿游戏》讲的就是这段历史，有兴趣的朋友可以了解一下。）

       恩格玛”（Enigma，谜）密码机是二战时期的纳粹德国及其盟国，特别是德国军方所使用的一种高级机械加密系统，以转子结构为主体。密码机一般装在一个盒子里。

       今天小编就和大家一起探讨一下恩格玛机如何用c语言实现。

       想要理解恩格玛机是如何运行的，首先要理解这种机器的加密原理。虽然恩格玛机看起来复杂，但它进行加密的基本原理并不复杂。这种机器所做的本质上是一种替换加密（Substitution Cipher）。

       不要被这个名字吓倒，我们首先来看一下替换加密是什么东西。

 

/ / 替换加密 \\ \\

       替换加密，又名取代加密，顾名思义，意为使用密文字母代替明文字母的位置，加密结束后，将会得到一段不经解密谁也看不懂的密文。听起来是不是很简单，让我们一起来看一个例子：

       首先给定简单替换加密的一个替换密码表：

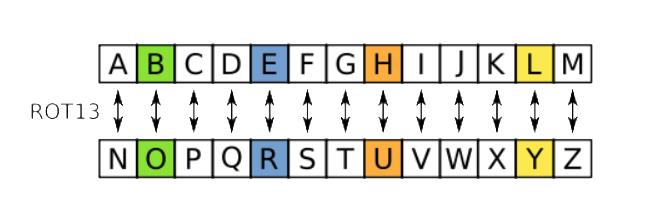
       如果我们想使用上面的替换密码表将 hello进行加密，只需要查询替换密码表，进行逐个替换即可。

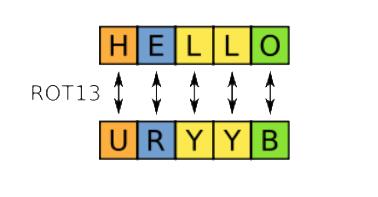
       因此HELLO加密后的密文就是URYYB。解密的时候同样根据替换密码表替换回原来的明文(是不是很简单)。

       如果直接使用暴力破解，26个字母的排列顺序有26!= 403291461126605635584000000 这么多种可能，这意味着如果全世界60亿人每人每秒可以测试一种可能的密码表，也需要21亿年才能试完所有的排列组合。事实上很长一段时间，这种简单的替换密码，被认为相当安全。

       直到。。。。

       有人用语言学和统计学的武器攻破了单表替换加密的大门。

       在使用字母文字的语言中，单个字母在普通文本中使用的概率是各不相同的，以英语为例，下面是摘自维基的英语文本中典型的字母分布情况：

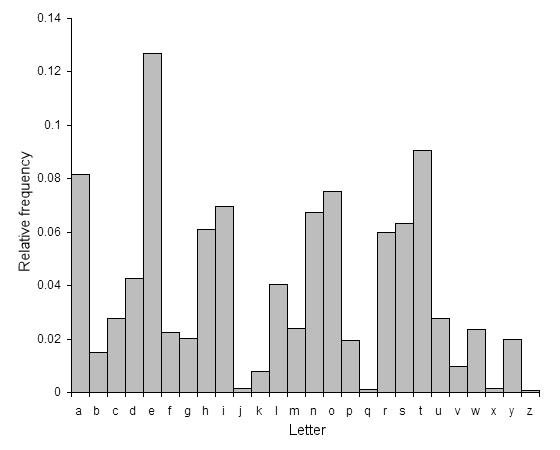
       仔细观察上图，上图中每个字母出现的频率都各不相同。

       我们刚刚使用的单边替换加密中，虽然每个字母都已经改头换面变成另一个字母，但是这并不能改变它在一段文本中出现的频率。因此我们完全可以统计密文中各个字母的出现频率，并试图猜测单表替换密码表（本质上就是建立一一映射关系），这样就能大大的减少要测试的排列数，进而完全破解密文。

       至此，我们上面介绍的单字母表替换加密被无情的破解了。于是不死心的密码学家们又发明了多字母替换密码。

       下面的内容逐渐进入烧脑状态，建议大家在头脑清醒时食用。

 

/ / 多字母替换加密 \\ \\

       单字母替换密码的一个致命缺陷就是明文中每一个字母都被唯一的替换为密文中的另一个字母（建立的一一映射关系不会发生改变）。

       破解者正是抓住了这个漏洞，结合语言学规律，对截获的密文进行字母频率分析，找到了这种一对一的替换关系，最终打败了密码学家们。

       在这个时候，顽强的密码学家们并不认输，谁规定只能使用一个密码表了，一个不行就用多个。让我们再举个例子：

       以二张密码表替换为例，首先给定二张密码表替换加密的替换密码表：

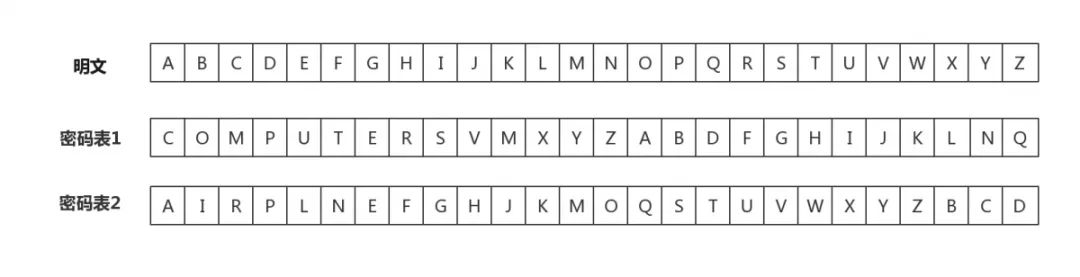
       与刚刚的单字母替换加密相比，我们又增加了一行密码表，有了这两行密码表，我们就可以在加密过程中对明文中的第1个字母使用密码表1进行加密，对第2个使用字母使用密码表2进行加密，第3个字母又重新使用密码表1加密，第4个字母使用密码表2，如此重复直到所有明文都被加密。

       大家可以试着用上图中多字母密码表加密下面这句话:

WHEN YOU ARE FREE

       注意到什么特别之处了吗？

       这句话中的第3个E会被替换为U，但是第10个字母同样是E，却会被替换为L，同一个明文字母由于位置的不同而被替换为不同的密文字母。也就是说，多字母替换密码不但可以替换掉明文中的字母，同时可以掩盖文中字母的出现频率。从而使破解使用的字母频率分析法立刻失效。

       密码学家们很是得意，他们继续问自己，既然可以使用两行密码表，为什么不能使用更多密码表呢，干脆让我们弄个25行的吧。

       上图就是著名的维热纳尔方阵，是为了方便加密者进行加密设计的替换密码表。

       有了多字母替换，这下密码学家们再也不用担心有人能破解了吧！

       让我们再来看一个例子。

       假设有一个勤劳的密码学家，为了得到一份绝对安全的密码，他不辞辛劳的打算使用7个密码表进行加密，假设这位密码学家打算使用上图的前7行进行加密。让我们用这种方法来加密下面这句话。

THE KING ,THE PEOPLE。

       加密后的结果如下图：

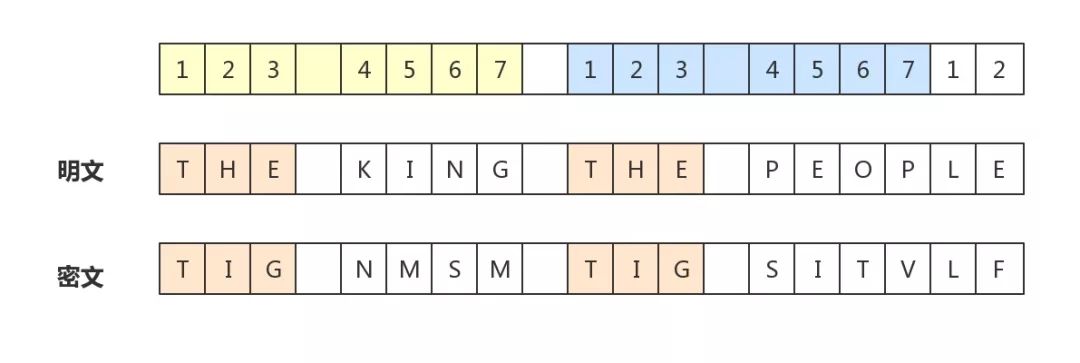
       大家仔细观察上图发现了什么呢？

       没错，同样的单词the在不同的位置居然被加密成了同一个字符串。原因就在于这个单词两个起始位置  mod 7 都是 1，这代表这两个不同位置的同一个单词，每个字母加密使用的密码表都是同一个，所以加密的结果当然也就相同了。

       破解者就是根据这个特性对重复出现的字母串进行分析，进而推算出密码学家一共使用了几个密码表进行加密。从而将多表替换降维成单表替换。

       在本例中，根据密文的重复序列很容易猜测使用了7个加密表，这就意味着，明文的第 1、8、15、22...个字母都是使用的同一张密码表进行替换，那么多个密码表替换问题又变成了单个密码表的替换问题。而上文我们已经发现了单字母表替换是无法抵抗频率攻击的。

       面对如此丧心病狂的破解者，无奈的密码学家们只能仰天长叹：”除非每加密一个字母就更换一次密码表并且永不重复，否则无论如何都逃不过被破解的命运。“

       “每加密一个字母就更换一次密码表并且永不重复“ 理论上是可以做到的，只是要加密一份有一万个字母的明文的话，就需要.... 额，一个长达一万行的密码本。这样就产生了密码本比密文本身还要长的尴尬局面。并且在军队中，每天有成千上万的信息在各地传送，如果为每条信息都创造一个随机密码表的话，如何保存，如何分配都是难以解局的问题。

       显然，这个任务已经超出了人类力所能及的范围。

 

/ / 恩格玛机 \\ \\

       不过人类做不到，不代表机器也做不到。

       这正是恩格玛机的过人之处，使用机械原理完成了大量重复有规律的劳动

       （叨叨了这么久终于讲到正题了）

       先上一张图看看恩格玛机的构造：

       上面这张图中可以看出，恩格玛机的四个主要部件：

       键盘：这个没什么好解释的，输入明文或者密文用的

       灯盘：在键盘上输入一个字母，灯盘上会有一个字母亮起来，代表键盘上输入的字母加密后的结果。

       转子：这个是恩格玛机的核心，是加密元件，后面进行解释。

       插线板：这是在转子进行加密后，为了提高安全性而增加的装置，不是本文的核心，这里不再赘述。

       恩格玛机的伟大之处就在于它在进行高度复杂的加密运算的同时，操作的简易性也几乎做到了极致。只需要简单的从键盘输入，就能从灯盘显示加密后的输出结果。真的是小学生都能用。

 

/ / 恩格玛机 - 转子 \\ \\ 

       讲完了恩格玛机我们再来看看恩格玛机的关键元件：转子

       图片左边是一个完整的转子，右边是一个转子拆开后的零件。

       转子的工作原理其实很简单，每个转子额左右两侧各有26个点位，分别代表A-Z 这26个字母。信号从一边进去，从另一边出来，但是在制造转子的过程中，位于转子左右两侧的26个字母的对应关系被打乱（单个转子的功能相当于一个单字母替换表）：

       下面是两张侧视图，可以更清楚的看到位于转子两侧的26个点：

       但是由于单个转子只能提供一个固定不变的密码表。因此并不安全。德国人当然也意识到了这一点，所以他们在恩格玛机上使用了三个串联在一起的转子，如下图：

       三个转子的替换就相当于一个三轮替换，但是我们上文已经分析发现，即使是多表替换也并不安全。单纯的将三个转子串联起来，他们还是只能提供一个固定不变的密码表。

       但是，当德国人在这三个转子上加入一个新的特性后，它就可以做到密码学家们梦寐以求的每加密一次就换一次密码表的效果。这个新特性就是：

       每输入一个字母以后，第一个转子就会自动转一格，当第一个转子转完一圈时，会带动第二个转子转动一格。同理，第二个转子转动一圈时会带动第三个转子转一格（类似于表盘上秒针、分针、时针的转动关系）。

       由于三个转子每个都有26种可能的位置，所以三个转子一共可以提供26^3=17576个不同的密码表。

       这个数字已经相当可观了，德国人不满足于此，又将三个转子设计为可以相互交换位置的形式。三个转子可以有3！= 6种不同的排列方式，所以密码表的数目又增加到 17576 X 6 = 105456，也就是大约十万个。

       但是德国仍然不满足，又增加了插线板和转子的数量，将密码数量进行一步扩大了1000亿倍。

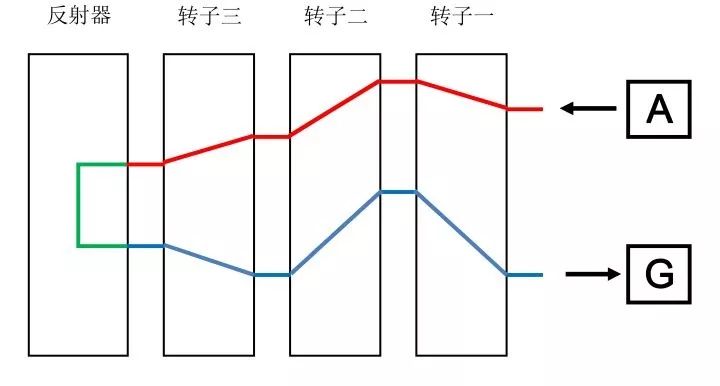
       下面是一张图，表示了信号从被输入转子开始，一直到加密完成从转子中输出的完整路径。

       大家可以看到字母A从键盘被输入，依次经过三个转子加密后到达反射器，然后在反射器这里又被替换成另一个字母，接下来又沿着转子返回加密，最终输出字母G。

/ / 恩格玛机 - 反射器 \\ \\ 

       有人会问为什么除了转子，还需要一个反射器？

       事实上，这个反射器的加入赋予恩格玛机两个非常重要的性质：

1、反射器使得恩格玛机的加密过程是自反的。也就是如果输入A得到G，那么在机器配置不变时，输入G一定会得到A。

2、一个字母的加密后的输出结果绝对不会是自身。

以下是对这两个性质如何得到的一些说明：

       1）转子配置不变，意味着字母从同一边到另一边走的永远是一条固定的路径，意味着上图中红色和蓝色路径是固定的，反射器不变，意味着绿色路径也是固定的。那么就意味着字母A沿着红色路线、绿色路线、蓝色路线，一定会得到字母G，同理，字母G沿着蓝色路线，绿色路线、红色路线也一定会得到字母A。

       2）性质二我们基于假设考虑一下：假如字母A想让加密结果是自己，那么它必须沿着红色路径进入，并且沿着红色路径返回才行，但是反射器的加入，强制输入输出不相等，导致上述条件永远得不到满足。

       第二个性质看起来是一个优点，毕竟把一个字母加密成自身不就等于没有加密吗？但是这个看似优点的性质日后反而成了恩格玛机的一个重要漏洞。在破解过程中被破解者狠狠利用了一把。

 

/ / 恩格玛机 - C语言实现 \\ \\

       恩格玛机的原理暂时先讲到这，现在让我们思考一下如何用c语言实现一个简易的恩格玛加密机。

       关键就在于使用循环模拟转子旋转的过程。

       一个简单的恩格玛机加解密实现代码如下，供大家参考：

#include<stdio.h>

#include<stdlib.h>

#include<string.h>

void Enigma(char input[20])

    int code;

    int n[4] = 24,2,5;  //定义3个转子

    int nsize=3;

    char output[20];

    for (int i = 0; i < strlen(input);i++)

    

        if(input[i]==' ')output[i] = ' ';continue;

        code = input[i]-'a';

        for (int j = 0; j < nsize;j++)

        

            code = (code + n[j]) % 26;

        

        if(code%2==0)  code++;else code--;  //反射器如果偶数+1，奇数-1，反射器只要能实现字母两两配对就可以了。

        for (int j = nsize-1; j >=0;j--)

        

            code = code - n[j];

            if(code<0)code=26+code;

        

        n[0]++;

        for (int j = 0; j < nsize-1; j++)

        

            if (n[j]>=26)

            

                n[j + 1]++;

                n[j] = 0;

            

        

        n[nsize-1] = n[nsize-1] % 26;

        output[i] = code+'a';

    

    printf("输出为: %s\\n",output);



int main()



char plain[20] = "hey hey  helloworld";

char cipher[20] = "ifz ifx  gdkmpvpske";

Enigma(plain);  //输入明文计算出密文

Enigma(cipher);  //输入密文计算出明文

//上述的两次调用体现了恩格码机的自反性

return 0;

---

对于热爱编程的人来说，有一群一起学习一起解答的小伙伴很重要！笔者有一个C语言/C++编程零基础入门学习交流俱乐部（点击进入），还有编程学习文件（源码，零基础教程，项目实战教学视频），欢迎初学者和正在进阶中的小伙伴们！