AOJ 2308 White Bird （极限情况）

Posted 2023-01-11 普通网友

White Bird

Time Limit : 5 sec, Memory Limit : 65536 KB

White Bird

Angry Birds is a mobile game of a big craze all over the world. You were convinced that it was a waste of time to play the game, so you decided to create an automatic solver.

You are describing a routine that optimizes the white bird's strategy to defeat a pig (enemy) by hitting an egg bomb. The white bird follows a parabolic trajectory from the initial position, and it can vertically drop egg bombs on the way.

In order to make it easy to solve, the following conditions hold for the stages.

• N obstacles are put on the stage.
• Each obstacle is a rectangle whose sides are parallel to the coordinate axes.
• The pig is put on the point (X,Y).
• You can launch the white bird in any direction at an initial velocity V from the origin.
• If the white bird collides with an obstacle, it becomes unable to drop egg bombs.
• If the egg bomb collides with an obstacle, the egg bomb is vanished.

The acceleration of gravity is 9.8m⁄s2. Gravity exerts a force on the objects in the decreasing direction ofy-coordinate.

Input

A dataset follows the format shown below:

N V X Y
L1 B1 R1 T1
…
LN BN RN TN

All inputs are integer.

• N: the number of obstacles
• V: the initial speed of the white bird
• X, Y: the position of the pig

(0≤N≤50, 0≤V≤50, 0≤X,Y≤300, X≠0)

for 1≤i≤N,

• Li: the x-coordinate of the left side of the i-th obstacle
• Bi: the y-coordinate of the bottom side of the i-th obstacle
• Ri: the x-coordinate of the right side of the i-th obstacle
• Ti: the y-coordinate of the top side of the i-th obstacle

(0≤Li,Bi,Ri,Ti≤300)

It is guaranteed that the answer remains unaffected by a change of Li, Bi, Ri and Ti in 10−6.

Output

Yes/No

You should answer whether the white bird can drop an egg bomb toward the pig.

Sample Input 1

0 7 3 1

Output for the Sample Input 1

Yes

Sample Input 2

1 7 3 1
1 1 2 2

Output for the Sample Input 2

No

Sample Input 3

1 7 2 2
0 1 1 2

Output for the Sample Input 3

No

---

Source: ACM-ICPC Japan Alumni Group Summer Camp 2011 , Day 3, Tokyo, Japan, 2011-09-19 

http://acm-icpc.aitea.net/

题意：

平面上有N个障碍物，i号障碍物是左下角为（Li，Bi），右上角为（Ri，Ti）的与坐标轴平行的长方形。从原点以初速度V向任意角度发射一只白鸟。设重力加速度沿y轴负方向，大小为9.8，射出的鸟将呈抛物线飞出，直到撞到障碍物为止。鸟可以在中途产一枚卵，所产的卵将沿y轴负方向竖直落下，直到撞到障碍物为止。请问是否可以让卵击中坐标位于（X,Y）的猪。

分析：

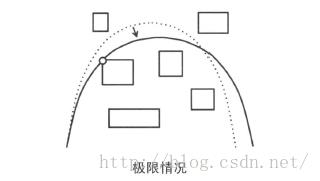
最后的限制条件常常会在几何问题中附带出现，根据这一点就无需考虑只有通过像穿过针孔一样的唯一线路才能让卵击中猪的情况了。首先，让我们来考虑一下如何判断以某个角度射出的鸟是否可以产卵击中猪。只要射出的鸟在撞到障碍物之前能够从猪的正上方飞过，并且此时与猪之间没有障碍物的话，在正上方产卵就可以击中猪了。判断白鸟是否撞到障碍物，就是判断抛物线和长方形是否相交（如果将长方形分解为线段，只判断抛物线是否同各条线段相交，就可能无法很好地处理抛物线恰好经过长方形的顶点的情况，需要注意），稍加计算即可完成。

接下来，我们思考一下应该如何枚举所有关键射出角度。假设以某个角度射出时不会撞到障碍物，我们逐渐降低这个高度，直到某处变成

1）       恰好经过(X,Y)

2）       恰好经过某个障碍物的左上角或右上角

就不能再降低了。虽然作为解的角度可能有无穷多个，但因为无论哪个都可以不断降低直至变为1或2的情况，所以只要检查这些角度就足够了。

#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxn = 55;
const double g = 9.8;   //重力加速度
const double EPS = 1e-10;
int N;
double V, X, Y;
double L[maxn], B[maxn], R[maxn], T[maxn];

//计算以vy的速度竖直向上射出t秒后的位置
double calc(double vy, double t)

    return vy * t - g * t * t / 2;


//a相对lb和ub的位置
int cmp(double lb, double ub, double a)

    return a < lb + EPS ? -1 : a > ub - EPS ? 1 : 0;


//判断当射出路径经过点(qx, qy)时，卵是否能击中猪
bool check(double qx, double qy)

    //设初速度在x方向和y方向的分量分别为vx和vy，设通过(qx, qy)的时间为t
    //设解联立方程式vx^2 + vy ^2 = V^2, vx * t = 1x, vy * t - 1/2 g t^2 = qy
    double a = g * g / 4, b = g * qy - V * V, c = qx * qx + qy * qy;
    double D = b * b - 4 * a * c;
    if (D < 0 && D > -EPS)
        D = 0;
    if (D < 0)
        return false;
    for (int d = -1; d <= 1; d += 2)       //验证联立方程式上的两个解的循环
        double t2 = (-b + d * sqrt(D)) / (2 * a);
        if (t2 <= 0)
            continue;
        double t = sqrt(t2);
        double vx = qx / t, vy = (qy + g * t * t / 2) / t;

        //判断是否通过猪的正上方
        double yt = calc(vy, X / vx);
        if (yt < Y - EPS)
            continue;

        bool ok = true;
        for (int i = 0; i < N; i++)
            if (L[i] >= X)
                continue;
            //判断在猪正上方的鸟和猪之间是否有障碍物
            if (R[i] == X && Y <= T[i] && B[i] <= yt)
                ok = false;
            //判断在飞到猪的正上方之前是否会撞到障碍物
            int yL = cmp(B[i], T[i], calc(vy, L[i] / vx));   //左侧的相对位置
            int yR = cmp(B[i], T[i], calc(vy, R[i] / vx));   //右侧的相对位置
            int xH = cmp(L[i], R[i], vx * (vy / g));      //最高点的相对位置
            int yH = cmp(B[i], T[i], calc(vy, vy / g));
            if (xH == 0 && yH >= 0 && yL < 0)
                ok = false;
            if (yL * yR <= 0)
                ok = false;
        
        if (ok)
            return true;
    
    return false;


void solve()

    //截掉猪以右的障碍物
    for (int i = 0; i < N; i++)
        R[i] = min(R[i], X);
    
    bool ok = check(X, Y);      //直接撞上猪的情况
    for (int i = 0; i < N; i++)
        ok |= check(L[i], T[i]);     //经过左上角的情况
        ok |= check(R[i], T[i]);     //经过右上角的情况
    
    puts(ok ? "Yes" : "No");


int main()

    while (scanf("%d%lf%lf%lf", &N, &V, &X, &Y) != EOF)
        for (int i = 0; i < N; i++)
            scanf("%lf%lf%lf%lf", &L[i], &B[i], &R[i], &T[i]);
        
        solve();
    
    return 0;