3. 监督学习之回归及归纳偏好

Posted 2023-01-06 starrow

1.1.2 回归

同样，用一个简单的例子来说明回归。这次我变成一个天气爱好者，想知道每天不同时间的气温。预测函数的输入是时间，输出是该时间的气温。回归也需要训练数据，这里的数据是我记录的一天当中若干时刻的气温。如图1.6所示，横轴代表一天的时间，不妨设原点左边为白天，右边为晚上；纵轴代表气温。横轴上标出的几个点代表记录气温的时间，其上方的点表示所记录的气温值。

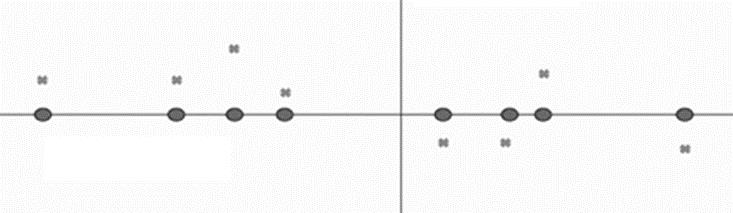
 图1.6 一天当中几个时刻记录的气温

原始的方法是将所有训练数据的点连起来，两点之间可以用直线，也可以用曲线，如图1.7所示。然而正如卖车的例子，这样一条复杂的曲线很可能不是我们想要的函数，因为根据常识判断，位于夜晚部分的那个气温突起不太正常，该数据实例很可能是噪声。

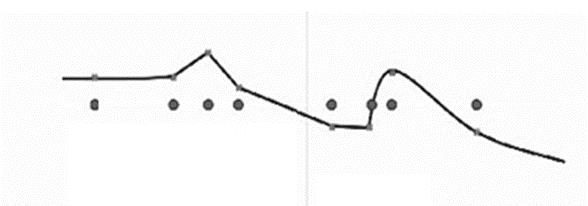
图1.7 用一条复杂的曲线拟合的气温数据

回到问题的原点，我们希望画出气温随时间变化的曲线，它不必在每个记录的时刻与实际气温相等，但必须使误差尽可能小。那么应该如何度量误差呢？最简单的想法是直接计算误差之和，但这样会导致正负误差相互抵消。便于计算的解决方法是先对误差求平方后再加和。此外，回归曲线自然是越简单越好。于是，我们的目标是在各个记录时刻预测气温的误差平方之和最小的直线，如图1.8所示。这即是著名的采用最小二乘法的线性回归。

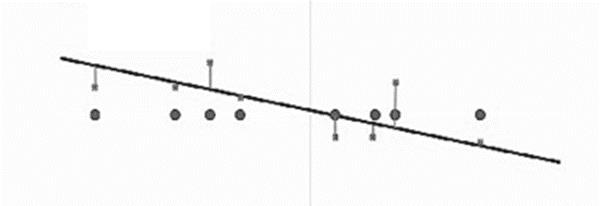
图1.8 气温对时间进行线性回归得出的直线

除了预测，回归还可以用于数据压缩、趋势分析和因子分析等许多场景：遇到大量数据难以存储和传输时，可以通过回归将数据约简为一个函数，不仅实现了数据量的高度压缩，还相当于分析出了其中的变化趋势，回归函数中各输入变量的系数则体现了输入变量对输出值的贡献。分类也能藉回归进行。比如，在卖汽车的例子中分别用数字+1和–1来代表是否买车的类别，则可以让其对年龄和收入回归。进行预测时，若回归函数值为正数，则将顾客分入+1的类别；若函数值为负数，则将顾客分入–1的类别。

1.1.3 归纳偏好

聪明的读者或许有疑问，上述分析只是找到某个尽可能符合训练数据的函数，凭什么确定可以用它进行预测？换言之，对于训练数据以外的实例，怎么知道其输入值和输出值符合训练数据所符合的函数关系？理论上，可以定义无数个函数，契合训练数据而在其他输入值处具有任意输出值。因此，如果对一般输入和输出所符合函数的性质、类型或形式不做任何假定，是不可能进行预测的。而对预测函数的这些假定就称为归纳偏好（Inductive bias）或学习偏好（Learning bias）。

给数字序列找规律的智力题能够形象地说明归纳偏好。例如，写出此序列的下一个数字：2、5、10、17。大家很快就会想出答案26，原因为每个数字都是其序号的平方加1。但实际上，设该序列为某个函数的自变量分别为1、2、3和4时的函数值，可以列出无数满足条件的函数。而且，无论将下一个数字写为多少，都能找到它与前4个数字共同符合的函数或规律。比如，取下一个数字为0，用拉格朗日插值法可以得出符合该序列的一个多项式函数为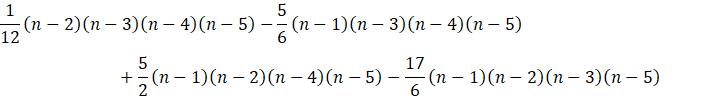 。我们之所以更认可答案26，是因为它对应的函数n^2 + 1更简单。

 从上述例子可以引出哲学上著名的奥卡姆剃刀（Occam's razor）原则，用归纳偏好的语言来说，就是预测函数在符合训练数据的前提下越简单越好。比如，在1.1.1节中，用于划分类别的曲线越简单越好。在1.1.2节中，预测函数采用最简单的线性函数。在后面的章节中，我们会看到各式各样的归纳偏好。3.2节介绍的变量选择和3.3节介绍的正则化，共同之处是减少预测函数的输入变量。7.1.3节的最小描述长度认为描述一个学习模型的代码越短，该模型就越好。这些归纳偏好都体现了奥卡姆剃刀的原则。由于归纳偏好是对预测函数性质、类型或形式的假定，所以从不同的偏好能建立起各异的学习模型。例如，从线性函数的偏好建立起第3章的线性回归和第4章的线性分类模型，从预测函数值局部不变的偏好建立起2.4节的K近邻模型，从输入变量关于类别独立的偏好建立起4.3.4节的单纯贝叶斯模型。

从上述例子和论述，可以总结监督学习的一般过程。用X表示某任务的输入变量，Y表示输出变量。模型的归纳偏好规定X和Y之间存在特定形式的函数关系Y = f(X)，利用训练数据估计出其中的参数，得到可用于预测的函数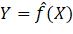  ，如图1.9所示。

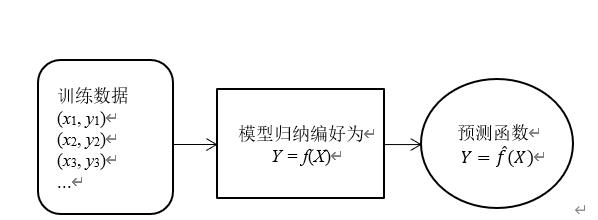
 图1.9 监督学习的过程

在得到预测函数后，需要以某种方法评估它应用于训练数据以外实例时的表现。最常用的方法是交叉验证（Cross-validation）：将已有的数据实例分为训练数据集和验证数据集，验证数据集用于计算函数在训练数据集以外的预测误差。然后，通过比较一系列函数的预测误差，选出表现最好者。