网格去噪的几种算法（利用Laplacian矩阵）

Posted 2023-01-02 拉风小宇

最近在做网格去噪的东西，看了几篇文章，值得推荐的是“Vertex-Based Diffusion for 3-D Mesh Denoising”这篇文章，基本讲清楚了几种去噪方式的理论。

在Toolbox graph工具箱中提供了三种去除噪声的算法，都是利用离散的Laplacian算子和Laplacian矩阵，下面分别介绍

Laplacian光滑

是最常用的方法，他利用如下规则同时并且重复地调整每个顶点的位置到其相邻点的几何中心

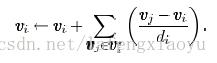
尽管Laplacian光滑很简单快速，但是会造成曲面的收缩，并且会有过度光滑的问题。我们先来看一下这种算法的实现过程

function [W,L]  = compute_mesh_laplacian_combinatorial( ~,face )
%CPMPUTE_MESH_LAPLACIAN_COMBINATORIAL Summary of this function goes here
%   Detailed explanation goes here


W = triangulation2adjacency(face);
W = diag(sum(W,2).^(-1)) * W;
n = size(W,1);
L = speye(n) - diag(sum(W,2).^(-1)) * W;

end

W是邻接矩阵，之后进行单位化，L是其对应的Laplacian矩阵

其中，triangulation2adjacency.m是

function A = triangulation2adjacency(face,vertex)

% triangulation2adjacency - compute the adjacency matrix
%   of a given triangulation.
%
%   A = triangulation2adjacency(face);
% or for getting a weighted graph
%   A = triangulation2adjacency(face,vertex);
%
%   Copyright (c) 2005 Gabriel Peyr


[tmp,face] = check_face_vertex([],face);
f = double(face)';

A = sparse([f(:,1); f(:,1); f(:,2); f(:,2); f(:,3); f(:,3)], ...
           [f(:,2); f(:,3); f(:,1); f(:,3); f(:,1); f(:,2)], ...
           1.0);
% avoid double links
A = double(A>0);

return; 


nvert = max(max(face));
nface = size(face,1);
A = spalloc(nvert,nvert,3*nface);

for i=1:nface
    for k=1:3
        kk = mod(k,3)+1;
        if nargin<2
            A(face(i,k),face(i,kk)) = 1;
        else
            v = vertex(:,face(i,k))-vertex(:,face(i,kk));
            A(face(i,k),face(i,kk)) = sqrt( sum(v.^2) );    % euclidean distance
        end
    end
end 
% make sure that all edges are symmetric
A = max(A,A');

测试代码如下

[vertex,face]=obj__read('mannequin.obj');
normals = compute_normal(vertex,face);
rho = randn(1,size(vertex,2))*4;
vertex1 = vertex + repmat(rho,3,1).*normals;
[W,L]=compute_mesh_laplacian_combinatorial( vertex,face );
vertex2 = vertex1;
for i=1:3
subplot(1,3,i);
trep=triangulation(face',vertex2');
trimesh(trep);axis square;axis off;
vertex2 = (W*(W*vertex2'))';
end

前面几行代码是加噪声，后面为算法的实现

效果如下图

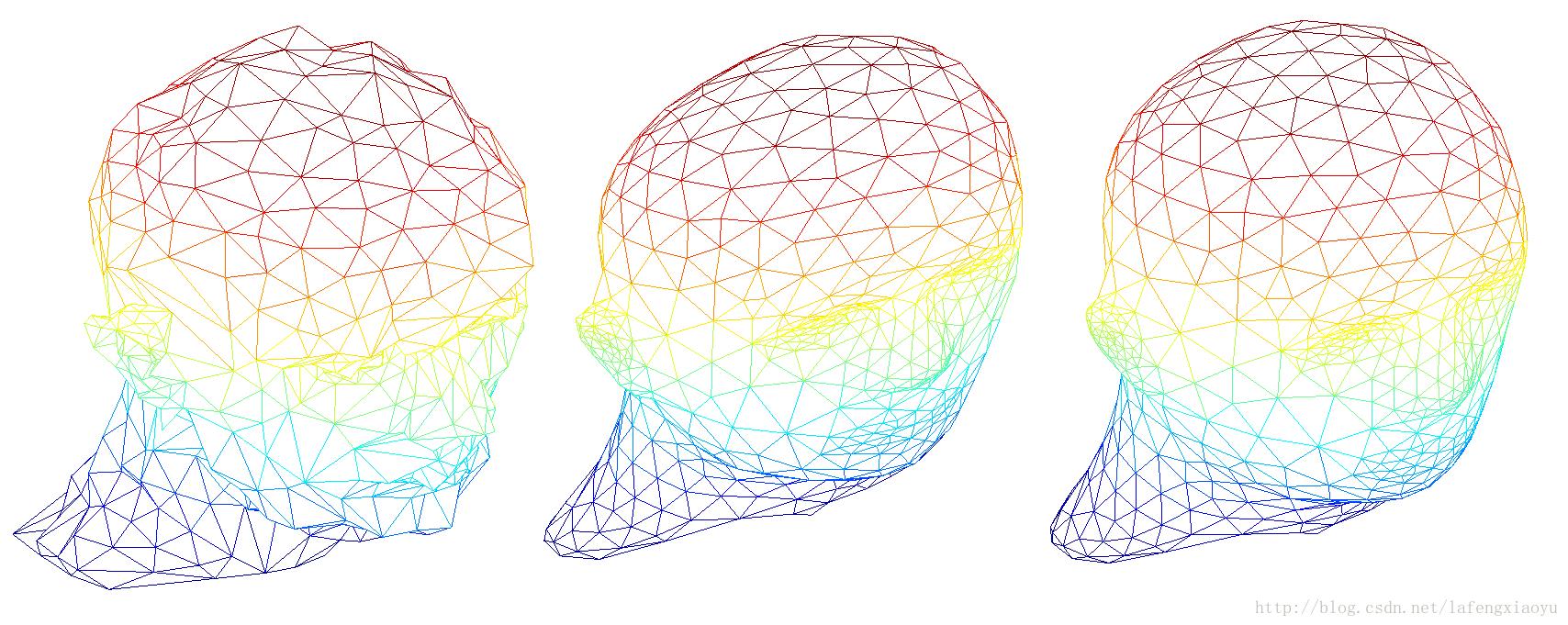所以之后介绍的相当于是加权的Laplacian光滑

按照距离加权的Laplacian光滑

改变了W和L的算法，根据两点间的欧氏距离（边长）进行加权，更新之前得到的W矩阵

function  [W,L]  = compute_mesh_laplacian_distance( vertex,face )
%COMPUTE_MESH_LAPLACIAN_DISTANCE Summary of this function goes here
%   Detailed explanation goes here
W = my_euclidean_distance(triangulation2adjacency(face),vertex);
W(W>0) = 1./W(W>0);
W = (W+W')/2; 
W = diag(sum(W,2).^(-1)) * W;
n = size(W,1);
L = speye(n) - diag(sum(W,2).^(-1)) * W;

end


function W = my_euclidean_distance(A,vertex)

if size(vertex,1)<size(vertex,2)
    vertex = vertex';
end

[i,j,s] = find(sparse(A));
d = sum( (vertex(i,:) - vertex(j,:)).^2, 2);
W = sparse(i,j,d);
end

同样用上面的人脸进行测试

[vertex,face]=obj__read('mannequin.obj');
normals = compute_normal(vertex,face);
rho = randn(1,size(vertex,2))*4;
vertex1 = vertex + repmat(rho,3,1).*normals;
[W,L]=compute_mesh_laplacian_distance( vertex,face );
vertex2 = vertex1;
for i=1:3
subplot(1,3,i);
trep=triangulation(face',vertex2');
trimesh(trep);axis square;axis off;
vertex2 = (W*(W*vertex2'))';
end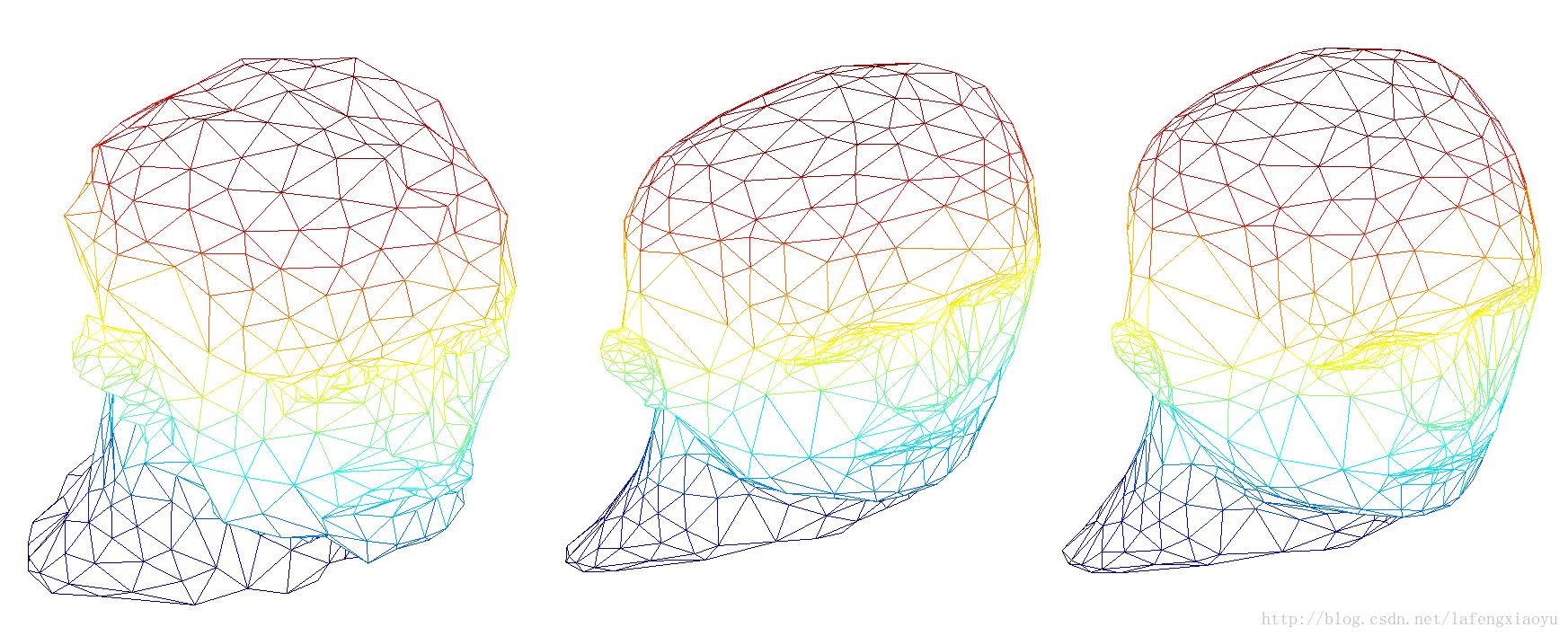

只是改变了一句话而已，下面看效果

按照曲率法向加权

该方法是在Implicit fairing of irregular meshes using diffusion and curvature flow文章里提出的，边权重由下面的式子给出

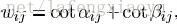
其中两个角由下图中的角vivj-1vj和vivj+1vj表示

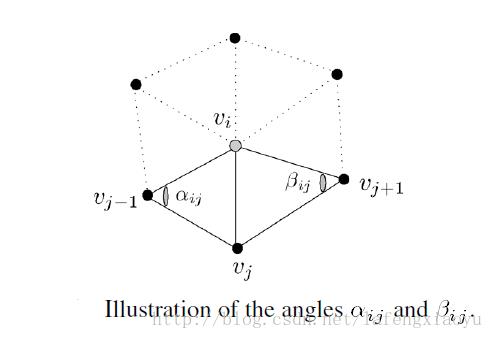
之后，更新规则改为

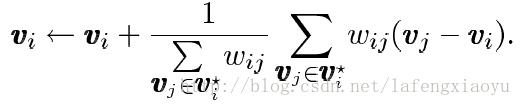
改进的边权重用来补偿三角网格的不规则从而避免所有的边被同等对待，实现的代码如下compute_mesh_laplacian_combinatorial.m

function [W,L]  = compute_mesh_laplacian_combinatorial( vertex,face )
%CPMPUTE_MESH_LAPLACIAN_COMBINATORIAL Summary of this function goes here
%   Detailed explanation goes here

n = max(max(face));
% conformal laplacian
W = sparse(n,n);
ring = compute_vertex_face_ring(face);
for i = 1:n
    for b = ringi
        % b is a face adjacent to a
        bf = face(:,b);
        % compute complementary vertices
        if bf(1)==i
            v = bf(2:3);
        elseif bf(2)==i
            v = bf([1 3]);
        elseif bf(3)==i
            v = bf(1:2);
        else
            error('Problem in face ring.');
        end
        j = v(1); k = v(2);
        vi = vertex(:,i);
        vj = vertex(:,j);
        vk = vertex(:,k);
        % angles
        alpha = myangle(vk-vi,vk-vj);
        beta = myangle(vj-vi,vj-vk);
        % add weight
        W(i,j) = W(i,j) + cot( alpha );
        W(i,k) = W(i,k) + cot( beta );
    end
end
W = diag(sum(W,2).^(-1)) * W;
n = size(W,1);
L = speye(n) - diag(sum(W,2).^(-1)) * W;

end


function beta = myangle(u,v)

du = sqrt( sum(u.^2) );
dv = sqrt( sum(v.^2) );
du = max(du,eps); dv = max(dv,eps);
beta = acos( sum(u.*v) / (du*dv) );
end

function ring = compute_vertex_face_ring(face)

% compute_vertex_face_ring - compute the faces adjacent to each vertex
%
%   ring = compute_vertex_face_ring(face);
%
%   Copyright (c) 2007 Gabriel Peyr?

[~,face] = check_face_vertex([],face);

nfaces = size(face,2);
nverts = max(face(:));

ringnverts = [];

for i=1:nfaces
    for k=1:3
        ringface(k,i)(end+1) = i;
    end
end
end

这次拿大象举例

[vertex,face]=obj__read('elephant.obj');
normals = compute_normal(vertex,face);
rho = randn(1,size(vertex,2))*.02;
vertex1 = vertex + repmat(rho,3,1).*normals;
[W,L]=compute_mesh_laplacian_combinatorial( vertex,face );
vertex2 = vertex1;
for i=1:3
subplot(1,3,i);
trep=triangulation(face',vertex2');
trimesh(trep);axis square;axis off;
vertex2 = (W*(W*vertex2'))';
end

很明显效果非常好，但是对人脸貌似有奇异值出现。。明天我查一查