matlab实现封闭四边形网格的Catmull-Clark细分（CC细分）

Posted 2023-01-02 拉风小宇

之前的一篇文章：网格细分算法（Catmull-Clark subdivision & Loop subdivision）附源码阅读量还很大，但是其实代码有一点小问题，在这里我暂且先把封闭网格的代码改好，至于任意四边形网格，会在后面的博客中体现。

输入的V是nV*3个点的数据，F是nF*4个面的数据，iter表示迭代次数，缺省的时候为1，输出的是新的点面，完整代码如下

function [VV, FF] = CCsub(V, F, iter)  
    % Catmull_Clark subdivision  
    if ~exist('iter','var')  
        iter = 1;  
    end  
    VV = V;  
    FF = F;  
      
    for i = 1:iter
        
        nv = size(VV,1);  
        nf = size(FF,1);  
                 
        original = 1:nv;  
        boundary = [];  
        interior = original(~ismember(original, boundary)); 
          
        no = length(original);   
        ni = length(interior);  
  
        %% Sv  
        Etmp = sort([FF(:,1) FF(:,2);FF(:,2) FF(:,3);FF(:,3) FF(:,4);FF(:,4) FF(:,1)],2);  
        [E, ~, idx] = unique(Etmp, 'rows');  
          
        Aeven = sparse([E(:,1) E(:,2)], [E(:,2) E(:,1)], 1, no, no);  
        Aodd = sparse([FF(:,1) FF(:,2)], [FF(:,3) FF(:,4)], 1, no, no);  
        Aodd = Aodd + Aodd';  
          
        val_even = sum(Aeven,2);  
        beta = 3./(2*val_even);  
          
        val_odd = sum(Aodd,2);  
        gamma = 1./(4*val_odd);  
          
        alpha = 1 - beta - gamma;  
          
        Sv = sparse(no,no);  
        Sv(interior,:) = ...  
            sparse(1:ni, interior, alpha(interior), ni, no) + ...  
            bsxfun(@times, Aeven(interior,:), beta(interior)./val_even(interior)) + ...  
            bsxfun(@times, Aodd(interior,:), gamma(interior)./val_odd(interior));  
          
        %% Sf  
        Sf = 1/4 .* sparse(repmat((1:nf)',1 ,4), FF, 1);  
        i0 = no + (1:nf)';  
          
        %% Se  
        flaps = sparse([idx;idx], ...  
                       [FF(:,3) FF(:,4);FF(:,4) FF(:,1);FF(:,1) FF(:,2);FF(:,2) FF(:,3)], ...  
                       1);  
        onboundary = (sum(flaps,2) == 2);  
        flaps(onboundary,:) = 0;  
          
        ne = size(E,1);  
        Se = sparse( ...  
                [1:ne 1:ne]', ...  
                [E(:,1); E(:,2)], ...  
                [onboundary;onboundary].*1/2 + ~[onboundary;onboundary].*3/8, ...  
                ne, ...  
                no) + ...  
                flaps*1/16;  
          
        %% new faces & new vertices  
        i1 = no +   nf + (1:nf)';  
        i2 = no + 2*nf + (1:nf)';  
        i3 = no + 3*nf + (1:nf)';  
        i4 = no + 4*nf + (1:nf)';  
          
        FFtmp = [i0 i4 FF(:,1) i1; ...  
                 i0 i1 FF(:,2) i2; ...  
                 i0 i2 FF(:,3) i3; ...  
                 i0 i3 FF(:,4) i4];  
  
        reidx = [(1:no)'; no+(1:nf)'; no+nf+idx];  
        FF = reidx(FFtmp);  
          
        S = [Sv; Sf; Se];  
        VV = S*VV;  
    end  
 end  

测试以一个正六面体和环为例

[V,F]=obj__read('torus.obj');
V=V';F=F';
iter=2;
[VV, FF] = CCsub(V, F, iter);
obj_write('torus1.obj',VV',FF');

效果如下

圆环

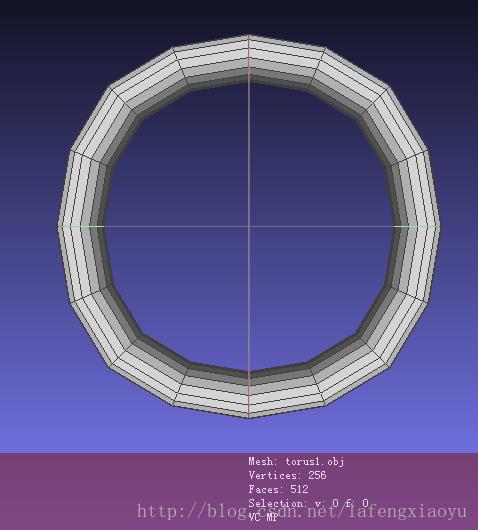初始圆环	细分两次

正方体

原始正方体	细分两次