2023数据结构考研复习-树
Posted ZSYL
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2023数据结构考研复习-树相关的知识,希望对你有一定的参考价值。
2023数据结构考研复习-树(五)
树的定义
#include <iostream>
using namespace std;
struct Node
int data;
Node *l, *r;
struct LinkNode
Node *data; // 存指针
LinkNode *next;
struct Queue
LinkNode *front, *rear;
先序遍历
// 函数调用栈,保存当前调用的函数信息
void preOrder(Node root)
if (root)
cout << root.data << endl;
preOrder(root.l);
preOrder(root.r);
双while循环先序遍历:
public List<Integer> preorderTraversal(Node root)
List<Integer> list= new ArrayList<>();
Stack<Node> stack = new Stack<>();
while(!stack.isEmpty() || root != null)
while(root != null)
list.add(root.val);
stack.push(root);
root=root.left;
root = stack.pop();
root = root.right;
return list;
压栈操作:
public List<Integer> preorderTraversal(Node root)
if (root == null) return new ArrayLIst<>();
List<Integer> list= new ArrayList<>();
Stack<Node> stack = new Stack<>();
stack.push(root);
while(!stack.isEmpty())
Node cur = stack.pop();
list.add(cur.val);
if(cur.right != null) stack.push(cur.right);
if(cur.left != null) stack.push(cur.left);
return list;
后序遍历
双while循环后序遍历,左右中,中右左reverse就行:
public List<Integer> preorderTraversal(Node root)
List<Integer> list= new ArrayList<>();
Stack<Node> stack = new Stack<>();
while(!stack.isEmpty() || root != null)
while(root != null)
list.add(root.val);
stack.push(root);
root=root.right;
root = stack.pop();
root = root.left;
return list;
双while循环后序遍历:
public List<Integer> preorderTraversal(Node root)
List<Integer> list= new ArrayList<>();
Stack<Node> stack = new Stack<>();
while(!stack.isEmpty() || root != null)
while(root != null)
stack.push(root);
root=root.left;
root = stack.pop();
list.add(root.val);
root = root.right;
return list;
树的深度
// 树的深度
int treeDepth (Node root)
if (root == NULL)
return 0;
int l = treeDepth(root.l);
int r = treeDepth(root.r);
return l > r ? l+1 : r+1;
层次遍历
// 层次遍历
void LevelOrder(Node root)
Queue Q;
initQueue(Q);
Node p;
add(root);
while (!isEmpty(Q))
poll(Q, p);
visit(p);
if (p.l)
add(p.l);
if (p.r)
add(p.r);
线索二叉树
#include <iostream>
using namespace std;
struct Node
int data;
Node *l, *r;
int ltag, rtag; // tag=0指向左右孩子结点,tag=1指向线索(l:前驱,r:后继)
// 辅助全局变量,用于查找结点p的前驱
Node *p; // p指向目标结点
Node *pre = NULL; // 指向当前访问的前驱
Node *final = NULL; // 用于记录最终结果
// 中序线索化
void createInThread(Node *root)
pre = NULL;
if (root != NULL) // 非空二叉树才能线索化
InThread(root);
if (pre.r == NULL)
pre.rtag = 1; // 处理遍历的最后一个结点
// 函数调用栈,保存当前调用的函数信息
void InThread(Node root)
if (root)
InThread(root.l);
visit(root);
InThread(root.r);
// 先序线索化
void InThread(Node root)
if (root)
visit(root);
if (root.ltag == 0) // lchild不是前驱线索
InThread(root.l);
InThread(root.r);
// 土方法找到中序前驱
void visit(Node *q)
if (q == p) // 当前访问结点刚好是结点p
final = pre; // 找到p的前驱
else
pre = q; // pre指向当前结点
// 线索化查找前驱
void visit(Node *q)
if (q.l == NULL)
q.l = pre;
q.ltag = 1;
if (pre != NULL && pre.r == NULL)
pre.r = q;
pre.rtag = 1;
pre = q;
// 找到以root为根的子树中,第一个被中序遍历的结点
Node *FirstNode (Node *root)
while (root.ltag == 0)
root = root.l;
return root;
// 中序线索二叉树中找到结点p的后继结点
Node *NextNode (Node *root)
// 右子树中最左下的结点
if (root.rtag == 0)
return FirstNode(root.r);
else
return root.r;
// 对中序线索二叉树进行中序遍历(利用线索实现的非递归算法)
void Inorder(Node *root)
for (Node *p=Firstnode(root); p!= NULL; p=Nextnode(p))
visit(p);
// 找到以root为根的子树中,最后一个被中序遍历的结点
Node *LastNode (Node *root)
while (root.rtag == 0)
root = root.r;
return root;
// 中序线索二叉树中找到结点p的前驱结点
Node *PreNode (Node *root)
// 右子树中最右下的结点
if (root.ltag == 0)
return LastNode(root.r);
else
return root.l;
// 对中序线索二叉树进行逆向的中序遍历(利用线索实现的非递归算法)
void Rev Inorder(Node *root)
for (Node *p=Lastnode(root); p!= NULL; p=Prenode(p))
visit(p);
双亲表示法
#include <iostream>
using namespace std;
#define Maxsize=100
// 双亲表示法
struct Node
int data;
int parent; // 双亲位置域
;
struct Tree
Node nodes[Maxsize]; // 双亲表示
int n; // 结点数
;
// 孩子表示法
struct Node
int data;
Node *next; // 双亲位置域
;
struct Box
int data;
Node *firstChild; // 双亲位置域
;
struct Tree
Box nodes[Maxsize]; // 双亲表示
int n, r; // 结点数和根的位置
;
// 孩子兄弟表示法
struct Node
int data;
Node *firstchild, *nextsibling; // 二叉链表,第一个孩子和有兄弟指针
;
综合应用
1. 后序遍历二叉树的非递归算法
算法思想:后序非递归遍历二叉树是先访问左子树,再访问右子树,最后访问根结点。结合图5.7来分析:①沿着根的左孩子,依次入栈,直到左孩子为空。此时栈内元素依次为ABD。读栈顶元素:若其右孩子不空且未被访问过,将右子树转执行①;否则,栈顶元素出栈并访问。栈顶D的右孩子为空,出栈并访问,它是后序序列的第一个结点;栈顶B的右孩子不空且未被访问过,E入栈,栈顶E的左右孩子均为空,出栈并访问;栈顶B的右孩子不空但已被访问,B出栈并访问;栈顶A的右孩子不空且未被访问过,C入栈,栈顶C的左右孩子均为空,出栈并访问;栈顶A的右孩子不空但已被访问,A出栈并访问。由此得到后序序列DEBCA。
在上述思想的第②步中,必须分清返回时是从左子树返回的还是从右子树返回的,因此设定一个辅助指针r,指向最近访问过的结点。也可在结点中增加一个标志域,记录是否已被访问。
void postOrder(BiTree T)
InitStack(S);
p = T;
r = NULL;
while (p || !IsEmpty(S))
if (p) // 走到最左边
push(S, p)
p = p->lchild;
else
GetTop(S, p);
if (p->rchild && p->rchild != r) // 左子树存在且未被访问过
p = p->rchild; // 转向右边
else
pop(S, p);
visit(p->data);
r = p;
p = NULL;
注意:每次出栈访问完一个结点就相当于遍历完以该结点为根的子树,需将p置NULL。
2. 二叉树的自下而上、从右到左的层次遍历算法
试给出二叉树的自下而上、从右到左的层次遍历算法。
一般的二叉树层次遍历是自上而下、从左到右,这里的遍历顺序恰好相反。算法思想:利用原有的层次遍历算法,出队的同时将各结点指针入栈,在所有结点入栈后再从栈顶开始依次访问即为所求的算法。具体实现如下:
1)把根结点入队列。
2)把一个元素出队列,遍历这个元素。
3)依次把这个元素的左孩子、右孩子入队列。
4)若队列不空,则跳到2),否则结束。
void InvertLevel(BiTree bt)
Stack s, Queue q;
if (bt)
InitStack(s);
InitQueue(q);
Enqueue(Q, bt);
while (Isempty(q) == false)
Dequeue(Q, p);
push(s, p);
if (p->lchild)
Enqueue(p->lchild);
if (p->rchild)
Enqueue(p->rchild);
while (Isempty(s) == false)
Pop(s, p);
visit(p->data);
3. 非递归求二叉树高度
假设二叉树采用二叉链表存储结构,设计一个非递归算法求二叉树的高度。
采用层次遍历的算法,设置变量level记录当前结点所在的层数,设置变量last指向当前层的最右结点,每次层次遍历出队时与last指针比较,若两者相等,则层数加1,并让last指向下一层的最右结点,直到遍历完成。level的值即为二叉树的高度。
int Btdepth(BiTree T)
if (!T)
return 0;
int front = -1, rear = -1;
int last = 0, level = 0;
BiTree Q[MAXSIZE];
Q[++rear] = T;
Bitree p;
while (front < rear)
p = Q[++front];
if (p->lchild)
Q[++rear] = p->lchild;
if (p->rchild)
Q[++rear] = p->rchild;
if (front == last)
level++;
last = rear;
4. 先序&中序序列建树
设一棵二叉树中各结点的值互不相同,其先序遍历序列和中序遍历序列分别存于两个一维数组A[1…n]和B[ 1…n]中,试编写算法建立该二叉树的二叉链表。
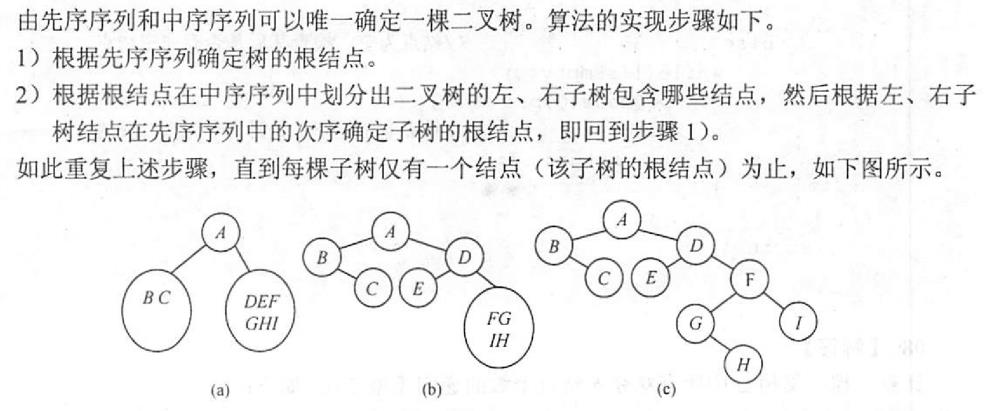
BiTree PreInCreate(int a[], int b[], int a1, int a2, int b1, int b2)
// 初始调用:a1 = a2 = 1, b1 = b2 = n; a1,b1为先序的第一个和最后一个的下标
root = (BiTNode*)malloc(sizeof(BiTNode));
root->data = a[a1]; // 先序序列第一个即为根结点
for (i = l2; b[i] != root->data; i++); // 根结点在中序序列中的位置
llen = i - a2; // 中序中位置-起始位置即为左子树长度
rlen = b2 - i; // 中序末尾位置-根结点所在位置即为右子树长度
if (llen) // 递归建立左子树,先序起始位置+1,末尾为起始位置+llen,中序起始位置不变,末尾为起始位置+llen-1(在先序中划分左子树)
root->lchild = PreInCreate(a, b, a1+1, a1+llen, b2, b2+llen-1);
else
root->lchild = NULL;
if (rlen) // 递归建立右子树,先序起始位置从尾巴位置前移右子树长度+1,末尾不变,中序起始位置从尾巴位置前移rlen+1,末尾不变(在先序中划分左子树)
root->rchild = PreInCreate(a, b, b1-rlen+1, h1, h2-rlen+1, h2);
else
root->rchild = NULL;
return root; // 返回根结点指针
5. 判定完全二叉树
二叉树按二叉链表形式存储,写一个判别给定二叉树是否是完全二叉树的算法。
根据完全二叉树的定义,具有n个结点的完全二叉树与满二叉树中编号从1~~n的结点一一对应。
算法思想:采用层次遍历算法,将所有结点加入队列(包括空结点)。遇到空结点时,查看其后是否有非空结点。若有,则二叉树不是完全二叉树。
bool isComplete(BiTree T)
InitQueue(Q);
if (!T)
return 1;
EnQueue(Q, T);
while(!IsEmpty(Q))
DeQueue以上是关于2023数据结构考研复习-树的主要内容,如果未能解决你的问题,请参考以下文章