论文阅读：Practical Deep Raw Image Denoising on Mobile Devices

Posted 2022-12-23 Matrix_11

论文阅读： Practical Deep Raw Image Denoising on Mobile Devices

旷视 2020 ECCV

基于深度学习的降噪方法在近几年得到了大量的研究，这些方法的效果也霸榜了很多公开的数据集。不过这些方法用到的网络模型都很大，无法在手机端侧运行。这篇文章的作者设计了一种能够在手机端运行的轻量级地的降噪模型，而且在主流的旗舰机上还取得了不错的效果。这篇文章的方法有两个关键点：1) 通过对特定 sensor 的噪声模型进行标定，可以在特定噪声模型上去模拟数据从而指导小网络训练，这样的方式甚至比用大网络在基于一般的噪声模型模拟的数据训练的效果要好；2) 虽然对于特定 sensor 来说，不同 ISO 下的噪声形态会有较大差异，不过这篇文章的作者利用一个 K-simga 变换让这些不同的噪声形态变换之后变得比较统一，从而让小网络可以更好地进行处理。文章提到在手机端侧高通 855 平台的运行时间是 70ms 左右。

Introduction

随着智能手机的普及，越来越多的用户用智能手机来满足日常拍照摄影的需求。不过比起单反来说，智能手机由于镜头以及 sensor 上的制约，在夜景中更容易出现噪声。

图像降噪技术经过了十几二十年的发展，但是在手机上实现高质量的降噪依然是一个很大的挑战。最近随着深度学习的兴起，很多基于深度学习的方法取得了比传统方法更好的降噪效果，但是深度学习模型相对来说也很大，所以对在智能手机上用深度模型做降噪依然面临很多困难。

这篇文章的作者提出了一种简单而有效的方法来实现 RAW 域的降噪，文章的作者基于一个关键的观测，即对于某一款特定的 sensor 来说，噪声特性是连续的，并且可以很准确地测量出来。通过对 sensor 的噪声建模，就可以构建有噪声与干净图像的数据对，然后训练一个轻量级的网络，这个基于模拟数据训练的模型，在真实拍摄的数据上，依然可以有效地进行降噪，而且，基于噪声参数模型，文章作者设计了一种单一的线性变换，称为 K-sigma 变换，这个变换可以将不同 ISO 下的噪声形态变换到一个与 ISO 无关的噪声形态。这样可以很方便地对不同 ISO 下的噪声进行降噪。

Method

Noise Model

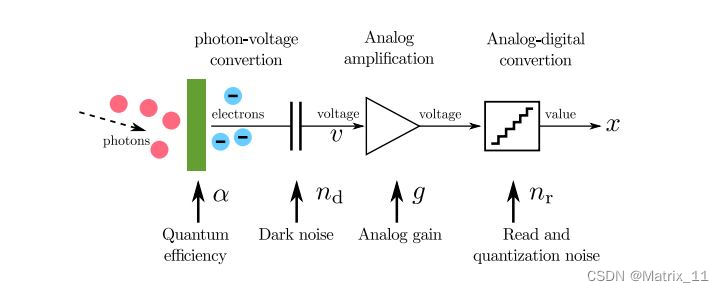
在 ISP 中，一个 Camera sensor 将入射的光线通过多个转换步骤，最后得到数字信号，每个转换步骤都可能引入特定的噪声，首先考虑一个理想的光电转换系统，每个像素的电路将光子通过一个线性放大系统转换为电信号：

$$x^{\ast }=g\alpha u^{\ast }$$

$u^{\ast }$ 表示照射到每个 pixel 上的平均期望光子数，$\alpha$ 表示光电转换效率，$g$ 表示模拟增益。

在一个实际的系统中，如果考虑每一步引入的噪声，则有：

$$x=g(\alpha u+n_d)+n_r$$

其中，$u$ 表示实际的光子数，$n_d\sim \mathcal{N}(0,{\sigma }_d^2)$ 和 $n_r\sim \mathcal{N}(0,{\sigma }_r^2)$ 是满足高斯分布的噪声，其中 $u$ 是服从期望为 $u^{\ast }$ 的泊松分布:

$$u\sim \mathcal{P}(u^{\ast })$$

结合上面的式子，可以得到：

$$x\sim (g\alpha )\mathcal{P}(\frac{x^{\ast }}{g\alpha })+\mathcal{N}(0,g^2{\sigma }_d^2+{\sigma }_r^2)$$

上面的式子，就是我们常见的泊松-高斯分布，如果令 $ k = g \\alpha$，同时 $\\sigma^2 = g^2 \\sigma_d^2 + \\sigma_r^2 $，那么上面的泊松-高斯分布可以写成：

$$x\sim k\mathcal{P}(\frac{x^{\ast }}{k})+\mathcal{N}(0,{\sigma }^2)$$

其中 $k$ 和 $\sigma$ 都是和 ISO 相关的参数。

Parameter Estimation

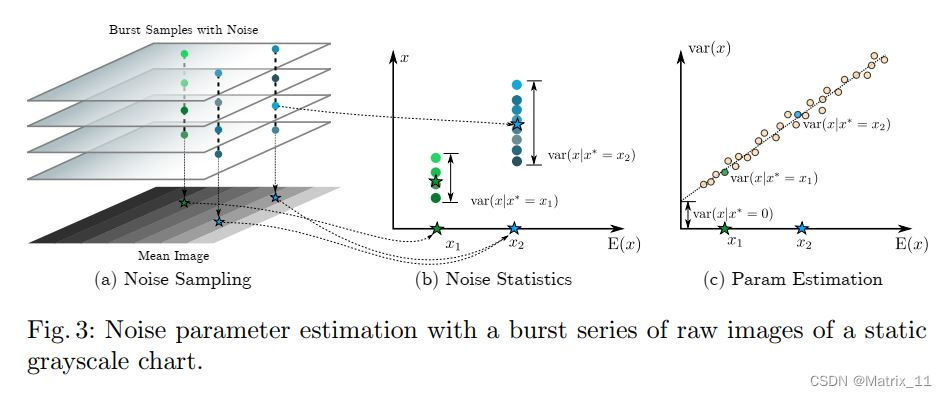
有了上面的噪声模型，理论上来说，我们可以通过采样获取不同的噪声样本，从而构建数据对，因为 $k$ 和 $\sigma$ 都是和 ISO 相关的参数，一般来说，就需要对不同的 ISO 下进行 $k$ 和 $\sigma$ 的标定，不过，文章作者通过分析上面式子的期望均值与方差，发现他们满足如下的关系式：

$$E(x)=x^{\ast }$$

$$Var(x)=k{x}^{\ast }+{\sigma }^2$$

文章的作者拍了一组静态的灰卡，然后将这些灰卡取平均值来获得期望均值， 同时将有同样平均值的像素值聚到一起，计算其方差，然后利用一个线性函数拟合得到 $k,{\sigma }^2$。

The k-Sigma Transform

在实际应用场景中，摄像头会根据实际的场景，自动调整 ISO，所以对于一个降噪模型来说，需要考虑到不同的 ISO。一种直观的方法，就是将不同 ISO 的 $k,{\sigma }^2$ 都计算出来，然后构造不同 ISO 下的训练数据对，从而训练这个降噪模型，这样对网络的 Capacity 就有一定的要求。文章作者提出了一种 k-sigma 变换的方法，将不同 ISO 下的噪声形态进行了统一。

这个 k-sigma 变换的定义如下：

$$f(x)=\frac{x}{k}+\frac{{\sigma }^2}{k^2}$$

由 $x$ 的噪声分布，可以得到 $f(x)$ 的分布如下所示：

$$f(x)\sim \mathcal{P}(\frac{x^{\ast }}{k})+\mathcal{N}(\frac{{\sigma }^2}{k^2},\frac{{\sigma }^2}{k^2})$$

泊松-高斯分布可以通过下面的近似变换成高斯分布：

$$\begin{array}{rl}& \mathcal{P}(\frac{x^{\ast }}{k})+\mathcal{N}(\frac{{\sigma }^2}{k^2},\frac{{\sigma }^2}{k^2})\\ & \approx \mathcal{N}(\frac{x^{\ast }}{k}\\ & \\ & \end{array}$$

论文阅读｜深读SDNE:Structural Deep Network Embedding

Deep Knowledge Tracing with Transformers论文阅读

CV论文阅读Deep Linear Discriminative Analysis, ICLR, 2016

Deep Residual Learning for Image Recognition(ResNet)-论文阅读笔记

论文阅读｜深读DANE:Deep Attributed Network Embedding

论文阅读｜深读DRNE:Deep Recursive Network Embedding with Regular Equivalence