基础算法系列--[基本数据结构&KMP]

Posted 2022-12-21 Huterox

文章目录

• 前言
• 链表
• • 单链表
  • 双链表
• 栈和队列
• • 栈
  • 队列
  • 单调
• KMP

前言

今天要搞的是基本的一些数据结构，当然咱们这个不是那么“正经”。当然今天也没啥代码，因为太简单了（其实我也想水一下~）

链表

单链表

单链表这个东西，应该都知道，就是一个这个玩意：

好处：

1. 可以一直存嘛
2. 方便在后面插入元素嘛
   但是缺点呢，在这里的话我们原来是用Node然后用next指针去指向下一个元素来做。但是这个node是一个自定义的一个结构，这样就导致每次需要创建比较麻烦。

那么我们这边就是说用数组去模拟这个链表，同样的这个数组可以是动态的比如Java里面的ArrayList或者直接Python里面的，当然用python的选择要更多。
总之为了高效嘛，我们用数组来实现呗，只要我具备了单链表的特质，你管我怎么实现是吧。

那么这个怎么干呢：

其实就这样干就完了。

一开始value的第一个元素就是头结点，这里我们也是需要一个head，也就是头结点，有可能删除头结点（一开始的）所以还是需要这个head，因为删除没有办法真的删除，或者说如果要删除，问题就很慢了，换一句话说，适合解题，我们的目的也是解题。

双链表

至于这个双链表的话，那就是再加入一个数组存储pre就好了

栈和队列

OK，接下来的话，我们再来看到这个栈还队列，同样的我们要使用这个数组来做一个模拟。这个的话其实更加简单，这里的话我们就直接看到伪代码好吧：

栈

这里我们用C++的伪代码来写一下，这个更直观一点：

#include<iostream>
using namespace std;
const int N =2022;

int stk[N],tt;
//insert
stk[++t]=x;
//pop
tt--;
if(tt>0)
	not empty
else
	empty
//stack top
stk[tt];

差不多就这样一个栈就好了

队列

队列的话也是一样类似的

#include<iostream>
using namespace std;
const int N=2022;
int q[N],hh,tt=-1;

//insert
q[++tt]=x
// out 
hh++;

if(hh<=tt)
	not empty
else
	empty
//get head
q[hh];
//get end
q[tt]

单调

然后说完了这个的话，有啥用呢，首先这个的话会比较快，当然缺点也就是刚刚那个嘛，是一个伪删除。不过这个也无所谓，能够快速执行就完了。然后的好处呢就是快，毕竟比较原始的玩意嘛。

然后的话这里面用自己写的这种栈，队列之类的话，用单调队列，单调栈的时候的话，可以比较好的考虑到这个。

像一些滑动窗口的题目可以考虑用单调队列去做，去年的时候，好像做过一道题目来自，好像是在letcode里面。这里的话我就不去找例题了。就单纯说一下思想吧。
首先单调栈，单调队列其实都是类似的。核心其实就是利用单调的一些性质，或者利用马尔科夫性。
那么这个玩意的话大概其实就是这样的。
假设有这样的一种题目，给你一个序列，然后呢，叫你找到每一个数字中左边最近的最小的数，或者最大的数字的时候。那么这个时候的话我们可以考虑直接使用单调栈，假设找最小的。那么你只需要准备一个栈。每次遍历的时候呢，去栈里面判断，把栈里面的比他小的元素输出就好了。也就是说，你只要保证你的栈，是单调递增的就可以。为什么这样就可以呢，我们可以简单画一个数轴：

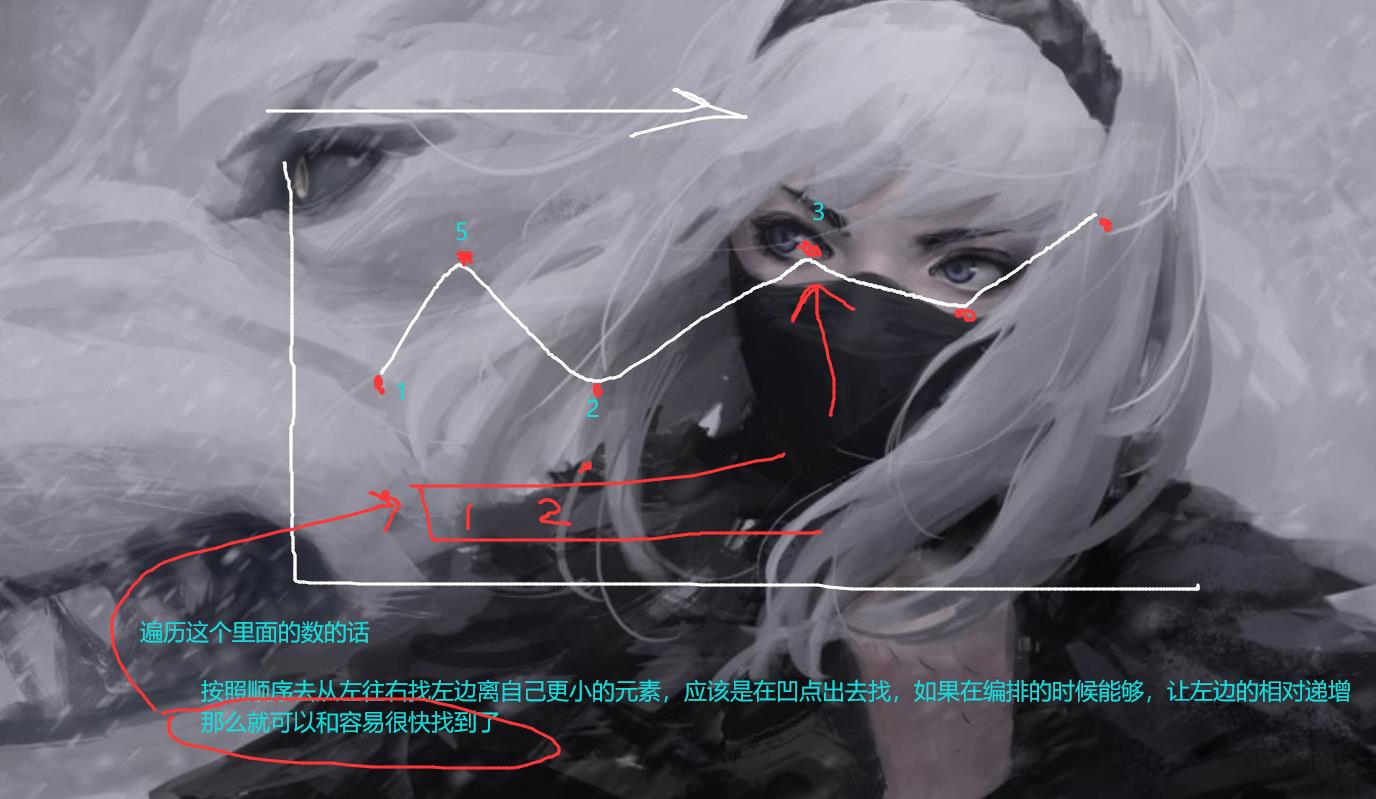
这个的话大概有点抽象，反正就是这个意思。

还有就是使用单调队列的一种题目，这个的话原理大概也是类似的。找不到原题了，我大概描述一下是这样的：
给一个数列，在区间大小为K的子数列里面找到找到最小值，从左到右依次序滑动。

那么这个题目的思路其实是类似的，保证单调就好了，这里保证队头最小就好了，然后输出队头的元素。但是比较特殊的就是，也是因为我们的这个删除问题，我们的队列里面得存储下标就好了。用这个的原因的话，就是为了避免重复的一个比较，重复的排序。画一个数轴表示大概是这样的：

没找到原题，这个代码暂时就先这样吧。

KMP

这个算法的话，算了，还是说一下吧。

这个的话，其实挺简单的，搞清楚它的一个核心思想其实就很简单了，我们先不管什么前缀，后缀，什么乱七八糟的概念。从简，我就就直接看到最朴素的做法。然后从朴素的做法里面去找到它的一个思想，就是怎么偷懒。

这样的话，我们不就偷到一点懒了嘛。
这个不就是大部分男人滴最爱“KMP”嘛（像博主一样及其关注了博主的帅小伙除外）

那么搞清楚了，我们要想办法用这种方式来偷懒，那么我们就可以很好滴搞清楚这个KMP算法了。

OK，那么我们要做的呢就是说如何去想办法知道，最长的玩意，那么我们这边有一个数组叫做next数组，在kmp算法里面。

那么这个数组是什么玩意呢，他其实是这样的：

next[i]=j

这个是什么意思呢，就是说这样

Str[1~j]=Str[i-j+1,i]

假设从开始，第i个字符前的j个字符连起来和字符一开始到第j个字符是一样的。

这个就是所谓next数组，那么这个时候的话，有两个点第一个点就是怎么用这个next，然后就是如何求取next。
首先是怎么用。用的话非常简单，其实就是说，对比被，假设P是我们的被匹配的字符串，S是我们用来匹配的字符串（就是图里面的蓝色的线）。当在P当中的第i个字符和我们匹配字符串的第j个字符不相等的时候，那么前面的j-1字符是和前面的i-1都是相等的对吧。假设现在next[j-1]=3，那么意味着前面三个字符和头部的三个字符都是相等的对吧，再假设下标是从0开始的，那么这个时候，我们P字符串的第i个元素，是不是只需要从S字符串的下标为3的那个字符再开始比较就好了。因为第i-1,i-2,i-3和我们的S的0,1，2（下标）的字符是相等的。

所以用的话你会发现是这样用的：
（这个是以前的java代码）

      for (int i = 0, j = 0; i < n; i++) 
            while (j > 0 && haystack.charAt(i) != needle.charAt(j)) 
                j = next[j - 1];//有冲突
            
            if (haystack.charAt(i) == needle.charAt(j)) 
                j++;
            
            if (j == m) 
                return i - m + 1;
            
        
        return -1;

之后的话就是Next数组的一个求法。这个我们先直接看到代码：

        int[] next = new int[m];
        for (int i = 1, j = 0; i < m; i++) 
            while (j > 0 && needle.charAt(i) != needle.charAt(j)) 
                j = next[j - 1]; // 有冲突回到前一位，然后对比那个所对应的下标为j的字符对不对得到
            
            if (needle.charAt(i) == needle.charAt(j)) 
            	//对得到加上1
                j++;
            
            next[i] = j;
        

这个代码其实不是好理解直接看的话，其实他这里是因为有一种规律在里面，假设我们现在next数组已经求好了。
他表示的含义呢我们前面也说了，表示的是这样的关系：

这个的话就是next数组里面不太好理解的地方，就是他是变求这个东西，边用这个东西。然后从左到右的一个计算，所有前面的值都是有的，也就是说能到。

理解不了的话，就记住嘛，也很好记，对得到j++,对不上j=next[j-1]
追不到，换一个妹子接着追，一直追不到，那一定是代码写错了