}
Posted 汀、
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了}相关的知识,希望对你有一定的参考价值。
相关文章:
数据挖掘机器学习---汽车交易价格预测详细版本[二]{EDA-数据探索性分析}
数据挖掘机器学习---汽车交易价格预测详细版本[三]{特征工程、交叉检验、绘制学习率曲线与验证曲线}
数据挖掘机器学习---汽车交易价格预测详细版本[四]{嵌入式特征选择(XGBoots,LightGBM),模型调参(贪心、网格、贝叶斯调参)}
数据挖掘机器学习---汽车交易价格预测详细版本[五]{模型融合(Stacking、Blending、Bagging和Boosting)}
数据挖掘机器学习[七]---2021研究生数学建模B题空气质量预报二次建模求解过程
码源+建模文章下载:见文末!!!
2021年中国研究生数学建模竞赛B题:空气质量预报二次建模
大气污染系指由于人类活动或自然过程引起某些物质进入大气中,呈现足够的浓度,达到了足够的时间,并因此危害了人体的舒适、健康和福利或危害了生态环境[1]。污染防治实践表明,建立空气质量预报模型,提前获知可能发生的大气污染过程并采取相应控制措施,是减少大气污染对人体健康和环境等造成的危害,提高环境空气质量的有效方法之一。
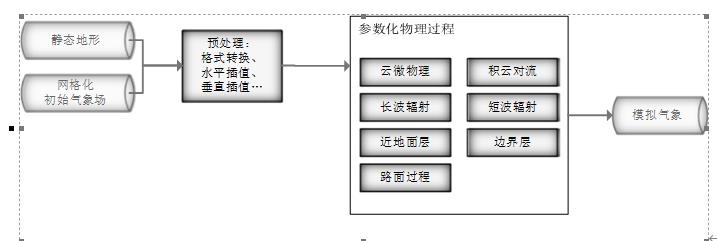
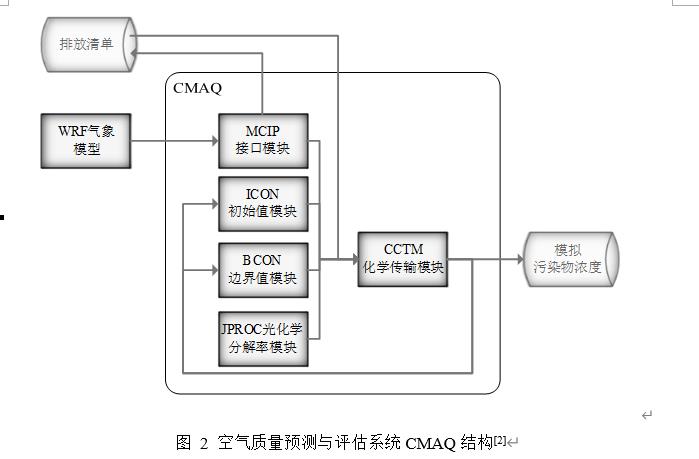
目前常用WRF-CMAQ模拟体系(以下简称WRF-CMAQ模型)对空气质量进行预报。WRF-CMAQ模型主要包括WRF和CMAQ两部分:WRF是一种中尺度数值天气预报系统,用于为CMAQ提供所需的气象场数据;CMAQ是一种三维欧拉大气化学与传输模拟系统,其根据来自WRF的气象信息及场域内的污染排放清单,基于物理和化学反应原理模拟污染物等的变化过程,继而得到具体时间点或时间段的预报结果。WRF和CMAQ的结构如图 1、图 2所示,详细介绍可以在附录提供的官网中进行查询
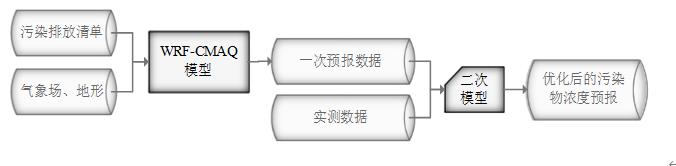
但受制于模拟的气象场以及排放清单的不确定性,以及对包括臭氧在内的污染物生成机理的不完全明晰,WRF-CMAQ预报模型的结果并不理想。故题目提出二次建模概念:即指在WRF-CMAQ等一次预报模型模拟结果的基础上,结合更多的数据源进行再建模,以提高预报的准确性。其中,由于实际气象条件对空气质量影响很大(例如湿度降低有利于臭氧的生成),且污染物浓度实测数据的变化情况对空气质量预报具有一定参考价值,故目前会参考空气质量监测点获得的气象与污染物数据进行二次建模,以优化预报模型。二次模型与WRF-CMAQ模型关系如图 3所示。为便于理解,下文将WRF-CMAQ模型运行产生的数据简称为“一次预报数据”,将空气质量监测站点实际监测得到的数据简称为“实测数据”。一般来说,一次预报数据与实测数据相关性不高,但预报过程中常会使用实测数据对一次预报数据进行修正以达到更好的效果。
问题1. 使用附件1中的数据,按照附录中的方法计算监测点A从2020年8月25日到8月28日每天实测的AQI和首要污染物,将结果按照附录“AQI计算结果表”的格式放在正文中。
问题2. 在污染物排放情况不变的条件下,某一地区的气象条件有利于污染物扩散或沉降时,该地区的AQI会下降,反之会上升。使用附件1中的数据,根据对污染物浓度的影响程度,对气象条件进行合理分类,并阐述各类气象条件的特征。
问题3. 使用附件1、2中的数据,建立一个同时适用于A、B、C三个监测点(监测点两两间直线距离>100km,忽略相互影响)的二次预报数学模型,用来预测未来三天6种常规污染物单日浓度值,要求二次预报模型预测结果中AQI预报值的最大相对误差应尽量小,且首要污染物预测准确度尽量高。并使用该模型预测监测点A、B、C在2021年7月13日至7月15日6种常规污染物的单日浓度值,计算相应的AQI和首要污染物,将结果依照附录“污染物浓度及AQI预测结果表”的格式放在论文中。
问题4. 相邻区域的污染物浓度往往具有一定的相关性,区域协同预报可能会提升空气质量预报的准确度。如图 4,监测点A的临近区域内存在监测点A1、A2、A3,使用附件1、3中的数据,建立包含A、A1、A2、A3四个监测点的协同预报模型,【联合】要求二次模型预测结果中AQI预报值的最大相对误差应尽量小,且首要污染物预测准确度尽量高。使用该模型预测监测点A、A1、A2、A3在2021年7月13日至7月15日6种常规污染物的单日浓度值,计算相应的AQI和首要污染物,将结果依照附录“污染物浓度及AQI预测结果表”的格式放在论文中。并讨论:与问题3的模型相比,协同预报模型能否提升针对监测点A的污染物浓度预报准确度?说明原因。---------要提升才行
具体word题目链接见:
2021年B题空气质量预报二次建模.zip-机器学习文档类资源-CSDN下载
1.基于Stacking机器学习混合模型的空气质量预测
摘 要:
大气污染系指由于人类活动或自然过程引起某些物质进入大气中,空气污染严重时,会对人体健康产生较大危害,空气质量指数(AQI)用来衡量空气质量状况,建立空气质量预报模型,预测可能发生的大气污染并采取相应控制措施,有利于减少大气污染对人体和环境等造成危害。
针对问题一、需要对原始数据进行简单的计算,原始数据来自于附件1中的监测点A从2020年8月25日到8月28日污染物浓度实测数据,这几天产生空气污染的首要污染物均为臭氧。
针对问题二、首先通过数据探索性分析对数据进行预处理,发现污染物分布符合无界约翰逊(Johnson SU)分布并做长尾截断处理,之后对数据进行归一化;其次通过相关性分析、顺序特征选择法(SFS)以及L1、L2正则化和弹性网络(ElaticNet)进行WRF-CMAQ预测气象特征进行筛选。随后对AQI进行动态分析,根据季节月份天数进行动态追踪分析,并采用聚类算法对气象分类进行验证,得到气象分类特征。
针对问题三、首先以A测试站点进行建模,根据筛选出来的气象特征和污染物变量特征;通过LGBM、Xgboots以及ElaticNet优化后的RNN和LSTM算法进行初次模型预测,同时采用贪心策略和贝叶斯网络对算法参数优化,衡量指标得到明显改善,其中分别以平平均绝对误差、均方根误差、MAPE 和R2作为模型评价指标,其次鉴于简单模型较难准确泛化各影响因素与空气质量之间的内在关系,文中进行Stacking方式将性能优秀的模型和WRF-CMAQ进行融合,并采用5折交叉验证的方法验证模型的预测能力。结果表明模型预测值和真实值一致性较强,且预测准确度很高,同时模型泛化能力很好适用于B、C检测站点。
针对问题四、考虑到A1、A2、A3、A4协同预报模型,在问题三构建的模型上着重考虑风速和风向特征因素带来的影响,以及考虑不同站点因为距离不同对A站点预测结果产生影响程度不同,进行权重配比构建基于Stacking融合的预测模型,结果表明风力因素对模型预测以及多站点协同预报对QAI以及污染物等预报更准确。
城市空气质量进行短期预测分析,最终实现对AQI指数具体值以及主要污染物成分的有效短期预测,克服当前监测系统后效性的缺陷,提供有效预警,,竭力为我市居民打造一个健康、可持续的居住环境具有更强的推广性。关键词: 空气质量预测,Stacking,Elastic Net-LSTM,LGBM,Xgboost
2.问题重述
2.1 问题背景
大气污染系指由于人类活动或自然过程引起某些物质进入大气中,呈现足够的浓度,达到了足够的时间,并因此危害了人体的舒适、健康和福利或危害了生态环境。污染防治实践表明,建立空气质量预报模型,提前获知可能发生的大气污染过程并采取相应控制措施,是减少大气污染对人体健康和环境等造成的危害,提高环境空气质量的有效方法之一。
目前常用WRF-CMAQ模拟体系(以下简称WRF-CMAQ模型)对空气质量进行预报。WRF-CMAQ模型主要包括WRF和CMAQ两部分:WRF是一种中尺度数值天气预报系统,用于为CMAQ提供所需的气象场数据;CMAQ是一种三维欧拉大气化学与传输模拟系统,其根据来自WRF的气象信息及场域内的污染排放清单,基于物理和化学反应原理模拟污染物等的变化过程,继而得到具体时间点或时间段的预报结果。WRF和CMAQ的结构如错误!未找到引用源。-1、错误!未找到引用源。所示,详细介绍可以在附录提供的官网中进行查询。
图1- 1中尺度数值天气预报系统WRF结构
但受制于模拟的气象场以及排放清单的不确定性,以及对包括臭氧在内的污染物生成机理的不完全明晰,WRF-CMAQ预报模型的结果并不理想。故题目提出二次建模概念:即指在WRF-CMAQ等一次预报模型模拟结果的基础上,结合更多的数据源进行再建模,以提高预报的准确性。其中,由于实际气象条件对空气质量影响很大(例如湿度降低有利于臭氧的生成),且污染物浓度实测数据的变化情况对空气质量预报具有一定参考价值,故目前会参考空气质量监测点获得的气象与污染物数据进行二次建模,以优化预报模型。
图1- 2空气质量预测与评估系统CMAQ结构
二次模型与WRF-CMAQ模型关系如错误!未找到引用源。所示。为便于理解,下文将WRF-CMAQ模型运行产生的数据简称为“一次预报数据”,将空气质量监测站点实际监测得到的数据简称为“实测数据”。一般来说,一次预报数据与实测数据相关性不高,但预报过程中常会使用实测数据对一次预报数据进行修正以达到更好的效果。
图1- 3 二次模型优化的WRF-CMAQ空气质量预报过程
根据《环境空气质量标准》(GB3095-2012),用于衡量空气质量的常规大气污染物共有六种,分别为二氧化硫(SO2)、二氧化氮(NO2)、粒径小于10μm的颗粒物(PM10)、粒径小于2.5μm的颗粒物(PM2.5)、臭氧(O3)、一氧化碳(CO)。其中,臭氧污染在全国多地区频发,对臭氧污染的预警与防治是环保部门的工作重点。臭氧浓度预报也是六项污染物预报中较难的一项,其原因在于:作为六项污染物中唯一的二次污染物,臭氧并非来自污染源的直接排放,而是在大气中经过一系列化学及光化学反应生成的(可参考附录 一种近地面臭氧污染形成机制 部分),这导致用WRF-CMAQ模型精确预测臭氧浓度变化的难度很高;同时,国内外已有的研究工作尚未得出臭氧生成机理的一般结论。
2.2 问题描述
需要通过建立数学模型,解决以下几个问题:
问题一: 计算AQI和首要污染物
根据附录中提供的计算方法,再利用附件1中的监测点A从2020年8月25日到8月28日每日实测数据来计算每日的实测AQI和首要污染物,并将计算得出的数据填入附录所给的“AQI计算结果表”中,再放到正文里。
问题二: 对气象条件进行合理分类
使用附件1中的数据,包括一次预报数据和实测数据,再根据对污染物浓度的影响程度,对气象条件进行合理分类,并阐述各类气象条件的特征
问题三: 建立二次预报数学模型
使用附件1、2中的数据,建立一个同时适用于A、B、C三个监测点的二次预报数学模型,用来预测未来三天6种常规污染物单日浓度值,要求二次预报模型预测结果中AQI预报值的最大相对误差应尽量小,且首要污染物预测准确度尽量高。并使用该模型预测监测点A、B、C在2021年7月13日至7月15日6种常规污染物的单日浓度值,计算相应的AQI和首要污染物,将结果依照附录“污染物浓度及AQI预测结果表”的格式放在论文中。
问题四: 建立区域协同预报模型
使用附件1、3中的数据,建立包含A、A1、A2、A3四个监测点的协同预报模型,要求二次模型预测结果中AQI预报值的最大相对误差应尽量小,且首要污染物预测准确度尽量高。使用该模型预测监测点A、A1、A2、A3在2021年7月13日至7月15日6种常规污染物的单日浓度值,计算相应的AQI和首要污染物,将结果依照附录“污染物浓度及AQI预测结果表”的格式放在论文中。并与问题3的模型相对比监测点A的污染物浓度预报准确度。
2.3模型假设
问题假设在问题求解过程中,考虑实际情况与简化计算的需求,提出了以下相关的假设:(1) 由于样本中数据缺失较多,假设在数据填充时,不会影响模型性能。
(2) 在变量筛选时,其他变量对模型预测性能无影响。
(3) 在有效信息提取和无用信息摒弃过程中对模型性能无影响。
(4) 所有样本数据都为实际场景的真实数据。
3、问题一模型的建立与求解
3.1 解题思路概述
问题1需要对原始数据进行简单的计算,原始数据来自于附件1中的监测点A从2020年8月25日到8月28日污染物浓度实测数据,由于原始数据只有四天的数据量,且没有数据缺失或异常,所以无需进行数据预处理。
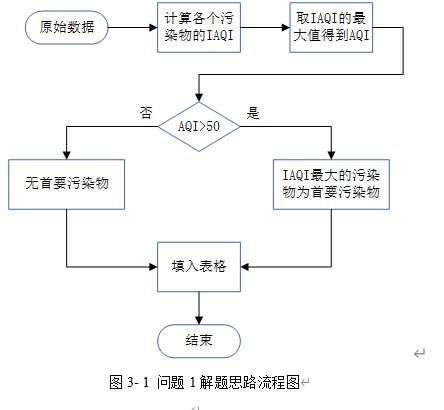
首先计算监测点A从2020年8月25日到8月28日的六项污染物的空气质量分指数(IAQI),取六个IAQI中的最大值得到空气质量指数(AQI),若AQI大于50,则IAQI最大的污染物为首要污染物。
确定问题一的总体思路如图3-1所示。
3.2 AQI的求解
3.2.1 计算各项污染物的IAQI
首先需得到各项污染物的空气质量分指数(IAQI),其计算公式如下:
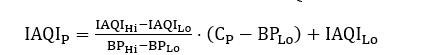
式中各符号含义如下:

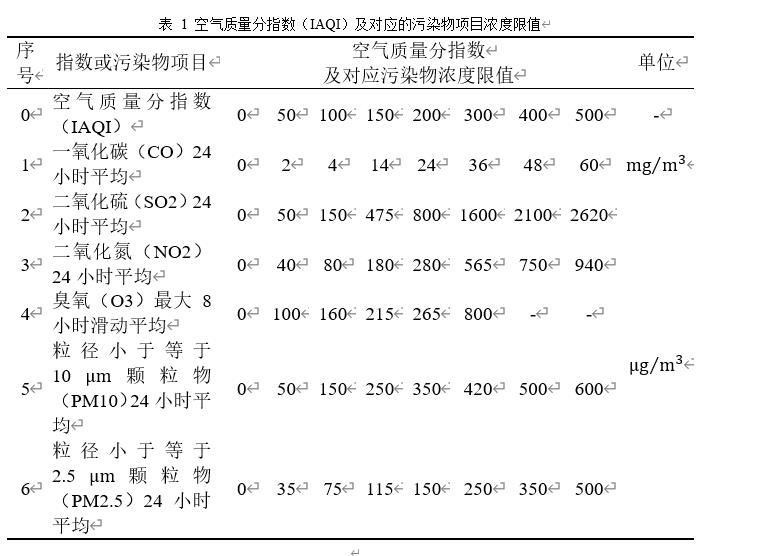
注:(1) 臭氧(O3)最大8小时滑动平均浓度值高于800 μg∕m^3 的,不再进行其空气质量分指数计算。
(2) 其余污染物浓度高于IAQI=500对应限值时,不再进行其空气质量分指数计算。
由于监测点A从2020年8月25日到8月28日污染物浓度实测数据均未到达限值,所以都进行空气质量分指数计算。
3.2.2 计算AQI计算首要污染物
在此模型中,对于AQI的计算仅涉及表 1提供的六种污染物,因此计算公式如下:

空气质量等级范围根据AQI数值划分,等级对应的AQI范围见表 2。

当AQI小于或等于50(即空气质量评价为“优”)时,称当天无首要污染物;
当AQI大于50时,IAQI最大的污染物为首要污染物。若IAQI最大的污染物为两项或两项以上时,并列为首要污染物。
IAQI大于100的污染物为超标污染物。
2020年8月25日到8月28日的AQI以及首要污染物的计算结果如表3所示:
表3 AQI计算结果表
4、数据预处理
由于数据表较多,且监测点A,B,C的预测和实测数据类型都相同,所以数据处理时论文只展现监测点A的预处理结果,对于其他的数据表,也采用相同的方法进行处理,便于问题2,3的模型建立。
4.1 缺失数据填充与处理
为了提高模型的能,一般会对数据进行预处理,因为数据预处理就是特征工程。通常,由于种种原因,在现实世界中,数据集有时会丢失缺失,例如传感器临时故障和其他人为错误。这些缺失的数据会降低模型的准确度,甚至有些缺失值的数据会让模型无法进行正确的预测。因此,应在建立模型之前填充数据。同时,数据中包含一些与预测特征无关的特征。为了提高模型的预测精度和建模效率,需要对模型的特征进行筛选。另外,不同数据特征的维度也是不同的,这就需要对数据进行标准化以提高模型的性能。
4.1.1 缺失数据分析
由于监测站点设备调试、维护等原因,监测站点的数据在连续时间内存在部分或全部缺失的情况,因此我们需要先对监测站点的数据进行分析,再确定对缺失数据的处理办法。如图所示的柱形图,可以直观的看到逐小时和逐日的缺失值,这样便于确定缺失的变量和它的值。
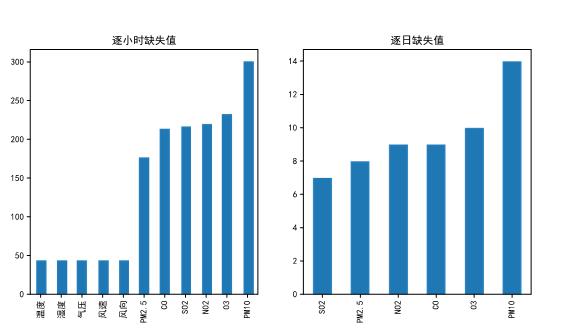
图4- 1 缺失值图
同时,再使用missingno可视化库对数据进行处理,得到缺失值无效矩阵图,无效矩阵是一个数据密集的显示,它可以快速直观地看出数据完整度。由图4-2和图4-3可知,空白越多说明缺失越严重,右侧的迷你图概述了数据完整性的一般形状,并指出了数据集中具有最大和最小无效值的行数。

图4- 2 逐小时监测数据缺失值无效矩阵图

图4- 3 逐日监测数据缺失值无效矩阵图
4.1.2 缺失数据处理
处理数据集中缺失值的方法主要有两种,一种是删除缺失值所在的行,另一种是填充缺失值。如果数据集中有很多缺失值的行,删除数据就会导致忽略一半以上的观察值,尤其是数据集较小时,会导致模型无法学习关键的数据分布,同时还会限值模型的性能。另外,当数据集是时间序列时,删除缺失值会导致模型无法学习相邻时间数据之间的关系。
本文使用多重插补的方法来填充缺失值,多重插补(Multiple Imputation)是一种基于重复模拟的处理缺失值的方法。它从一个包含缺失值的数据集中生成一组完整的数据集。
和单一插补不同的是,多重插补并没有试图去通过模拟值去估计每个缺失值, 而是提出缺失数据值的一个随机样本, 这种程序的实施恰当地反映了由于缺失值引起的不确定性, 使得统计推断有效。附件1的数据为气象数据,若简单的采用缺失值前后的数据进行填补,容易受到极端数值的影响,且缺失数据之间并不一定连续,如果使用多重填补在整体上进行一个缺失数据填充,能够让填充的数据更加的准确,更服从气象变化的规律。
多重插补推断包括了3个不同步骤:
(1)对缺失数据填补m次, 产生m个完整的数据集
(2)使用标准程序去分析这m个完整数据集
(3)综合这个完整数据集的结果, 用于推断
对于附件1中监测点A的逐小时和逐日的实测数据进行填充处理,采用多重插补的办法进行填充,最后得到无缺失值的数据集,如图4-4和图4-5所示,下面的缺失值无效矩阵图无空白处,右侧迷你图也没有突出的线,表明处理后的数据无缺失值。
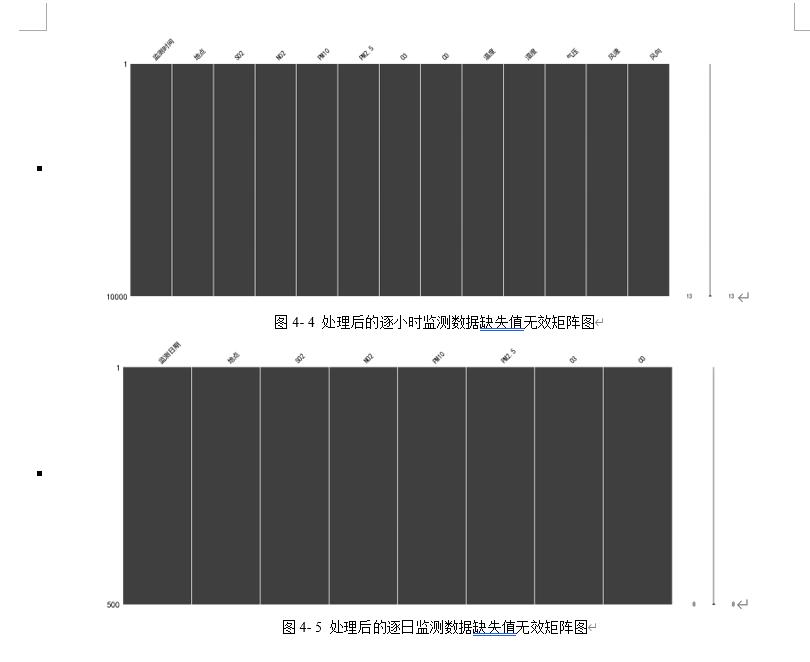
4.2 异常值分析
受监测站点及其附近某些偶然因素的影响,实测数据在某个小时或某天的数值偏离正常分布,这些偏离正常分布的值就为异常值,而这些异常值会影响模型的预测精度和准确度。异常值的定义是离其他数据点很远的点,对于很多统计算法来说,异常值会导致算法做出错误决策,严重干扰预测结果。但是,目前没有严格的统计规则来确定异常值,异常值检测只能依赖于学科领域的知识和对数据收集过程的理解。
异常值的监测方法有很多,例如箱形图、3-Sigma、长尾截断等。本文采用的异常值检测方法就是箱形图法。箱形图是用于显示一组数据分布信息的统计图表。以盒状形状得名。 主要用于反映原始数据分布的特征,也可以比较多个数据集的分布特征。箱线图提供了识别异常值的标准。异常值通常定义为小于 QL-k * QR或大于QU+k * QR的值。其中,QL为下四分位数,即所有观测值有四分之一比QL小,QU为上四分位数,所有观测值有四分之一比QU小。QR是四分位距,即上四分位数QU和下四分位数QL之间的差值。本文的k值使用默认的k值3。图4-6的左图是逐日的〖SO〗_2监测浓度的原数据的箱形图,右图是使用箱形图剔除异常值后的箱形图,其中黑色的点是异常值,由图可以看出,清除异常值的效果非常显著,左图的大量异常值清除到只剩右图的一个异常值,仅剩的一个异常值对于模型预测的准确度影响不大,可以不再进行删除处理。

图4- 6 处理前后的SO2箱形图
使用箱形图对所有数据进行异常值删除处理,得到图-,由图4-7可知,部分污染物仍然存在少量的异常值,少量的异常值对于预测模型的影响不大,若将其删除,可能也会对后续的预测造成较大的影响,所以不再进行删除处理。
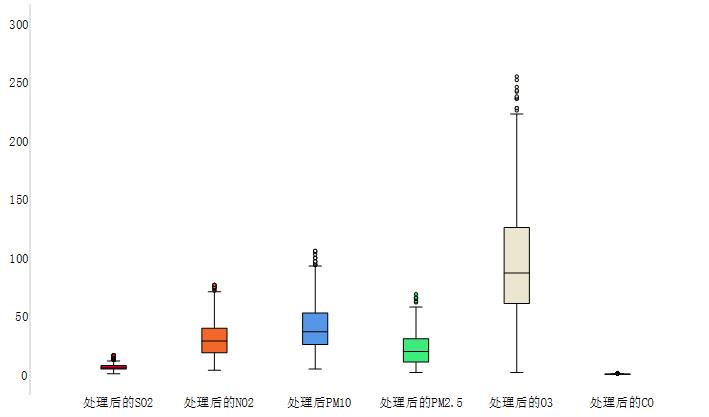
图4- 7 各种污染物处理后的浓度的箱形图
4.3 描述性统计分析
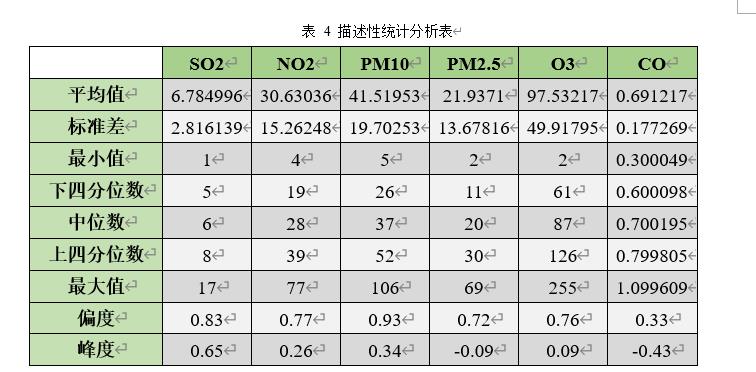
描述性统计分析是将一系列复杂的数据减少到几个能起到描述作用的关键数字,是对已有数据集的一个整体情况描述,主要体现数据的集中趋势和离散趋势。描述性统计分析包含平均值、标准差、最小值、下四分位数、中位数、上四分位数、最大值、偏度、峰度等关键数值,通过平均值和上下四分位数,可以比较好的描述数据的整体分布情况,通过标准差、中位数、偏度、峰度,可以反映出数据波动的程度和识别出可能的异常值。描述性统计分析如表4所示
表 4 描述性统计分析表
偏度(Skewness)可以用来度量随机变量概率分布的不对称性。公式为:
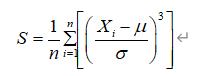
其中μ是均值,δ是标准差。偏度的取值范围为(-∞,+∞)。当偏度<0时,概率分布图左偏。当偏度=0时,表示数据相对均匀的分布在平均值两侧,不一定是绝对的对称分布。当偏度>0时,概率分布图右偏。
峰度可以用来度量随机变量概率分布的陡峭程度。公式为:
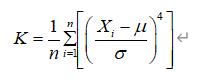
其中μ是均值,δ是标准差。完全服从正态分布的数据的峰度值为 0,峰度值越大,概率分布图越高尖,峰度值越小,越矮胖。
通过表可以看出,全部数据的偏度都大于0,所以全部数据均右偏,PM2.5和O_3的峰度比较靠近0,所以分布比较接近正态分布,其余偏离正态分布的程度都较大,特别是〖SO〗_2,因此需要在下文中对数据进行数据分布分析,把偏离正态分布的数据进行变换使其符合正态分布。
4.4 数据分布分析
对数据进行数据分布分析可以得到对应数据的分布特征和分布类型,分析完成得到数据的分布后,可以根据数据的不同分布对数据进行不同的预处理。例如,若数据服从正态分布:根据正态分布的定义可知,距离平均值3δ之外的概率为 P(x-μ>3δ) <= 0.003 ,这属于极小概率事件,在默认情况下我们可以认定,距离超过平均值3δ的样本是不存在的。因此,当样本距离平均值大于3δ,认为该样本为异常值,所以可以使用3-Sigma准则筛选掉一些异常值。图4-8为逐日的部分污染物浓度数据的数据分布。
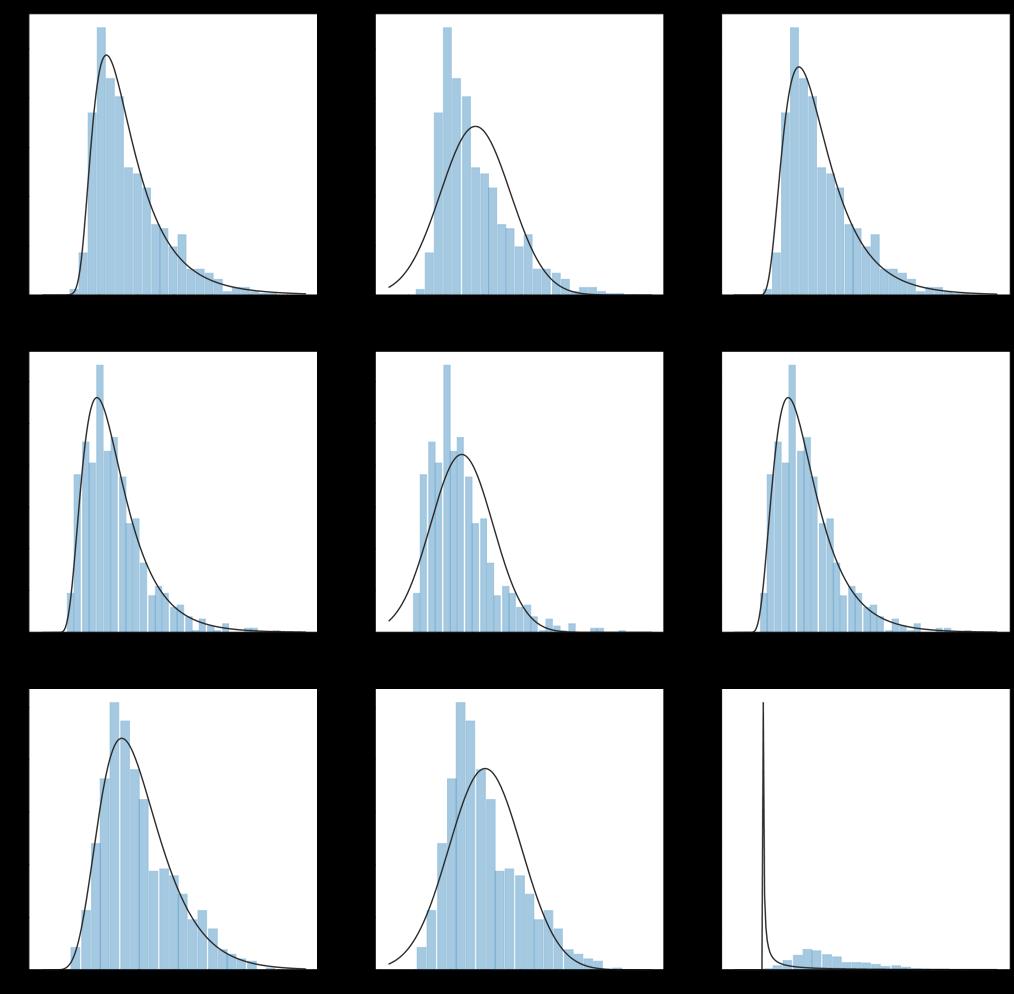
图4- 8 PM10、NO2、O3的三种分布图
由图4-8可知,PM10和〖NO〗_2均符合无界约翰逊(Johnson SU)分布和log正态分布,不符合正态分布;O_3符合无界约翰逊分布和正态分布,不符合log正态分布。〖SO〗_2、PM2.5、CO和PM10以及〖NO〗_2一样,均符合无界约翰逊分布和log正态分布,不符合正态分布,分布图在附录图中进行展示。
对于不符合正态分布的数据,对其进行Johnson变换或log变换,使数据变换后服从正态分布。
4.5 数据标准化和归一化
标准化和归一化都是指特征工程中的特征缩放过程,特征缩放的作用是:
1.使不同量纲的特征处于同一数值量级,减少方差大的特征的影响,使模型更准确。
2.加快学习算法的收敛速度。
本文采用的数据归一化方法为最大最小值标准化方法,如公式所示:
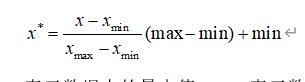
x表示原本的数据,x_max表示数据中的最大值,x_min表示数据中的最小值,max和min分别是期望放缩的每一列特征之间的最大值和最小值。换句话说,就是将每一列的特征放缩到min到max之间,这种缩放减少了异常值的权重,但作为一个副作用,标准偏差太小以至于在某些模型中可能没有用。通常,如果数据不是正态分布的,则使用最小值-最大值标准化方法对数据进行归一化。在这篇论文中,max设置为 1,min设置为0.001,样本的特征值线性映射到 [0.001, 1]。
标准化是将数据变换为均值为0,标准差为1的标准正态分布,本质上,标准化和归一化的作用一样,都是将将原始的一列数据转换到某个范围,或者某种形态。标准化方法有均值标准化和0-1标准化,通常使用的标准化方法为0-1标准化,标准化方程为:
其中μ是均值,δ是标准差。
5、特征变量筛选
数据经过预处理后,需要选择有意义的特征并输入机器学习算法和模型进行训练。一般来说,选择特征有两个方面的考虑:
(1)特征是否发散:如果特征不发散,比如方差接近于0,也就是这个特征的样本之间本质上没有区别,这个特征对区分样本没有帮助。
(2)特征与目标的相关性:这更明显。首先应该优先考虑与您的目标最相关的功能。除方差法外,本文中介绍的所有其他方法均考虑相关性。
根据特征选择的形式又可以将特征选择方法分为3种:过滤法(Filter)、包裹法(Wrapper)、嵌入法(Embedded)。
5.1 过滤法
5.1.1斯皮尔曼等级相关系数
过滤法按照发散性或者相关性对各个特征进行评分,设定阈值或者待选择阈值的个数,选择特征。本文采用两种过滤式的方法进行特征筛选:斯皮尔曼法和方差选择法。
斯皮尔曼法:斯皮尔曼等级相关系数是一种用于评估两个变量之间相关性的统计方法,其特点是无需调查样本量或变量的整体分布特征,具有快速、稳健的特征。对于维度为n的两个向量X和Y,X_i、Y_i分别表示它们对应的 i (1≤i≤n) 个元素。X和Y按同样的方式升序或降序排列,得到一个新的变量序列x,y.,其中元素x_i为X_i在X中的秩,y_i为Y_i在Y中的秩。相应地,得到差集d_i=x_i-y_i并定义随机变量X和Y之间的斯皮尔曼等级相关系数如下:
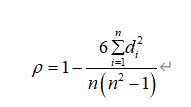
式中:n为数列点数,对应于一个窗长的采样点数;ρ为斯皮尔曼等级相关系数。分子是两个序列之间的误差之和,反映了两个变量之间的差异。分母是与序列长度相关的常数。计算过程表明,斯皮尔曼等级相关系数计算效率高,限制因素少。
5.1.2方差选择法
就是针对每一列特征X,求其方差,然后通过设定一个阈值,来选取方差较大的特征,方差大说明信息量大。
使用斯皮尔曼法进行一次特征选择后可得到图5-1、图5-2、图5-3。

图5- 1 预测数据的相关性热力图
综上空气质量的好坏与季节及气象条件的关系十分密切。在污染物排放相对稳定的情况下,气象条件对AQI起着十分重要的作用。本文选取温度、湿度、气压、风速与风向五个气象条件进行相关分析,探寻气象条件与AQI之间的关系,得出AQI与各月气象因子相关系数。
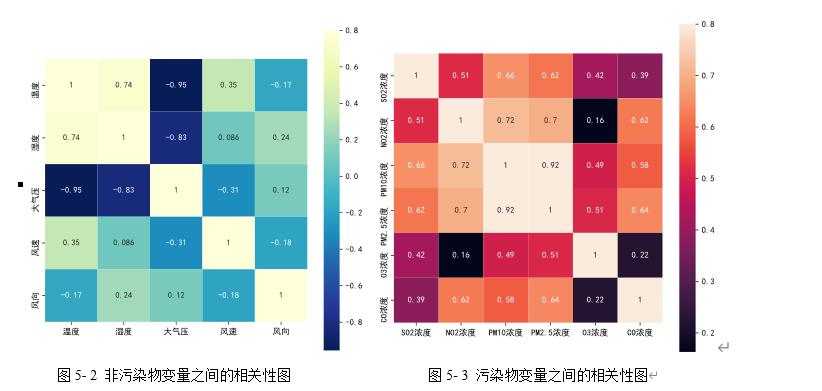
图5- 2 非污染物变量之间的相关性图 图5- 3 污染物变量之间的相关性图
由相关性热力图可直观看出不同的数据表的变量之间的相关性。比如在图-和图-,大气压和温度的交点图是黑色的,表明大气压和温度之间的相关性很高;在图-中,PM10和PM2.5的相关系数高达0.92,表明PM10和PM2.5之间的相关性很高。
5.2 包裹法
5.2.1 顺序特征选择法SFS
包裹法根据目标函数(通常是预测效果评分),每次选择若干特征,或者排除若干特征。本文使用顺序特征选择法(Sequential feature selection,SFS)进行特征筛选。
顺序特征选择算法是一系列贪婪搜索算法,用于将初始d维特征空间缩减为k维特征子空间,其中k<d。特征选择算法背后的动机是自动选择与问题最相关的特征子集。这通过移除不相关的特征或噪声来提高计算效率或降低模型的泛化误差,这对于不支持正则化的算法可能很有用。该算法可以以两种方式之一工作,即向前(SFS)或向后(SBS)。SFS中,算法从只使用其中一个特征开始,并尝试使用给定的模型对数据建模。然后,它选择提供最高精度或一组性能指标的功能。此过程会重复进行,直到用户决定一定数量的功能。SBS向后工作,这意味着它从所有功能开始,删除性能降幅最小的功能。这会重复到一定数量的功能。为了确保已覆盖所有组合,还可以包括或删除先前拾取的功能。这些变化被称为用于向前移动的顺序向前浮动选择(SFFS)或用于向后移动的顺序向后浮动选择(SBFS)。
分别使用SFS进行两次特征选择,得到两次特征序列图和表,图5-4为第一次特征选择序列图,图5-5为第二次特征选择序列图,表为第一次特征选择序列表,表第二次特征选择序列表。
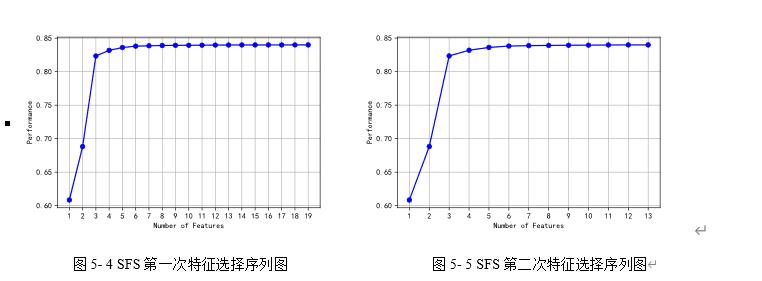
图5- 4 SFS第一次特征选择序列图 图5- 5 SFS第二次特征选择序列图
表 5 SFS第一次特征选择序列表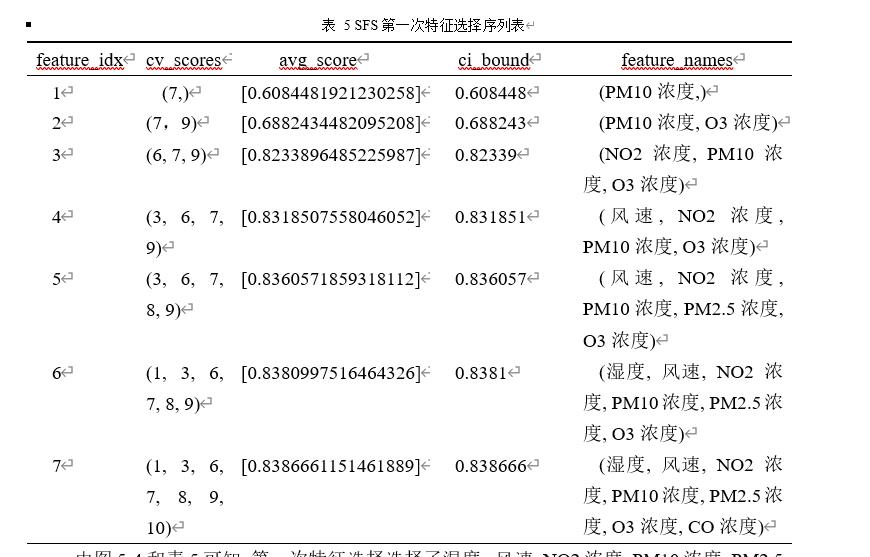
由图5-4和表5可知,第一次特征选择选择了湿度, 风速, NO2浓度, PM10浓度, PM2.5浓度, O3浓度, CO浓度,其中PM10浓度的权重最高。
表 6 SFS第二次特征选择序列表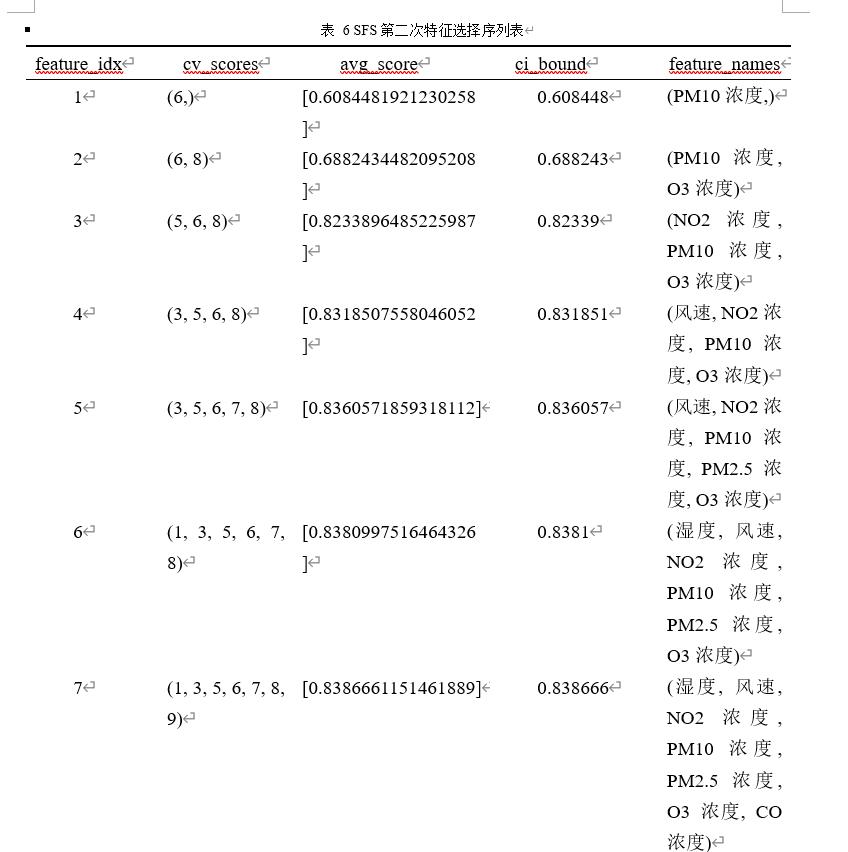
由图5-5和表6可知,第二次特征选择同样选择了湿度, 风速, NO2浓度, PM10浓度, PM2.5浓度, O3浓度, CO浓度,其中还是PM10浓度的权重最高。
5.3 嵌入法
嵌入法先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据系数从大到小选择特征。类似于Filter方法,但是是通过训练来确定特征的优劣。本文使用基于惩罚项的特征选择法和随机森林算法,其中基于惩罚项的特征选择法分为L1惩罚项、L2惩罚项和(L1+L2)惩罚项。
5.3.1 基于Lasson回归特征选择法
使用L1正则化的模型叫做Lasson回归,Lasson回归是一种可以客观筛选有效变量,解决多重共线性等问题的估计方法。将惩罚项添加到回归系数的绝对值之和,以最小化回归模型的残差平方和。然后筛选等于零的回归系数。解决模型的多重共线性问题。
LASSO 回归的核心是在普通线性回归的基础上添加𝐿1惩罚项,即:
使用Lasson回归算法进行两次特征选择,得到特征筛选后的结果。如图5-6和图5-7所示。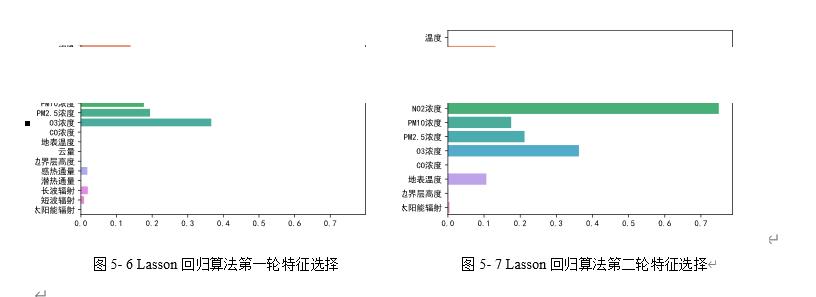
图5- 6 Lasson回归算法第一轮特征选择 图5- 7 Lasson回归算法第二轮特征选择
由图5-6可知,第一次特征选择选择了湿度、风向,SO2浓度,NO2浓度,PM10浓度,PM2.5浓度,O3浓度,感热通量,长波辐射,短波辐射,其中NO2浓度的权重最高。由图5-7可知,第二次特征选择选择了湿度,大气压,风速,SO2浓度,NO2浓度,PM10浓度,PM2.5浓度,O3浓度,地表温度,太阳能辐射,其中NO2浓度的权重还是最高的。
5.3.2 基于Ridge回归特征选择法
使用 L2 正则化的模型叫做Ridge回归,Ridge回归的损失函数为:
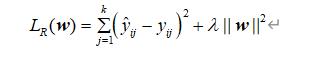
Ridge回归是一种专用于共线性数据分析的偏差估计回归方法。这本质上是最小二乘法的改进,但是通过以丢弃一些信息和准确性为代价丢弃最小二乘法的偏差,让功能模型变得更加可靠并且模型提高了数据适用性。
使用Ridge回归算法进行两次特征选择,得到特征筛选后的结果。如图5-8和图5-9所示。
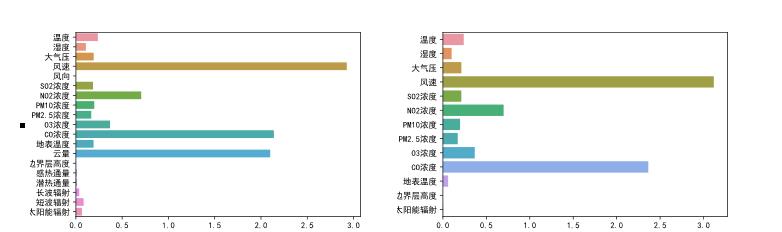
图5- 8 Ridge回归第一轮特征选择 图5- 9 Ridge回归第二轮特征选择
由图5-8可知,第一次特征选择选择了温度,湿度,大气压,风速,SO2浓度,NO2浓度,PM10浓度,PM2.5浓度,O3浓度,CO浓度,地表温度,云量,长波辐射,短波辐射,太阳能辐射,其中风速的权重最高。由图5-9可知,第二次特征选择选择了温度,湿度,大气压,风速,SO2浓度,NO2浓度,PM10浓度,PM2.5浓度,O3浓度,地表温度,其中风速的权重还是最高的。
5.3.3 基于ElasticNet特征选择法
带(L1+L2)惩罚项的算法是ElasticNet算法, ElasticNet 算法是一种线性回归模型,它使用 L1 和 L2 范数作为正则化矩阵。这种方法的优点是既保留了LASSO方法容易出现特征稀疏的特点,也在循环的过程中继承了Ridge回归 L2 正则化的稳定性。算法公式如下:
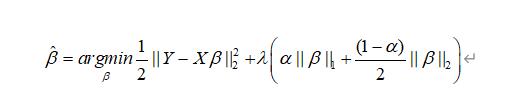
其中,λ表示惩罚系数,β表示回归系数。 对于L1和L2正则化的凸组合(即公式中的α的取值),调整l1_ratio参数,通过十折交叉验证的方式选择模型误差中最小值的参数值来选择参数的最终值。
5.3.4 随机森林
随机森林是在bagging算法的基础之上改动演化过来的。bagging算法是在原始的数据集上采用有放回的随机取样的方式来抽取 个子样本,从而利用这 个子样本训练 个基学习器,从而降低了模型的方差。
随机森林的改动有两处,第一:不仅随机的从原始数据集中随机的抽取 个子样本,而且在训练每个基学习器的时候,不是从所有特征中选择最优特征来进行节点的切分,而是随机的选取k个特征,从这k个特征中选择最优特征来切分节点,从而更进一步的降低了模型的方差;第二:随机森林使用的基学习器是CART决策树。
随机森林随机选择的样本子集大小m越小模型的方差就会越小,但是偏差会越大,所以在实际应用中,一般会通过交叉验证的方式来调参,从而获取一个合适的样本子集。
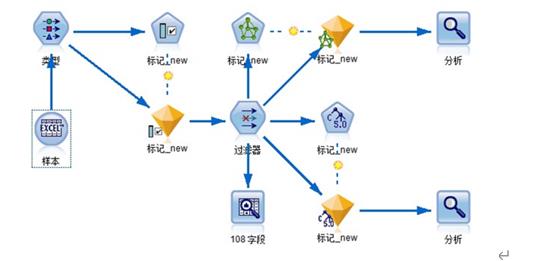
图5- 10 神经网络、随机森林模型
使用随机算法进行两次特征选择,得到特征筛选后的结果。如图5-11和图5-12所示。
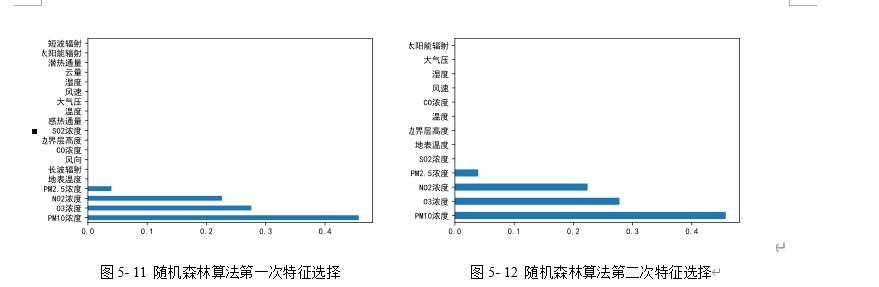
图5- 11 随机森林算法第一次特征选择 图5- 12 随机森林算法第二次特征选择
由图5-11可知,第一次特征选择选择了PM2.5浓度,NO2浓度,O3浓度,PM10浓度,其中PM10浓度的权重最高。由图5-12可知,第二次特征选择同样选择了PM2.5浓度,NO2浓度,O3浓度,PM10浓度,其中PM10浓度的权重还是最高的。
5.3.5 小结
综上所述,NO2、O3浓度,PM10浓度,PM2.5浓度,温度,湿度,大气压,风速,地表温度等为特征变量
6、问题二的模型建立与求解
6.1 解题思路概述
问题2为分类问题,该题要求使用附件1中的监测点A的一次预报数据和实测数据,再根据对污染物浓度的影响程度,对气象条件进行合理的分类。
(3)季节划分方法。参照气象学季节划分方法,将四季划分为春季(3-5月)、夏季(6-8月)、秋季(9-11月)、冬季(12月至次年2月)。
6.2 AQI的动态分析
根据《环境空气质量指数(AQI)技术规定(试行)》(HJ633-2012)标准,利用2019.04-2021.07的AQI逐日数据,进行分级统计,得到不同等级天数的分布情况。
6.2.1 AQI的天数变化
为了进一步详细地分析AQI的状况,我们分析了2019年六月份到2021年7月份内每天的AQI。逐日的AQI如图6-1所示
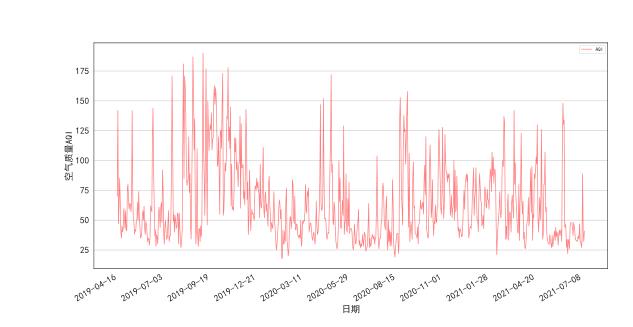
图6- 1 逐日AQI变化
分析结果显示,AQI的总体状况较好,波动范围主要集中在50至125之间,平均AQI达到一级优的天数为146天,占总天数的43.2%;二级良的天数为125天,占总天数的37.0%;三级轻度污染的天数为38天,占总天数的11.2%,其它(重度污染、严重污染)的总共占总天数的8.6%。
6.2.2 AQI的逐小时变化
此外,根据六种污染物的逐小时的变化情况计算得到AQI的逐小时变化的趋势如图6-2所示
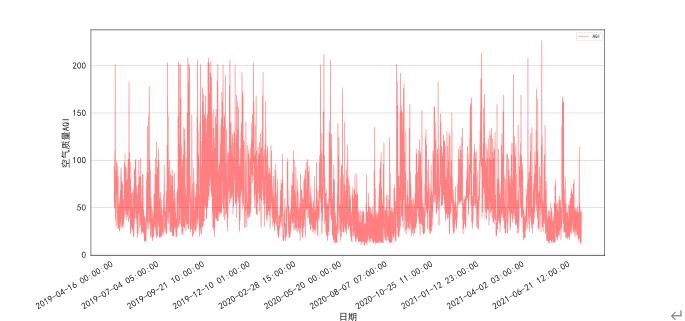
图6- 2 逐小时AQI变化
图2的开始日期与结束日期分别为2019年4月16日零点、2021年7月13日七点。其变化趋势与AQI的逐天数变化趋势(图1)大致相同。
6.2.3 AQI的月份变化
基于新的AQI的新计算方法,详细分析了从2019年4月份到2021年七月份的AQI逐月变化动态。如图6-3所示,AQI总体状况较好。出现频率最高的空气质量等级为一级优与二级良;其次为三级轻度污染;再其次为四级中度污染;另外五级重度污染与六级严重污染几乎从来没有出现。
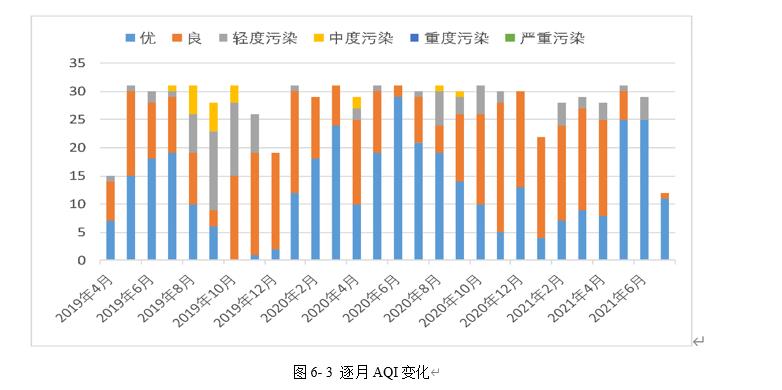
图6- 3 逐月AQI变化
另外,为了更合理的分析每个月份的AQI变化动态,将2019年四月份到2021年七月份中相同月份的AQI数据进行了合并取均值得到了图6-4。从图6-4中可以看出每个月份中空气质量各等级的大致占比,一级优在每年的五月份到七月份占比最高,依次为63.5%、80.0%、69.9%;一级优在每年的十月份到十二月份占比最少,依次为16.1%、10.7%;三级轻度污染与四级中度污染主要集中在八月份到十一月份,占比依次为30.6%、39.9%、33.9%、16.1%;
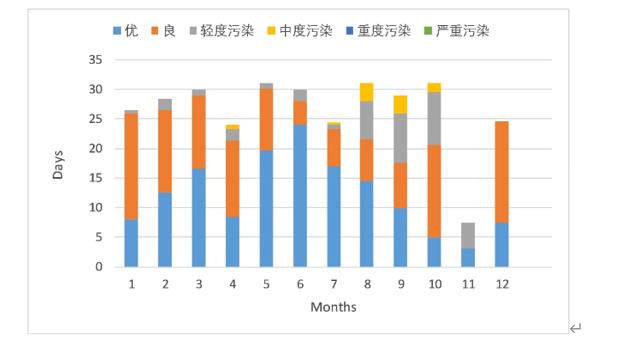
图6- 4 相同月份的AQI数据
由2019到2021AQI和IAQI的月变化图如图6-5所示,AQI的峰值和谷值分别出现在6月和 10月,其分别为42与88。总体来说,AQI与IAQI在5到7月保持较低的状态,在9到11月保持较高的状态。
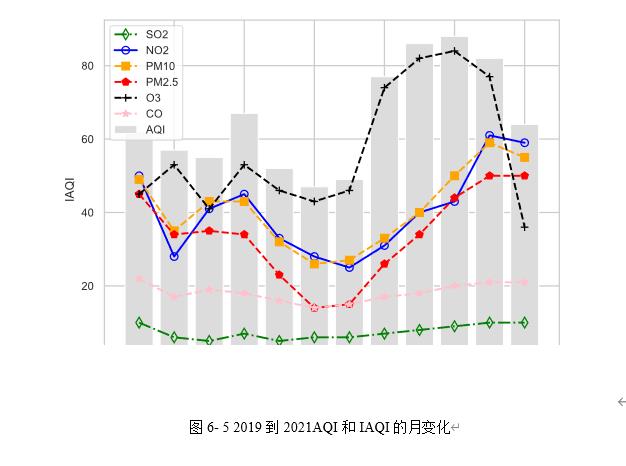
图6- 5 2019到2021AQI和IAQI的月变化
6.2.4 AQI的季节变化
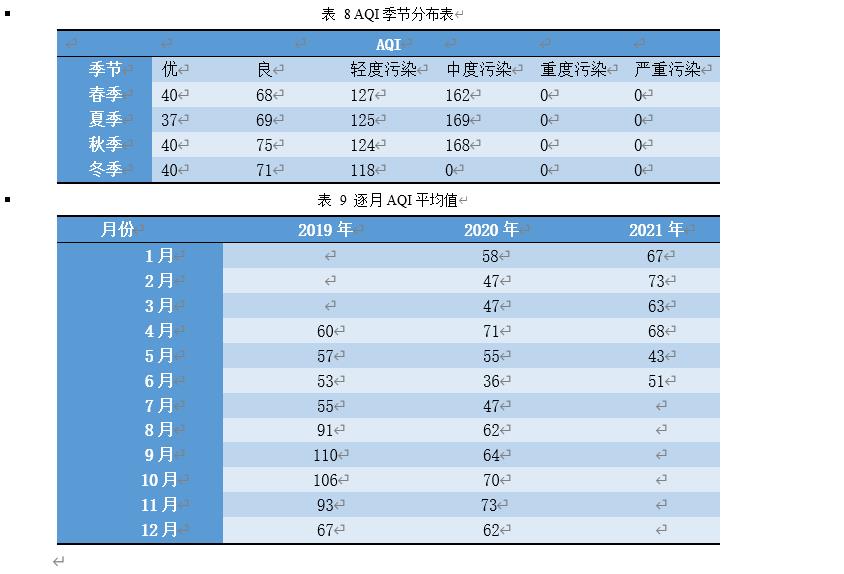
6.3 聚类分析
该部分对2019年4月份到2021年7月份间的日均空气质量AQI指数进行聚类分析,以得到这两年的AQI指数是否有明显的季节趋势。该数据单位一致,故不需要标准化处理,对这两年各月份的日均AQI求均值,将各年的日均AQI数值汇总为月度数据,结果如下表所示
将表中的12个月份作为聚类分析的12个指标输入SPSS进行聚类分析,得到聚类图形。
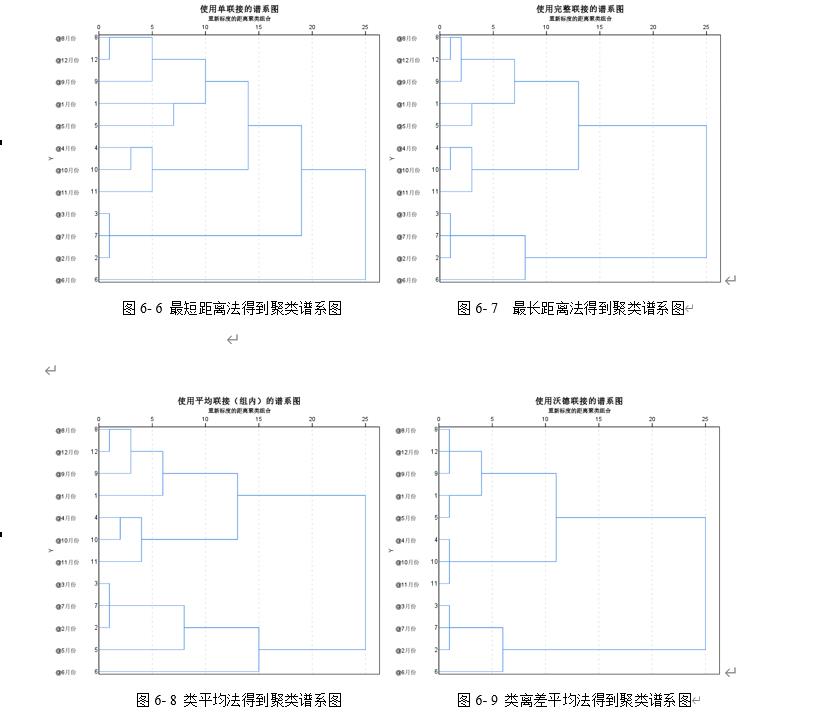
6.4 结果分析
综上所述,由上述四种不同分类准则的系统聚类方法结果可以看出,通过月份分析,2019年6月到2021年7月的AQI走势是有明显的季节趋势。从四种不同的准则下的聚类图可以明显的看出,9月和10月的AQI最高,空气污染程度最严重;4月和11月的AQI较高,空气污染较为严重;其它月份污染程度较轻。
7、问题三的模型建立与求解
7.1 问题分析
首先以A测试站点进行建模,根据筛选出来的气象特征和污染物变量特征;通过LGBM、Xgboots以及ElaticNet优化后的RNN和LSTM算法进行初次模型预测,同时采用贪心策略和贝叶斯网络对算法参数优化,衡量指标得到明显改善,其中分别以平平均绝对误差、均方根误差、MAPE 和R2作为模型评价指标,其次鉴于简单模型较难准确泛化各影响因素与空气质量之间的内在关系,文中进行Stacking方式将性能优秀的模型和WRF-CMAQ进行融合,并采用5折交叉验证的方法验证模型的预测能力。结果表明模型预测值和真实值一致性较强,且预测准确度很高,同时模型泛化能力很好适用于B、C检测站点。
图7-1 天气循环图

图7-2 模型预测流程图
7.2 模型评价指标
本文采用以下四个指标来评价所涉及空气质量预测模型的性能,分别是平均绝对误差(Mean Absolute Error,MAE)、均方根误差(Root Mean Square Error,RMSE)、MAPE 和决定系数(Coefficient of Determination,R2),计算过程如公式、公式、公式和公式所示。
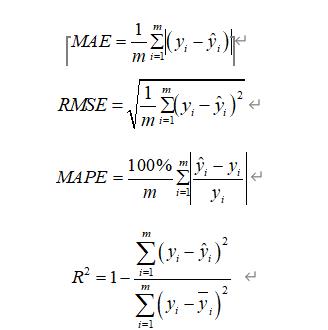
其中,m为样本大小,y_i为模型的实际观测值, 为模型的预测值, 为实际观测值的平均值。一般来说,RMSE和MAE值越小,模型越准确。MAE为绝对误差,适用于预测值与实际观测值误差比较明显的情况。误差越大,权重越大。RMSE适用于预测误差不是很明显的情况。RMSE等价于2个范数,对离散点更敏感。与RMSE相比,MAPE对单个离散点不那么敏感,并且更加稳健。但是MAPE的分母不能为0,否则计算结果将是无穷大的,毫无意义。 R2 是一个综合度量,用于衡量每个自变量对因变量变化的解释程度。 R2越接近1,对变量的解释越强,其值越接近0,解释越弱。
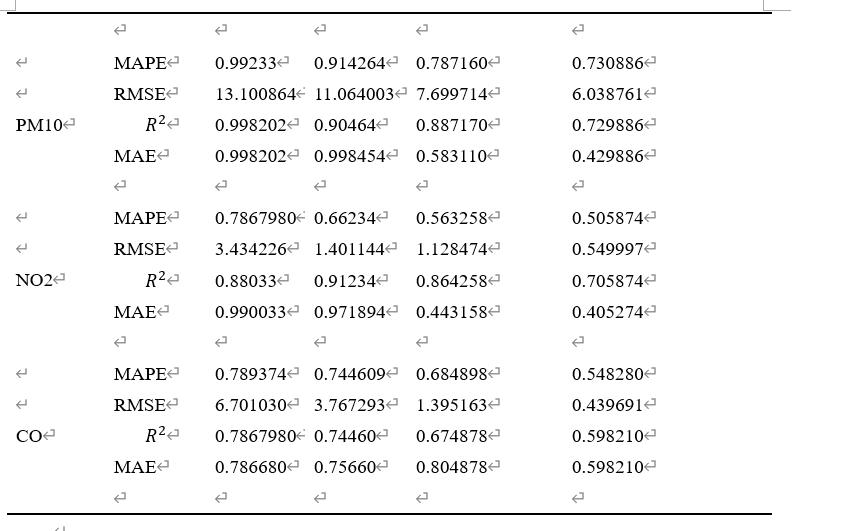
表 10单变量空气质量预测结果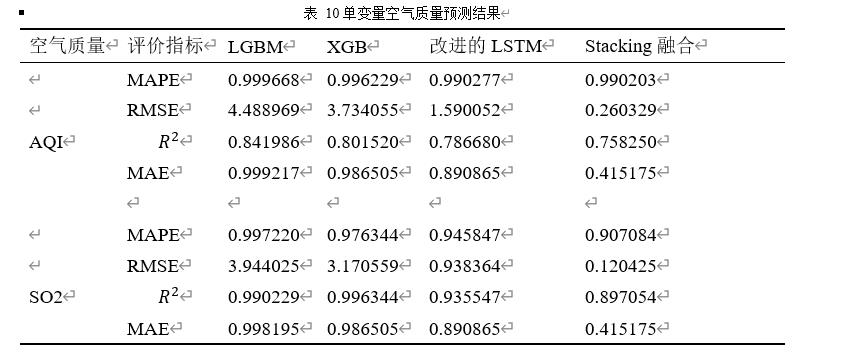
7.3 预测模型
7.3.1 LGBM
GBDT (Gradient Boosting Decision Tree) 是机器学习中一个长盛不衰的模型,其主要思想是利用弱分类器(决策树)迭代训练以得到最优模型,该模型具有训练效果好、不易过拟合等优点。而LightGBM(Light Gradient Boosting Machine)是一个实现GBDT算法的框架,支持高效率的并行训练,并且具有更快的训练速度、更低的内存消耗、更好的准确率、支持分布式可以快速处理海量数据等优点。LightGBM提出的主要原因就是为了解决GBDT在海量数据遇到的问题,让GBDT可以更好更快地用于工业实践。LightGBM的基本原理为基于Histogram的决策树算法、深度限制的 Leaf-wise 算法和和单边梯度采样算法。LGBM的优点为互斥特征捆绑、带深度限制的Leaf-wise的叶子生长策略、支持类别特征、支持高效并行与Cache命中率优化。
7.3.2 Xgboost
XGBoost是一套提升树可扩展的机器学习系统。XGBoost的核心算法思想不难,,大致如下:
(1)添加树,不断地进行特征分裂来生长一棵树,每次添加一个树,其实是学习一个新函数f(x),去拟合上次预测的残差。
(2) 当我们训练完成得到k棵树,我们要预测一个样本的分数,其实就是根据这个样本的特征,在每棵树中会落到对应的一个叶子节点,每个叶子节点就对应一个分数
(3)需要将每棵树对应的分数加起来就是该样本的预测值。
主要创新点为:设计和构建高度可扩展的端到端提升树系统、提出了一个理论上合理的加权分位数略图(weighted quantilesketch )来计算候选集、引入了一种新颖的稀疏感知算法用于并行树学习。 令缺失值有默认方向与提出了一个有效的用于核外树形学习的缓存感知块结构。 用缓存加速寻找排序后被打乱的索引的列数据的过程。
7.3.3 RNN
RNN(Recurrent Neural Network),中文称作循环神经网络,一般以序列数据为输入,通过内部的结构设计有效捕捉序列之间的关系特征,一般也是以序列形式进行输出。
RNN的循环机制使模型隐层上一时间步产生的结果, 能够作为当下时间步输入的一部分(当下时间步的输入除了正常的输入外还包括上一步的隐层输出)对当下时间步的输出产生影响。
7.3.4 LSTM
LSTM神经网络是循环神经网络的一种,与1997年被Hochreiter等人在RNN神经网络的基础上研究而出。LSTM神经网络因其内在阀门设计的特点,能够高效应用在时间序列数据,特别是时间依赖型时间序列数据。根据前人的研究成果不难得出,LSTM神经网络相较于传统神经网络拥有更强的数据拟合性,势必在股票市场数据分析中绽放出更璀璨的光芒。LSTM神经网络是RNN循环网络
以上是关于}的主要内容,如果未能解决你的问题,请参考以下文章