优化器算法optimizer

Posted 2022-12-14 AI蜗牛之家

文章目录

• 1.相关背景
• • 1.1.指数加权移动平均(Exponential Weighted Moving Average)
  • • 1.1.1.演化与概述
    • 1.1.2.公式理解
    • 1.1.3.EMA 偏差修正
    • 1.1.4.EMA 在 Momentum 优化算法中应用的理解
• 2.递归下降算法
• • 2.1.BGD MBGD SGD
  • 2.2.Momentum
  • 2.3.Nesterov Accelerated Gradient
  • 2.4 Adagrad
  • 2.5.Adadelta
  • 2.6 RMSProp
  • 2.7 Adam
  • 2.8 如何选择优化算法
• 其他相关优化方法
• 参考链接

其实本来是没有想写关于optimizer的，因为网上的一搜一大把，但是我发现好多文章都讲的乱七八糟，可能可能知道相关概念的人来看就比较顺畅，但是对于小白或者是之前接触比较少的人来说，就比较费劲，我这里也是作为自己的笔记，重新梳理一下，多数资料也是来源于之前的大牛blog，最后会有相关参考链接

1.相关背景

1.1.指数加权移动平均(Exponential Weighted Moving Average)

1.1.1.演化与概述

算术平均（权重相等）—>加权平均（权重不等）—>移动平均（大约是只取最近的 N 次数据进行计算）—> 批量归一化(BN)及各种优化算法的基础
EMA：是以指数式递减加权的移动平均，各数值的加权影响力随时间呈指数式递减，时间越靠近当前时刻的数据加权影响力越大

1.1.2.公式理解

• $v_t=\beta v_{t-1}+(1-\beta ){\theta }_t$，公式中 ${\theta }_t$ 为 t 时刻的实际温度；系数 \\beta 表示加权下降的快慢，值越小权重下降的越快；$v_t$ 为 t 时刻 EMA 的值。
• 当 $v_0=0$ 时，可得：$$v_t=(1-\beta )({\theta }_t+\beta {\theta }_{t-1}+{\beta }^2{\theta }_{t-2}+...+{\beta }^{t-1}{\theta }_1)$$，从公式中可以看到：每天温度($\theta$)的权重系数以指数等比形式缩小，时间越靠近当前时刻的数据加权影响力越大。
• 在优化算法中，我们一般取 $\beta >=0.9$，而 $1+\beta +{\beta }^2+...+{\beta }^{t-1}=\frac{1-{\beta }^t}{1-\beta }$，所以当 t 足够大时 ${\beta }^t\approx 0$，此时便是严格意义上的指数加权移动平均。
• 在优化算法中，我们一般取 $\beta >=0.9$，此时有 ${\beta }^{\frac{1}{1-\beta }}\approx \frac{1}{e}\approx 0.36$，也就是说 $N=\frac{1}{1-\beta }$ 天后，曲线的高度下降到了约原来的 $\frac{1}{3}$，由于时间越往前推移$\theta$ 权重越来越小，所以相当于说：我们每次只考虑最近(latest) $N=\frac{1}{1-\beta }$ 天的数据来计算当前时刻的 EMA，这也就是移动平均的来源。

1.1.3.EMA 偏差修正

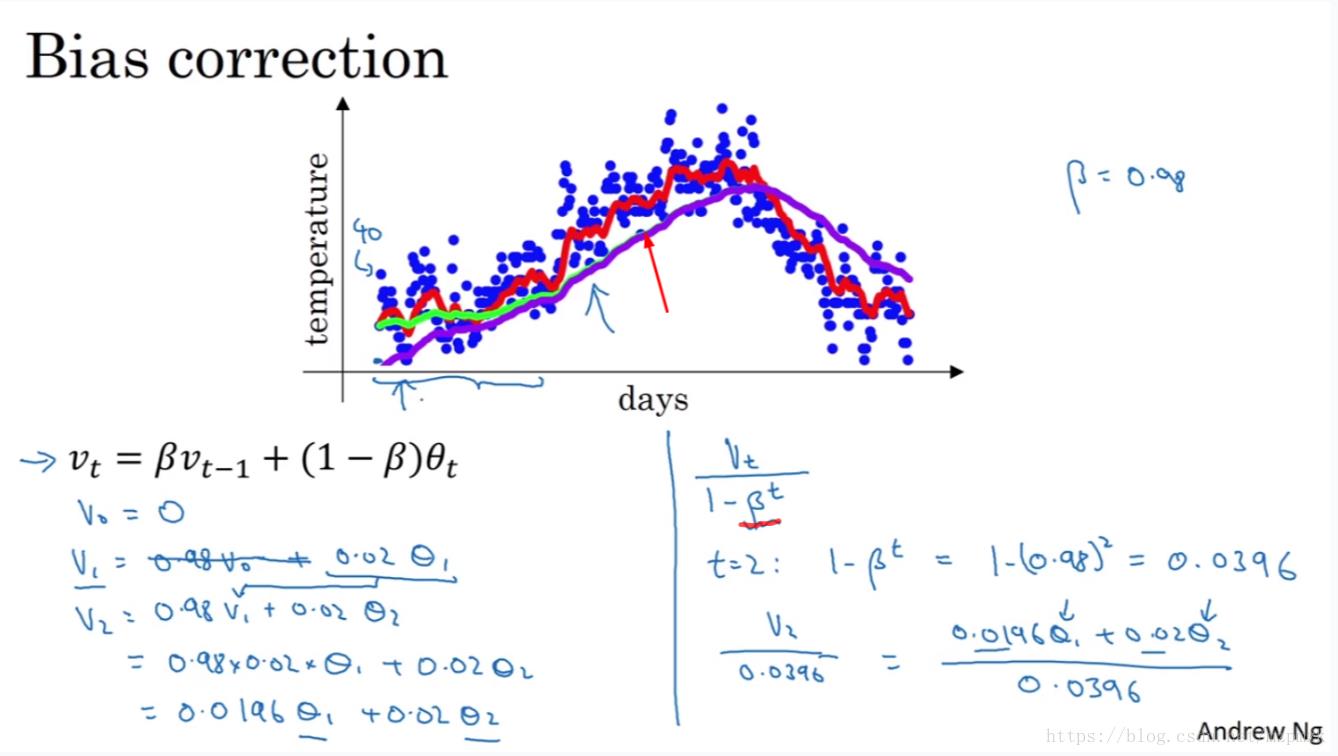
在 $\beta$ = 0.98 时，理想状况下，我们应该能得到绿色曲线，然而现实我们得到的却是紫色曲线，它的起点比真实的要低很多，不能很好的估计起始位置的温度，此问题称为：冷启动问题，这是由于 $v_0$ = 0 造成的。
解决方案：将所有时刻的 EMA 除以 $1-{\beta }^t$ 后作为修正后的 EMA。当 t 很小时，这种做法可以在起始阶段的估计更加准确；当 t 很大时，偏差修正几乎没有作用，所以对原来的式子几乎没有影响。注意：我们一般取 $\beta >=0.9$，计算 t 时刻偏修正后的 EMA 时，用的还是 t-1 时刻修正前的EMA。

1.1.4.EMA 在 Momentum 优化算法中应用的理解

假设每次梯度的值都是 g、$\gamma =0.95$ ，此时参数更新幅度会加速下降，当 n 达到 150 左右，此时达到了速度上限，之后将匀速下降（可参考一中的公式理解）。
假如，在某个时间段内一些参数的梯度方向与之前的不一致时，那么真实的参数更新幅度会变小；相反，若在某个时间段内的参数的梯度方向都一致，那么其真实的参数更新幅度会变大，起到加速收敛的作用。在迭代后期，由于随机噪声问题，经常会在收敛值附近震荡，动量法会起到减速作用，增加稳定性。

2.递归下降算法

2.1.BGD MBGD SGD

具体可参考之前的文章
或者这个参考链接：
深度学习——优化器算法Optimizer详解（BGD、SGD、MBGD、Momentum、NAG、Adagrad、Adadelta、RMSprop、Adam）

近期的的研究表明，深层神经网络之所以比较难训练，并不是因为容易进入local minimum。相反，由于网络结构非常复杂，在绝大多数情况下即使是 local minimum 也可以得到非常好的结果。而之所以难训练是因为学习过程容易陷入到马鞍面中，即在坡面上，一部分点是上升的，一部分点是下降的。而这种情况比较容易出现在平坦区域，在这种区域中，所有方向的梯度值都几乎是 0。

2.2.Momentum

动量方法旨在加速学习，特别是在面对小而连续的梯度但是含有很多噪声的时候。动量模拟了物体运动时的惯性，即在更新的时候在一定程度上会考虑之前更新的方向，同时利用当前batch的梯度微调最终的结果。这样则可以在一定程度上增加稳定性，从而更快的学习。
公式：
$$\begin{gathered} m_t=\mu \ast m_{t-1}+g_t \\ \Delta {\theta }_t=-\eta \ast m_t \end{gathered}$$

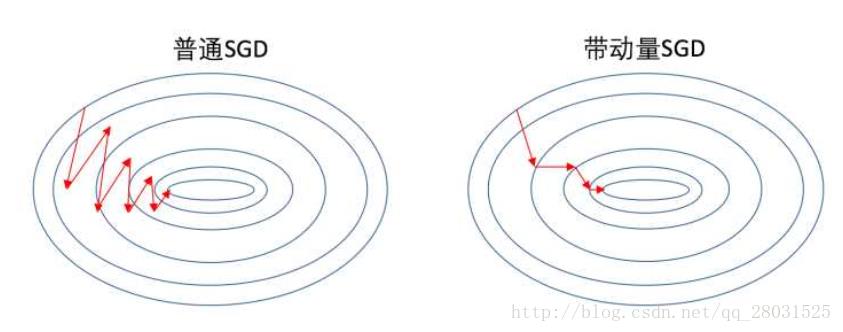
加入的这一项，可以使得梯度方向不变的维度上速度变快，梯度方向有所改变的维度上的更新速度变慢，这样就可以加快收敛并减小震荡。

超参数设定值: 一般 γ 取值 0.9 左右。

优点：

• 下降初期时，使用上一次参数更新，当下降方向一致时能够加速学习
• 下降中后期，在局部最小值附近来回振荡时，gradient–>0，使得更新幅度增大，跳出陷阱；
• 在梯度改变方向时，能减少更新。总体而言，momentum能够在相关方向上加速学习，抑制振荡，从而加速收敛

缺点：

• 这种情况相当于小球从山上滚下来时是在盲目地沿着坡滚，如果它能具备一些先知，例如快要上坡时，就知道需要减速了的话，适应性会更好。

2.3.Nesterov Accelerated Gradient

可以看到，此前积累的动量$m_{t-1}$并没有直接改变当前梯度$g_t$，所以Nesterov的改进就是让之前的动量直接影响当前的动量，即：

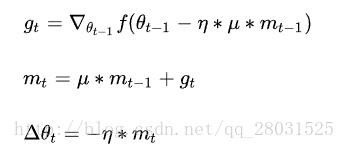
所以，加上Nesterov项后，梯度在大的跳跃后，进行计算对当前梯度进行校正。

Nesterov动量和标准动量的区别在于梯度的计算上。Nesterov动量的梯度计算是在施加当前速度之后。因此，Nesterov动量可以解释为往标准动量方法中添加了一个校正因子。
其实说白了就是当前位置在用上次的梯度先暂时更新一下$\theta$，然后再计算梯度，这样就能看到如果按照上次的梯度更新时的效果，相当于往前看了一步，这样再和之前动量结合，从而起了校正的作用

那到底为什么呢？从数学上看怎么校正的呢？看下面等效形式

这个NAG的等效形式与Momentum的区别在于，本次更新方向多加了一个$\beta [g({\theta }_{i-1})-g({\theta }_{i-2})]$，它的直观含义就很明显了：如果这次的梯度比上次的梯度变大了，那么有理由相信它会继续变大下去，那我就把预计要增大的部分提前加进来；如果相比上次变小了，也是类似的情况。这样的解释听起来好像和原本的解释一样玄，但是读者可能已经发现了，这个多加上去的项不就是在近似目标函数的二阶导嘛！所以NAG本质上是多考虑了目标函数的二阶导信息，怪不得可以加速收敛了！其实所谓“往前看”的说法，在牛顿法这样的二阶方法中也是经常提到的，比喻起来是说“往前看”，数学本质上则是利用了目标函数的二阶导信息。

其他相关参考:比Momentum更快：揭开Nesterov Accelerated Gradient的真面目

2.4 Adagrad

接下来的这几个都是自适应学习率的递归下降算法
在训练开始的时候，我们远离最终的最优值点，需要使用较大的学习率。经过几轮训练之后，我们需要减小训练学习率。
在采用mini-batch梯度下降时，迭代的过程中会伴随有噪音，虽然cost function会持续下降，但是算法收敛的结果是在最小值附近处摆动，而减小学习率，则会使得最后的值在最小值附近，更加接近收敛点。

Divide the learning rate of each parameter by the root mean square of its previous derivatives(将每个参数除以之前所有梯度的均方和)。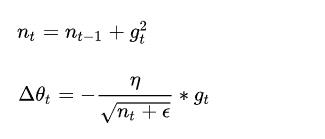
这里$n_t$是从t=1开始进行递推形成一个约束项regularizer（其实就是之前所有梯度的平方和），ε保证分母非0；

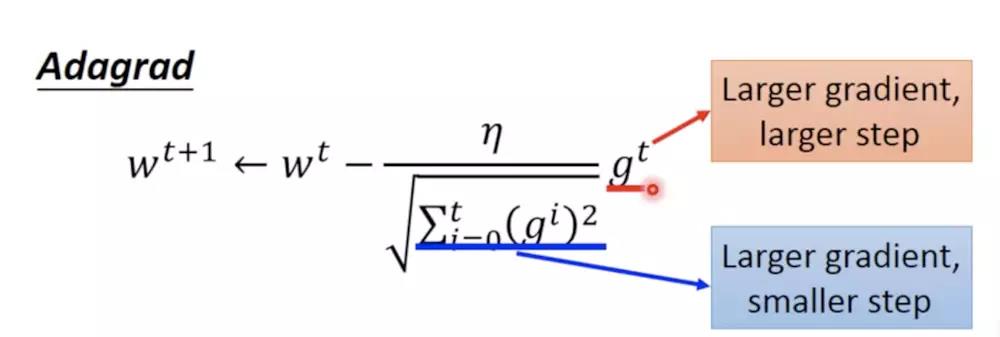
我们发现一个现象，本来应该是随着gradient的增大，我们的学习率是希望增大的，也就是图中的gt；但是与此同时随着gradient的增大，我们的分母是在逐渐增大，也就对整体学习率是减少的，这是为什么呢？
这是因为随着我们更新次数的增大，我们是希望我们的学习率越来越慢。因为我们认为在学习率的最初阶段，我们是距离损失函数最优解很远的，随着更新的次数的增多，我们认为越来越接近最优解，于是学习速率也随之变慢。

特点：
　　(1) 前期gtgt较小的时候，regularizer较大，能够放大梯度
　　(2) 后期gtgt较大的时候，regularizer较小，能够约束梯度
　　(3) 适合处理稀疏梯度。
缺点：
　　(1) 需要手动设置一个全局的学习率
　　(2) ηη设置过大时，会使regularizer过于敏感，对梯度的调节太大
　　(3) 中后期，分母上梯度平方的累积将会越来越大，使gradient–>0，使得训练提前结束

2.5.Adadelta

Adadelta是Adagrad的拓展，最初方案依旧是对学习率进行自适应约束，但是进行了计算上的简化。Adagrad会累加之前所有的梯度平方，而Adadelta只累加固定大小的项，并且也不直接存储这些项，仅仅是近似计算对应的平均值。即：

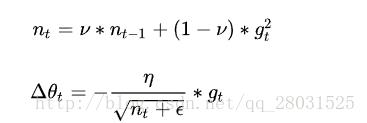
AdaDelta算法主要是为了解决AdaGrad算法中存在的缺陷，下面先介绍一下AdaGrad算法优点和以及存在的问题：

AdaGrad的迭代公式如下所示：
Δ x t = η ∑ i = 1 t g