机器学习算法笔记3. 核方法和径向基（RBF网络）

Posted 2022-12-14 tostq

【机器学习算法笔记】3. 核方法和径向基（RBF网络）

在涉及非线性可分模式分类中，多层感知器是通过神经元的非线性来达到的，这个非线性主要是通过使用Sigmoid函数来获得的。
这一节介绍另一种通过混合方式来解决非线性可分模式问题：
1、将给定非线性集合转换为线性集合
2、通过最小二乘估计来解决线性分类问题。
这个两段方法被称为核方法。

3.1 核方法

核方法的原理（模式可分性的Cover定理）：假设空间不是稠密分布的，将复杂的模式分类问题非线性地投射到高维空间将比投射到低维空间更可能是线性可分的。

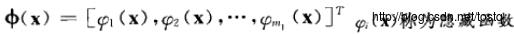
这里维数即m1，维数越高正确分类的概率也越高。
常见的核函数（径向基函数）（满足插值矩阵Φ是非奇异的）

3.2 径向基函数网络

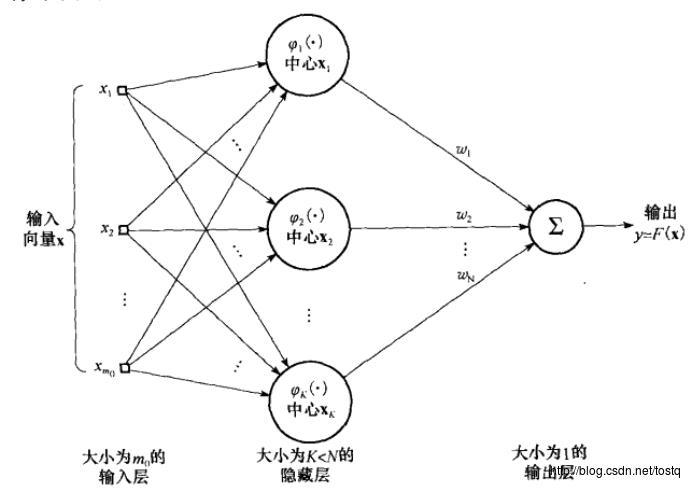
获得径向基函数中心，可以通过聚类方法来得到，如K-均值聚类：

3.2.1 K-均值聚类

K-均值聚类的代价函数：

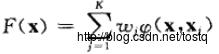
其步骤（分两步进行）
1、给定假设分类器C，计算聚类均值：

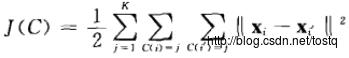
2、根据聚类均值，计算分类器：

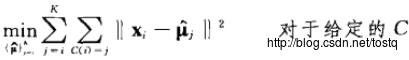
迭代上述过程，直到聚类没有变化为止

3.2.2 递归的最小二乘法（RLS）

1、r表示递归算法的输出：

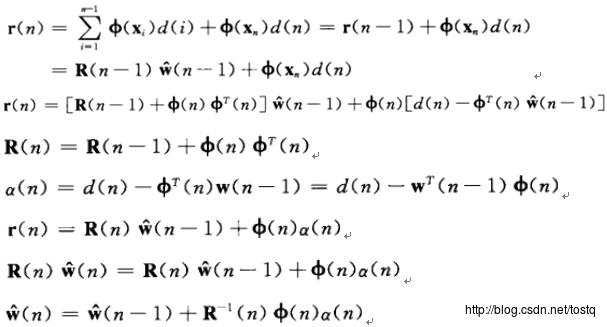
α被称为先验误差
R逆（即P(n)）的递归公式：

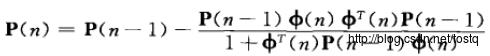
3.2.3 混合学习过程（K-均值与RLS）

1、输入层：由输入向量X的维数所决定
2、隐藏层：其大小由计划聚类数K所决定，聚类均值
3、输出层：由RLS计算权重。

3.3 多元高斯分布（GMM）

（GMM高斯混合模型）
多元高斯分布与同高斯核下RBF网络是非常相关的：
考虑一个非线性回归模型：

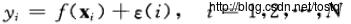
根据贝叶斯概率论：

从径向基网络上来看：

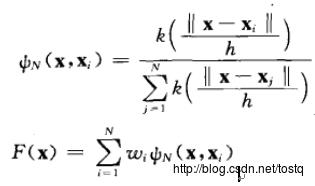
从直观上来看，对于输出f的分布，应该是各个独立分布的输入(xi)得到的独立分布输出中心（yi）,在此中心有叠加上了数个高斯分布函数，这个高斯分布的权重同输入的高斯分布权重是相关的。