静态散列

Posted 2022-12-13 xuguoli_beyondboy

散列基础知识

在静态散列方法中，把标识存储在一个固定大小的表中，使用一个函数f确定标识符x在散列表中的地址(或位置)，散列表ht存放在一片连续的内容空间中，该空间被分割为b个散列通：ht[0],….,ht[b-1],每个散列桶可以初始化s个槽，如果s=1，就意味着每个散列桶恰好可容纳一个记录。
如：
标识符的长度限定为6个字符，且第一个字符必须是字母，其余的字符可以是字母也可以是数字，那么，标识符x可能出现的不同取值共有：$\\rm T\\rm = \\sum\\limits_\\rmi = 0^\\rm5 \\rm26 \\times \\rm3\\rm6^\\rmi\\rm > 1\\rm.6 \\times \\rm1\\rm0^\\rm9.$
定义：散列表的标识符密度定义为p=n/T,散列表上的装载密度或装载因子定义为a=n/(sb)（其中n，为散列表的标识符的数量，s为一个散列桶的槽数，T为所有不同取值个数，b为散列表连续存储空间个数。）
散列算法经典两个问题：
散列函数f可能会将不同的标识符映射到相同的散列桶中，例如f($i_1$)=f($i_2$) (其中$i_1$！=$i_2$)
散列算符当把一个新的标识符i散列到一个已经满的散列桶中时，就会发生溢出。
考虑具有b=26个散列桶，每个散列桶有s=2个槽的散列表ht，现在有n=10个不同的标识符，其中每个标识符标识一个C语言的库函数，该散列表的装载因子是a=10/52=0.19,散列函数必须把所有可能出现的标识符映射为0~25中的某个整数，可以构造一个非常简单的散列函数，首先把字符a~z分别与数字0~25相对应，然后把散列函数f(x)定义为x的首字符，那么该库函数 acos，define，float，exp，char，atan，ceil，floor，clock和ctime插入散列表后如图所示：

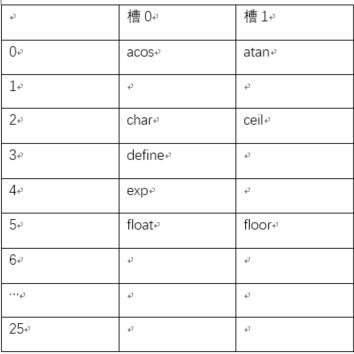
常见散列函数

• 平方取中法：构造的散列函数经常应用在符号表中，散列函数f=计算过程为：首先对标识符进行平方运算，然后从平方数的中间适当地选取若干二进制位数字作为标识符的散列桶地址，故不同的标识符产生不同散列地地址的概率非常大，但由于散列表的大小需要为2的幂次方，故需要较大存储空间，且容易造成浪费。
• 质数除余法：通过模运算可以构造另一个简单的散列函数，在该散列方式中，用标识符x除以某个数M，其余数即为x的散列地址，散列函数可以表示为：
  $f_d(x)$=x%M
  但如果M数字选取不当的话，会影响到该散列算法的效率，经过Knuth证明：M应该满足不小于20的素数因子。
• 折叠法：移位折叠法就是把除最后一个部分外的其余部分进行移位，使其最低有效位与最后一个部分的最低有效位对齐，然后把所有部分相加就得到f(x);分界折叠就是在各部分相加之前，把其中的某些部分首尾翻转。
• 数字分析法，用于静态文件中，静态文件就是指文件中的所有标识符都预先已知，数字分析法首先把所有标识符转换成某个基数r下的数，然后检查所有的标识符的数位，删除偏离分布最大的数位，重复上述删除过程，直至留下的数位个数不大于散列表地址范围。

溢出处理

1.如果新元素被散列到一个已经满的散列桶中，就必须为该元素寻找其他散列桶，最简单的处理方法是把这个新元素查到最近的未满的散列桶中，该方法称为线性探测法或线性开放定址法。
例如：如果对上面图1，把槽s改为只有1个，再通过质数除余法构造散列函数及通过线性探测法解决溢出，那么整个算法查找次数如图所示：

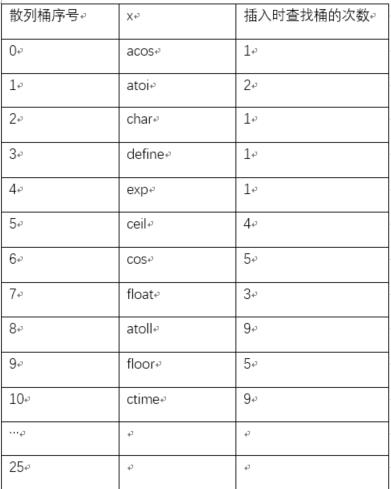
**整个算法对
每个标识符，需要检查的散列桶个数的平均值为35/11 =3.18个。**
代码实现:

#include <iostream>
#include<stdio.h>
#include<string.h>
#define MAX_CHAR 10
#define TABLE_SIZE 13
typedef struct

   char key[MAX_CHAR];
 element;
element hash_table[TABLE_SIZE];
//初始化散列表
void init_table(element ht[])

   int i;
   for(i=0;i<TABLE_SIZE;i++)
   
      ht[i].key[0]=NULL;
   

//将字符出串转换成整数
int transform(char *key)

   int number=0;
   while(*key)
      number+=*key++;
   return number;

//质数除余法
int hash(char *key)

   return (transform(key)%TABLE_SIZE);

//线性探测法解决溢出冲突
void linear_insert(element item,element ht[])

   int i,hash_value;
   //获得地址
   hash_value=hash(item.key);
   i=hash_value;
   //查找该地址是否插入了一个元素
   while(strlen(ht[i].key))
   
      //如果标识符相等
      if(!strcmp(ht[i].key,item.key))
      
         fprintf(stderr,"Duplicate entry\\n");
         return;
      
      //寻找最近的下一个为空元素的地址
      i=(i+1)%TABLE_SIZE;
      if(i==hash_value)
      
         fprintf(stderr,"the table is full\\n");
         return;
      
   
   ht[i]=item;

2.拉链散列法：函数首先计算标识符的散列地址，然后在相应的散列桶对应的单向链表中查找标识符，如果找到该标识符，则输出错误信息并退出，如果该标识符不在单向链表中，就将其插入表的尾部，如果该链表为空，修改表头结点使其指向新插入的表项。
还是拿上面图1作为例子，前面槽和构造函数与上面第一种解决溢出处理一样，那么整个算法过程如图所示：

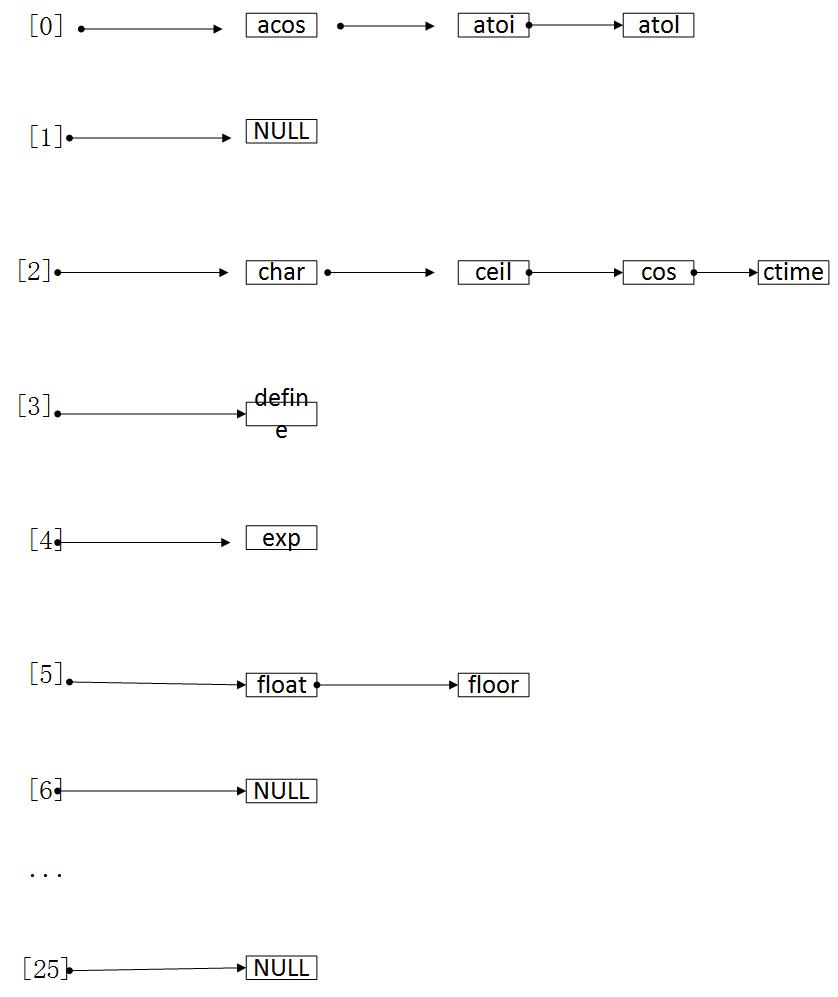
整个算法，标识符的平均比较次数为21/11=1.91
代码实现：

#include <iostream>
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define MAX_CHAR 10
#define TABLE_SIZE 13
#define IS_FULL(ptr) (!(ptr))

typedef struct

   char key[MAX_CHAR];
 element;
typedef struct list *list_pointer;
typedef struct list

   element item;
   list_pointer link;
;
list_pointer hash_table[TABLE_SIZE];
//拉链法处理溢出
void chain_insert(element item,list_pointer ht[])

   int hash_value=hash(item.key);
   list_pointer ptr,trail=NULL,lead=ht[hash_value];
   //需找该指向该桶的最后一个元素指针
   for(;lead;trail=lead,lead=lead->link)
   
      //如果标识符相等
      if(!strcmp(lead->item.key,item.key))
      
         fprintf(stderr,"Duplicate entry\\n");
         return;
      
   
   ptr=(list_pointer)malloc(sizeof(list));
   if(IS_FULL(ptr))
   
      fprintf(stderr,"the memory is full\\n");
      return;
   
   ptr->item=item;
   ptr->link=NULL;
   //插入尾部
   if(trail)
      trail->link=ptr;
   //作为该桶的第一个元素
   else
      ht[hash_value] =ptr;