蓝桥杯——要背的结论板子

Posted 2022-12-11 中二病没有蛀牙

二分查找

区间为[l, mid]和[mid + 1, r]

int bsearch_1(int l, int r)

    while (l < r)
    
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    
    return l;

区间为[l, mid - 1]和[mid , r]

int bsearch_2(int l, int r)

    while (l < r)
    
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    
    return l;

数学

常用结论

因式分解定理

$N=p_1^{a_1}\ast {p_2}^{a_2}\ast \cdot \cdot \cdot \ast p_n^{a_n}$(其中一系列$a_n$为指数，$p_n$为质数）

代码

int cnt = 0;
    for(int i = 2 ;i <= sqrt(m); i++) 
        if( n % i == 0) 
            ans.push_back(i, 0);
            while(n % i ==0)  
                n /= i;
                ans[cnt].second++;
            
            cnt++;
        
    
    if(n != 1) 
        ans.push_back(n,1);
        cnt++;
    

N的约数个数

约数个数 $（a_1+1）（a_2+1）\dots \dots （a_n+1）$

N的约数之和

约数之和$(1+{p_1}^1\ast +{p_1}^2+\cdot \cdot \cdot +{p_1}^{a_1})\ast \cdot \cdot \cdot \ast (1+{p_k}^1\ast +{p_k}^2+\cdot \cdot \cdot +{p_k}^{a_k})$

快速幂

ll ksm(ll a,ll b,ll m)
    ll res = 1;
    while(b)
        if(b & 1)
            res = res * a % m;
        a = a * a % mod;
        b >>= 1;
    
    return res;

排列组合

组合公式：$C_n^m=\frac{n!}{m!(n-m)!}$

基本性质：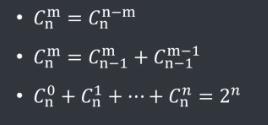

线性筛

int primes[N], cnt;
bool st[N];

void get_primes(int n)

    for (int i = 2; i <= n; i ++ )
    
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        
    

搜索

bfs

int dir[4][2] = 0,1,0,-1,1,0,-1,0;
int dx[4] = -1, 0, 1, 0, dy[4] = 0, 1, 0, -1;

struct node
    int x,y,l;
;

node s,e;
int bfs(int x,int y)

    memset(vis,-1,sizeof(vis));
    queue<node> q;
    q.push(s);
    vis[s.x][s.y] = 0;
    while(!q.empty())
        node now = q.front();
        q.pop();
        for(int i = 0; i < 4;i++)
            int nx = now.x + dx[i];
            int ny = now.y + dy[i];
            if (nx < 0 || nx >= r || ny < 0 || ny >= c) continue;  // 出界
            if (g[nx][ny] == '#') continue;  // 障碍物
            if (vis[nx][ny] != -1) continue;  // 之前已经遍历过
            node next = nx,ny,now.l+1;
            vis[nx][ny] = vis[now.x][now.y]+1;
            q.push(next);
            
        
    
    return vis[e.x][e.y];

树状数组

#include<bits/stdc++.h>
using namespace std;
const int maxn = 100010;
int s[maxn],tr[maxn];
int n,m,a,b,k;

int  lowbit(int x)
    return x & -x;


void add(int x,int v)

    for(int i = x; i <= n;i += lowbit(i))
        tr[i] +=v ;

int querry(int x)
    int  res = 0;
    for(int i = x;i ;i -= lowbit(i))
        res += tr[i];
    return res;

线段树

int s[maxn];
int n,m;

struct  node

    int l,r;
    int sum;
    /* data */
tr[maxn*4];


void pushup(int u)
    tr[u].sum = tr[u<<1].sum + tr[u << 1 | 1].sum;


void build(int u,int l,int r)
    if(l == r) tr[u] = l,r,s[r];
    else
        tr[u] = l,r;
        int mid = l +r >>1;
        build(u<<1,l,mid),build(u<<1|1,mid+1,r);
        pushup(u);
    



void modify(int u,int x,int v)

    if(tr[u].l == tr[u].r) tr[u].sum += v;
    else
        int mid= tr[u].l + tr[u].r >> 1;
        if(x <= mid) modify(u<<1,x,v);
        if(x > mid) modify(u<<1|1,x,v);
        pushup(u);
    


int querry(int u,int l,int r)
    if(tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
    int mid = tr[u].l + tr[u].r >>1;
    int sum = 0;
    if(l <= mid) sum += querry(u<<1,l,r);
    if(r > mid) sum += querry(u<<1 |1,l,r);
    return sum;

动态规划