题解：两仪剑法（nefu116）（欧几里得算法）

Posted 2022-12-11 sun897949163

两仪剑法
Problem:116

Time Limit:1000ms

Memory Limit:65536K

Description
两仪剑法是武当派武功的高级功夫，且必须2个人配合使用威力才大。同时该剑法招数变化太快、太多。设武当弟子甲招数变化周期为M，武当弟子乙招数变化周期为N，两弟子同时使用该剑法，当2人恰好同时达到招数变化周期结束时，威力最大，此时能将邪教妖人置于死地。请你计算威力最大时，每人用了多少招(用t表示）？
Input
输入数据有若干组，每组数据包含量个整数M,N（ 1< M < N < 100000 ）。
Output
对于每组数据，输出威力最大时出手了多少招（用t表示，1 < t < 1000000000）？
Sample Input
4 6
3 7
Sample Output
12
21
Hint
Source

题目分析：
经过题目分析我们可以知道这道题就是在求M,N的最小公倍数， 由最小公倍数的计算公式得

.

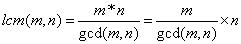
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

long long gcd(long long x, long long y)

    if(x < y)
    
        long long temp = x;
        x = y;
        y = temp;
    
    if(y == 0)
        return x;
    else
        return gcd(y, x % y);


int main (void)

    long long a, b;
    while(scanf("%lld %lld", &a, &b) != EOF)
    
        long long c = gcd(a, b);
        printf("%lld\\n", (a / c) * b);
    
    return 0;