算法模板-二分查找

Posted 2022-12-11 周先森爱吃素

简介

针对有序序列的查找问题，二分查找几乎是效率最高的算法，它的基本思路为：在指定左索引和右索引的查找空间内，维护左、右、中指示符，并比较查找目标和中间指示符对应的值的关系，如果条件不满足则清楚目标不可能在的一侧区域，在另一半区域继续查找。

解题模板

最常见的二分模板有下面三种，其中模板1和模板3是最常用的模板，几乎所有二分查找问题都可以用其中之一实现，模板2则更加高级一些，某些情况下它可能更加适用，具体可以参考LeetBook。

二分查找常见三种模板

不过，我这里的建议是，任何题目都不要死套模板，写对二分查找的重点从来不在于选择哪个模板（因为所有模板背后的逻辑都是一样的），更不在于二分查找的区间是左闭右闭还是左开右闭。而在于认真分析题意，根据题目条件和要求思考如何缩减区间，清楚地知道每一轮在什么样的情况下，搜索的范围是什么，进而设置左右边界。

下面我们具体来聊聊二分查找的算法。

二分查找的核心思想只有一个，即逐步缩小搜索区间。我们使用left和right来标定搜索区间的左右边界，并将他们向中间靠拢，这暗含的就是：当left和right重合的时候，我们就找到了问题的答案。 这种写法有一个巨大的好处，那就是返回值不需要考虑返回left和right，因为循环结束时，它们是重合的。

在解题时，会遇到两个难点：（1）取mid的时候，有的时候需要+1，这是因为需要避免死循环；（2）只把区间分为两个部分而不是三个，这是因为：只有这样，退出循环的时候才会有left和right重合，这样才能说找到了问题的答案。

题目列表

下面是力扣主站题库里典型的二分求解的题。

• leetcode-704 二分查找
• leetcode-35 搜索插入位置
• leetcode-34 在排序数组中查找元素的第一个和最后一个位置
• leetcode-74 搜索二维矩阵
• leetcode-153 寻找旋转排序数组中的最小值
• leetcode-154 寻找旋转排序数组中的最小值 II
• leetcode-33 搜索旋转排序数组
• leetcode-81 搜索旋转排序数组 II
• leetcode-875 爱吃香蕉的珂珂

题解列表

704-二分查找

原题链接

这题是二分查找最原始的问题，即在有序序列中找到目标值的位置。

我们可以使用采用两边夹得策略来查找目标，当mid位置的值严格小于目标值，那么目标值一定在mid右侧一个元素开始的闭区间内；反之，则目标值则在mid左侧的区间内（包括mid）。这种思路即使找不到目标值，最终left和right也会指向最接近的元素，因此需要后处理判断最终位置是不是问题的答案。

Python代码如下。

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
        while left < right:
            mid = (left + right) // 2
            if nums[mid] < target:
                left  = mid + 1
            else:
                right = mid
        return left if nums[left] == target else -1

35-搜索插入位置

原题链接

本题要求找到目标值的索引，如果找不到则确定其插入的位置，插入后数组依然有序。

我们不妨分析一下题意，如果target比数组最后一个元素还要大，则插在末尾（返回最后一个元素下标+1），一般情况下，若找不到target其实插入的位置就是第一个大于target的下标，综合找得到和找不到两种情况，我们其实搜索的是第一个大于等于target的元素的下标。

我们可以用left和right划分搜索区间，当mid位置的值小于target，那么第一个大于等于target的元素至少是mid右侧的元素；否则，所找元素一定在mid或者mid左侧。

Python代码如下。

class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        if target > nums[-1]: return len(nums)
        left, right = 0, len(nums) - 1
        while left < right:
            mid = (left + right) // 2
            if nums[mid] < target:
                left = mid + 1
            else:
                right = mid
        return left

34-在排序数组中查找元素的第一个和最后一个位置

原题链接

这道题要求在有序数组中找到第一个和最后一个等于target的位置。

我们可以考虑使用二分查找来寻找目标值，但是当mid位置的元素为target的时候，不能确定mid就是target第一次出现的位置，但是mid的右侧一定不是target第一次出现的位置。我们有一个思路就是看到4以后，继续向左线性查找，但是这样的复杂度为$O(N)$，实际上在左边查找可以继续二分查找。

Python代码如下。

class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
        if not nums: return [-1, -1]
        return [self.find_first(nums, target), self.find_last(nums, target)]
    
    def find_first(self, nums, target):
        left, right = 0 , len(nums) - 1
        while left < right:
            mid = (left + right) // 2
            if nums[mid] < target: left = mid + 1
            else: right = mid
        return left if nums[left] == target else -1
    
    def find_last(self, nums, target):
        left, right = 0, len(nums) - 1
        while left < right:
            mid = (left + right + 1) // 2
            if nums[mid] > target: right = mid - 1
            else: left = mid
        return left if nums[left] == target else -1

我这里简单解释一下find_first函数，当mid位置的值小于target时，mid及其左侧一定不是target第一次出现的位置，也就是说target第一次出现的位置至少在mid右侧，故有left=mid+1；当mid位置的值等于或者大于于target时（这两种情况可以合并），target第一次出现的值一定在mid位置或者其左侧，故有right=mid。

74-搜索二维矩阵

原题链接

这道题是要在一个二维矩阵中搜索目标值，矩阵有两个特性：每行中的整数从左到右按升序排列；每行的第一个整数大于前一行的最后一个整数。

这道题的有序性质很容易联想到二分查找，即我们可以先确定目标元素可能在的行然后在该行中搜索这个目标，或者我们可以干脆将二维矩阵逻辑上抽象为一维数组（通过数学计算实际行列号）用一维二分的方法来解题，这两种思路的复杂度是一致的。

第二种解法的Python代码如下。

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        m, n = len(matrix), len(matrix[0])
        left, right = 0, m * n - 1
        while left < right:
            mid = (left + right) // 2
            if matrix[mid // n][mid % n] < target:
                left = mid + 1
            else:
                right = mid
        return matrix[left // n][left % n] == target

153-寻找旋转排序数组中的最小值

原题链接

这道题是要在旋转数组中找到最小值，我们应该抽象出下图。

依据上图，我们可以很方便地将 mid和right元素进行比较并利用数组特性来确定下一步搜索的区间。具体而言，若nums[mid] > nums[right]则说明，这说明mid在最小值的左侧；若nums[mid] < nums[right]，这说明mid在最小值的右侧；由于不存在重复元素，在left和right重合之前，不会有nums[mid] == nums[right。

class Solution:
    def findMin(self, nums: List[int]) -> int:
        left, right = 0, len(nums) - 1
        while left < right:
            mid = (left + right) // 2
            if nums[mid] < nums[right]:
                right = mid
            else:
                left = mid + 1
        return nums[left]

154-寻找旋转排序数组中的最小值 II

原题链接

这道题是上一题的延申，不过难度增大了，数组中存在重复的元素，我们应该抽象出下图。

这题我们依然可以通过二分法来求解，我们通过left和right进行区间缩小，我们依然可以借助区间末端元素来处理。具体而言，当nums[mid] < nums[right]，这说明mid一定在最小值右侧，因此我们可以忽略右侧区间；当nums[mid] > nums[right]，这说明mid在最小值的左侧，因此我们可以忽略左侧区间；若nums[mid] == nums[right]，如下图，此时无法确定mid是在最小值的哪一侧，但是我们可以确定，无论nums[right]是不是最小值，区间内已经存在mid和它同样大小，因此可以忽略区间右端点。

Python代码如下。

class Solution:
    def findMin(self, nums: List[int]) -> int:
        left, right = 0, len(nums) - 1
        while left < right:
            mid = (left + right) // 2
            if nums[mid] < nums[right]:
                right = mid
            elif nums[mid] > nums[right]:
                left = mid + 1
            else:
                right -= 1
            
        return nums[left]

33-搜索旋转排序数组

原题链接

这道题要求在旋转数组中找到目标值，并返回下标，否则返回-1。

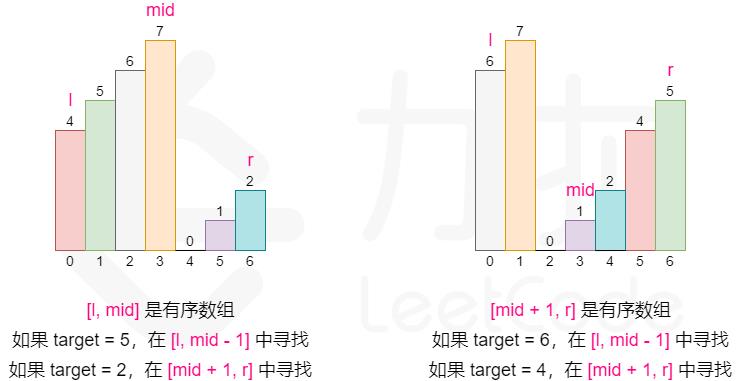
我们知道，旋转数据其实就是从数组的末端截取了一段拼接到数组的头部，因此旋转排序数组必然是两段有序数组的拼接。 因此，当我们在数组中间区域切一刀的时候（通过mid将数组分为左右两个部分），如下图，我们可以知道，[left, mid]和[mid+1, right]必有一部分是有序的，在这个有序部分中很容易判断目标值在不在该区间。

• 若[left, mid]是有序的，且target在[nums[left], nums[mid]]区间内，那么搜索范围应当缩小为[left, mid]，否则在[mid+1, right]间搜索。
• 若[mid+1, right]是有序的，且target在[nums[mid+1], nums[right]]区间内，那么搜索范围应当缩小为[mid+1, right]，否则在[left, mid]之间搜索。

对应上述思路的Python代码如下。

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
        while left < right:
            mid = (left + right) // 2
            if nums[left] <= nums[mid]:
                # [left, mid]为左半部分有序，二分判断是否在左半部分中
                if nums[left] <= target <= nums[mid]:
                    right = mid
                else:
                    left = mid + 1
            else:
                # 此时必有右半部分[mid+1, right]有序
                if nums[mid] < target <= nums[right]:
                    left = mid + 1
                else:
                    right = mid
        return left if nums[left] == target else -1

81-搜索旋转排序数组 II

原题链接

这道题是上一题的升级版，唯一的区别是此时数组中会有重复的元素。

我们可以采用和上一题类似的思路，但是会存在一种情况，那就是nums[left] == nums[mid] == nums[right]，举个例子，假设序列为[3, 1, 2, 3, 3, 3, 3]，搜索目标为target=2，我们第一次二分中点下标为3，区间[0, 3]和[4, 6]无法判断是否有序，但是我们至少知道左右边界有个替代品mid，因此可以缩小边界。

上述思路的代码可以在上一题代码基础上加个判断得到，如下。

class Solution:
    def search(self, nums: List[int], target: int) -> bool:
        left, right = 0, len(nums) - 1
        while left < right:
            mid = (left + right) // 2
            if nums[left] == nums[mid] and nums[mid] == nums[right]:
                left += 1
                right -= 1
            elif nums[left] <= nums[mid]:
                # [left, mid]为左半部分有序，二分判断是否在左半部分中
                if nums[left] <= target <= nums[mid]:
                    right = mid
                else:
                    left = mid + 1
            else:
                # 此时必有右半部分[mid+1, right]有序
                if nums[mid] < target <= nums[right]:
                    left = mid + 1
                else:
                    right = mid
        return nums[left] == target

875-爱吃香蕉的珂珂

原题链接

这道题比较复杂，我先简单复述一下，有N堆香蕉，第i堆香蕉有piles[i]根，预设一个吃香蕉的速度K，每个小时可以选择一堆香蕉吃掉其中的K个，若这堆不足K个则这个小时只能吃完这堆结束，请你给出H小时内吃完所有香蕉的最小速度K（K是一个整数）。

有时用到二分搜索的题目并不会直接给你一个有序数组，它隐含在题目中，需要你去发现或者构造。一类常见的隐含的二分搜索的问题是求某个有界数据的最值，以最小值为例，当数据比最小值大时都符合条件，比最小值小时都不符合条件，那么符合/不符合条件就构成了一种有序关系，再加上数据有界，我们就可以使用二分搜索来找数据的最小值。注意，数据的界一般也不会在题目中明确提示你，需要你自己去发现。

这题很明显是有界数据的搜索，为什么二分搜索可行呢，我们知道，如果速度K可以保证吃完，那么速度K+1，K+2也一定可以吃完，而K-1，K-2则一定不能吃完，这里存在明显的数据分界关系。二分搜索的上界显然是最多的一堆香蕉的个数（因为一次只能吃一堆），下界显然是1。现在问题就剩下，我们如何判断一个数K能否在H小时吃完呢，其实模拟这一场景，对于每一堆（有p个香蕉），需要p/K向上取整个小时才能吃完，因此只需要将每一堆的花费时间求和判断是否超过H即可（这个函数为下面代码的judge）。

Python代码如下。

class Solution:
    def minEatingSpeed(self, piles: List[int], h: int) -> int:
        def judge(k):
            # 判断能否H小时吃完
            return sum(ceil(p / k) for p in piles) <= h
        
        left, right = 1, max(piles)
        while left < right:
            mid = (left + right) // 2
            if judge(mid):
                right = mid 
            else:
                left = mid + 1
        return left

补充说明

本文参考力扣题解，以力扣上一些典型题为例进行了二分查找实际应用的介绍。