机器学习-支持向量机的SVM(Supprot Vector Machine)算法-linear inseparable
Posted YEN_csdn
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习-支持向量机的SVM(Supprot Vector Machine)算法-linear inseparable相关的知识,希望对你有一定的参考价值。
学习彭亮《深度学习基础介绍:机器学习》课程
概述
linear separable 线性可分
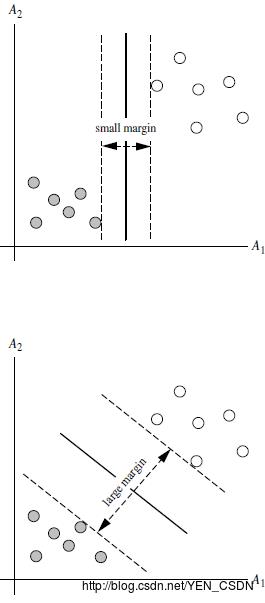
特性(优点)
- 训练好的模型的算法复杂度是由支持向量的个数决定的,若不是由数据的维度决定的。所以SVM不容易产生overfiting
- SVM训练出来的模型完全依赖于support vectors,即使训练集里面所有非支持向量的点都被去除,重复训练过程,结果依然是完全一样的模型。
- 一个SVM如果训练得到的支持向量个数比较小,SVM训练出的模型比较容易被泛华。
linear inseparable 线性不可分
linearly insepatable case:
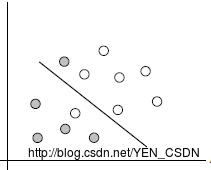
即,数据集在空间中对应的向量不可被一个超平面分开
两个步骤来解决
- 利用一个非线性的映射把原数据集中的向量点转化到一个更高维的空间中
利用这个高维空间找一个线性的超平面来根据线性可分的情况处理
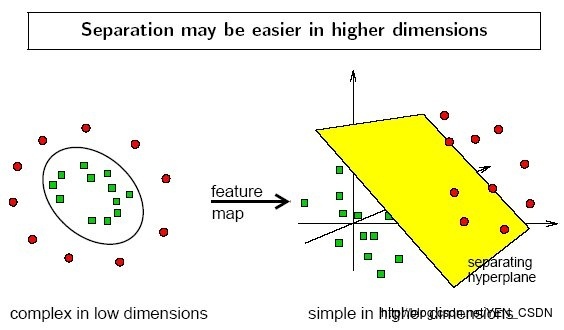
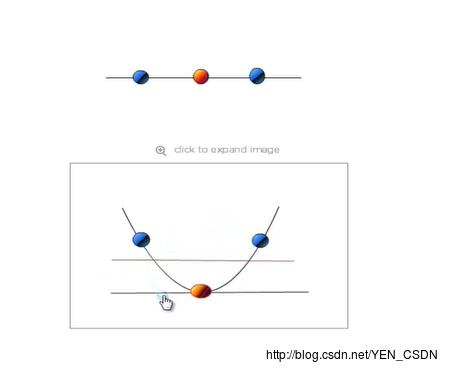
例子
3维输入向量转化为6维空间Z
3维输入向量: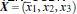
6维空间Z: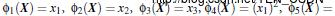
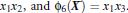
新的决策超平面:
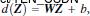
W为权重,b为偏好。其中W和Z是向量,这个超平面是线性的。
解出W和b后,并且带入回原方程:
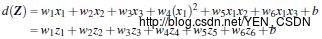
需要思考两个问题:
- 如何选择合理的非线性转化把数据转到高维中?
- 如何解决计算内积时算法复杂度非常高的问题?
使用核方法(Kernel trick)
核方法(Kernel trick)
动机
在线性SVM中转化为最优问题时求解的公式计算都是以内积(dot product)的形式出现的
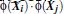
其中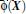
是把训练集中的向量点转化到高维的非线性映射函数,因为内积的复杂度算法非常大,所以我们利用核函数来取代计算非线性映射函数的内积。
定义函数使得该函数和非线性映射函数的内积等同
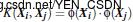
常用的核函数(Kernel functions)
- h度多项式核函数(polynomial kernel of degree h)
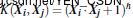
- 高斯径向基核函数(Gaussian radial basis function kernel):
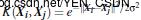
- S型核函数(Sigmoid funtion kernel):
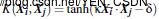 是双曲面函数
是双曲面函数
如何选择使用哪个Kernel ?
根据先验知识,比如图像分类,通过使用RBF(高斯径向基核函数),文字不使用RBF
核函数举例
假设定义两个向量:
x=(x1,x2,x3)
y=(y1,y2,y3)
定义方程:
f(x)=(x1x1,x1x2,x1x3,x2x1,x2x2,x3x3,x3x1,x3x2,x3x3)
假设
x=(1,2,3)
y=(4,5,6)
f(x)=(1,2,3,2,4,6,3,6,7)
f(y)=(16,20,24,20,25,36,24,30,36)
内积(分别相乘对应元素): < f(x),f(y) > =16+40+72+40+100+180+72+180+324=1024
定义kernel函数为:
K(x,y)=( < x,y > )^2
=(4+10+18)^2=1024
=> 同样的结果,使用kernel方法容易很多
SVM扩展和解决多个类别分类的问题
对应每个类,有一个当前类和其他类的二类分类器(one-vs-rest)
例如10个分类
=>设置10个分类器,每一类只区分他是当前类还是其他类
eg:对于第一类,只要是第一类就是1,2-10类就是0
人脸识别代码实例:
#coding=utf-8
# @Author: yangenneng
# @Time: 2018-01-12 14:52
# @Abstract:SVM-linear inseparable-人脸识别
from __future__ import print_function
from time import time
import logging
# 绘图的包
import matplotlib.pyplot as plt
from sklearn.cross_validation import train_test_split
from sklearn.datasets import fetch_lfw_people
from sklearn.grid_search import GridSearchCV
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.decomposition import RandomizedPCA
from sklearn.svm import SVC
# print(__doc__)
# 打印程序进展中的一些进展信息打印出来
logging.basicConfig(level=logging.INFO,format="%(asctime)s %(message)s")
# 数据集下载:fetch_lfw_people下载名人库Loader for the Labeled Faces in the Wild (LFW) people dataset
lfw_people = fetch_lfw_people(min_faces_per_person=70, resize=0.4)
# 返回数据集有多少个实例 h是多少 w是多少
n_samples, h, w = lfw_people.images.shape
# x矩阵用来装特征向量 得到数据集的所有实例
X = lfw_people.data
# 特征向量是多少维度的 [1]对应列数
n_features = X.shape[1]
# 每个实例对应的类别,即人的身份
y=lfw_people.target
# 返回所有的类别里人的名字
target_names=lfw_people.target_names
# 有多少类,即有多少个人要进行识别
n_classes = target_names.shape[0]
print("Total dataset size:")
print("n_samples: %d" % n_samples)
print("n_features: %d" % n_features)
print("n_classes: %d" % n_classes)
#####################拆分为训练集和测试集#############################
#X_train训练集的特征向量 X;test训练集的分类
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
#####################特征值降维度######################################
# 组成元素的数量
n_components=150
print("Extracting the top %d eigenfaces from %d faces"
% (n_components, X_train.shape[0]))
# 初始时间
t0 = time()
# 降维
pca = RandomizedPCA(n_components=n_components, whiten=True).fit(X_train)
print("done in %0.3fs" % (time() - t0))
# 提取特征量 eigenfaces从一张人脸上提取一些特征值
eigenfaces = pca.components_.reshape((n_components, h, w))
print("Projecting the input data on the eigenfaces orthonormal basis")
t0 = time()
# 把训练集特征向量转为更低维的矩阵
X_train_pca = pca.transform(X_train)
# 把训练集特征向量转为更低维的矩阵
X_test_pca = pca.transform(X_test)
print("done in %0.3fs" % (time() - t0))
#####################把降维过的特征向量结合SVM分类器进行分类######################################
print("Fitting the classifier to the training set")
t0 = time()
# 测试哪对 C和gamma 组合会产生最好的归类精确度 30中组合
# C:Penalty parameter C of the error term
# gamma:kernal function 多少的特征点被使用
param_grid = 'C': [1e3, 5e3, 1e4, 5e4, 1e5],
'gamma': [0.0001, 0.0005, 0.001, 0.005, 0.01, 0.1],
# 调用SVM进行分类 搜索哪对组合会产生最好的归类精确度 kernel:rbf高斯径向基核函数 class_weight权重
clf = GridSearchCV(SVC(kernel='rbf', class_weight='auto'), param_grid)
# 专配数据 找出边际最大的超平面
clf = clf.fit(X_train_pca, y_train)
print("done in %0.3fs" % (time() - t0))
print("Best estimator found by grid search:")
print(clf.best_estimator_)
#####################进行评估准确率计算######################################
print("Predicting people's names on the test set")
t0 = time()
# 预测新的分类
y_pred = clf.predict(X_test_pca)
print("done in %0.3fs" % (time() - t0))
# classification_report真实的分类和预测的分类进行比较
print(classification_report(y_test, y_pred, target_names=target_names))
# 建立n*n的矩阵 横行和竖行分别代表真实的标记和预测出的标记的区别 对角线上数值越多表示准确率越高
print(confusion_matrix(y_test, y_pred, labels=range(n_classes)))
#####################打印图像######################################
def plot_gallery(images, titles, h, w, n_row=3, n_col=4):
"""Helper function to plot a gallery of portraits"""
# 建立图作为背景
plt.figure(figsize=(1.8 * n_col, 2.4 * n_row))
plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35)
for i in range(n_row * n_col):
plt.subplot(n_row, n_col, i + 1)
plt.imshow(images[i].reshape((h, w)), cmap=plt.cm.gray)
plt.title(titles[i], size=12)
plt.xticks(())
plt.yticks(())
# 预测函数归类标签和实际归类标签打印
def title(y_pred, y_test, target_names, i):
pred_name = target_names[y_pred[i]].rsplit(' ', 1)[-1]
true_name = target_names[y_test[i]].rsplit(' ', 1)[-1]
return 'predicted: %s\\ntrue: %s' % (pred_name, true_name)
# 预测出的人名
prediction_titles = [title(y_pred, y_test, target_names, i)
for i in range(y_pred.shape[0])]
# 测试集的特征向量矩阵和要预测的人名打印
plot_gallery(X_test, prediction_titles, h, w)
# 打印原图和预测的信息
eigenface_titles = ["eigenface %d" % i for i in range(eigenfaces.shape[0])]
plot_gallery(eigenfaces, eigenface_titles, h, w)
plt.show()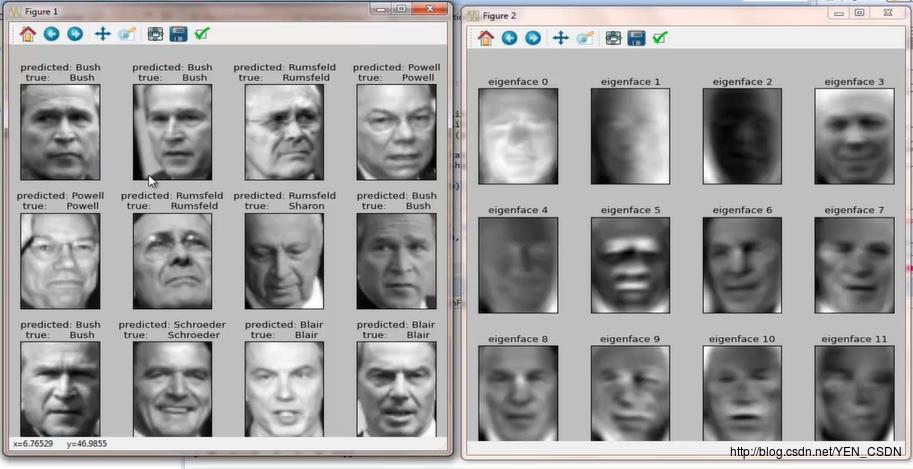
以上是关于机器学习-支持向量机的SVM(Supprot Vector Machine)算法-linear inseparable的主要内容,如果未能解决你的问题,请参考以下文章