快速浮点开方运算
Posted yutianzuijin
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了快速浮点开方运算相关的知识,希望对你有一定的参考价值。
代码下载:开根号的几种算法实现
在之前的博客中我们介绍了数据类型的地址转换,利用它我们可以将一个float型的值直接看成一个int类型。这种地址转换到底有什么意义,或者说有什么用途呢?今天,给大家展示一个实例—快速浮点开方运算,让大家更加明白地址转换的含义和它们之间的对应关系。
1 二分法
浮点开方也就是给定一个浮点数x,求 x \\sqrt x x。这个简单的问题有很多解,我们从最简单最容易想到的二分开始讲起。利用二分进行开平方的思想很简单,就是假定中值为最终解。假定下限为0,上限为x,然后求中值;然后比较中值的平方和x的大小,并根据大小修改下限或者上限;重新计算中值,开始新的循环,直到前后两次中值的距离小于给定的精度为止。**需要注意的一点是,如果x小于1,我们需要将上限置为1,原因你懂的。**代码如下:
float SqrtByBisection(float n)
float low,up,mid,last;
low=0,up=(n<1?1:n);
mid=(low+up)/2;
do
if(mid*mid>n)
up=mid;
else
low=mid;
last=mid;
mid=(up+low)/2;
while(fabsf(mid-last) > eps);
return mid;
这种方法非常直观,也是面试过程中经常会问到的问题,不过这里有一点需要特别注意:在精度判别时不能利用上下限而要利用前后两次mid值,否则可能会陷入死循环!这是因为由于精度问题,在循环过程中可能会产生mid值和up或low中的一个相同。这种情况下,后面的计算都不会再改变mid值,因而在达不到精度内时就陷入死循环。但是改为判断前后两次mid值就不会有任何问题(为啥自己想)。大家可以找一些例子试一下,这可以算是二分法中的一个trick。二分虽然简单,但是却有一个非常大的问题:收敛太慢!也即需要循环很多次才能达到精度要求。这也比较容易理解,因为往往需要迭代3到4次才能获得一位准确结果。为了能提升收敛速度,我们需要采用其它的方法。
2 牛顿迭代法
原理也比较简单,就是将中值替换为切线方程的零根作为最终解。原理可以利用下图解释(from matrix67):
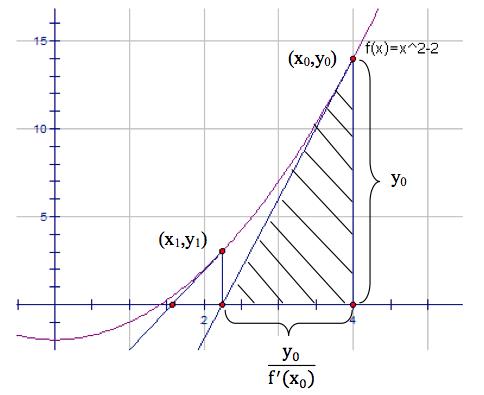
图一 牛顿迭代法求开方
假设现在要求
a
\\small \\sqrta
a的值(图中a=2),我们将其等价转化为求函数
y
=
x
2
−
a
\\small \\small y=x^2-a
y=x2−a与x轴大于0的交点。为了获得该交点的值,我们先假设一个初始值,在图一中为
x
0
=
4
\\small \\small x_0=4
x0=4。过
x
=
x
0
\\small \\small x=x_0
x=x0的直线与
y
=
x
2
−
2
\\small \\small y=x^2-2
y=x2−2交于一点
(
x
0
,
y
0
)
\\small \\small \\left ( x_0,y_0 \\right )
(x0,y0),过该点做切线交x轴于
x
1
\\small \\small x_1
x1,则
x
1
\\small \\small x_1
x1是比
x
0
\\small x_0
x0好的一个结果。重复上述步骤,过
x
=
x
1
\\small \\small x=x_1
x=x1直线与
y
=
x
2
−
2
\\small \\small y=x^2-2
y=x2−2交于一点
(
x
1
,
y
1
)
\\small \\small \\left (x_1,y_1 \\right )
(x1,y1),过该点做切线交x轴于
x
2
\\small \\small x_2
x2,则
x
2
\\small \\small x_2
x2是比
x
1
\\small \\small x_1
x1更好的一个结果……
很明显可以看出该方法斜着逼近目标值,收敛速度应该快于二分法。但是如何由
x
0
\\small x_0
x0获得
x
1
\\small \\small x_1
x1呢,我们需要获得一个递推公式。看图中的阴影三角形,竖边的长度为
y
0
\\small \\small y_0
y0,如果我们能求得横边的长度l,则很容易得到
x
1
=
x
0
−
l
\\small \\small x_1=x_0-l
x1=x0−l。因为三角形的斜边其实是过
(
x
0
,
y
0
)
\\small \\small \\left ( x_0,y_0 \\right )
(x0,y0)的切线,所以我们可以很容易知道该切线的斜率为
f
′
(
x
0
)
\\small \\small f'(x_0)
f′(x0),然后利用正切的定义就可以获得l的长度为
y
0
f
′
(
x
0
)
\\small \\small \\fracy_0f'(x_0)
f′(x0)y0,由此我们得到递推公式为:
x
i
=
x
i
−
1
−
y
0
f
′
(
x
0
)
=
x
i
−
1
−
x
i
−
1
2
−
a
2
∗
x
i
−
1
=
1
2
(
x
i
−
1
+
a
x
i
−
1
)
\\small \\small x_i=x_i-1-\\fracy_0f'(x_0)=x_i-1-\\fracx_i-1^2-a2*x_i-1=\\frac12\\left ( x_i-1+\\fracax_i-1 \\right )
xi=xi−1−f′(x0)y0=xi−1−2∗xi−1xi−12−a=21(xi−1+xi−1a)
后面我们需要做的就是利用上面的公式去迭代,直到达到精度要求,代码如下:
float SqrtByNewton(float x)
float val=x;//初始值
float last;
do
last = val;
val =(val + x/val) / 2;
while(fabsf(val-last) > eps);
return val;
对上述代码进行测试,结果确实比二分法快,对前300万的所有整数进行开方的时间分别为1600毫秒和1000毫秒,快的原因主要是迭代次数比二分法更少。虽然牛顿迭代更快,但是还有进一步优化的余地:首先牛顿迭代的代码中有两次除法,而二分法中只有一次,通常除法要比乘法慢个几倍,因而会导致单次迭代速度的下降,如果能消除除法,速度还能提高不少,后面会介绍没有除法的算法;其次我们选择原始值作为初始估值,这其实不是一个好的估计,这就导致需要迭代多次才能达到精度要求。当然二分法也存在这个问题,但是上下限不容易估计,只能采用最保守的方式。而牛顿迭代则可以任意选择初始值,所以就存在选择的问题。
我们分析一下为什么牛顿迭代法可以任意选择初值(当然必须要大于0)。由公式
x
i
=
1
2
(
x
i
−
1
+
a
x
i
−
1
)
\\small \\small x_i=\\frac12\\left ( x_i-1+\\fracax_i-1 \\right )
xi=21以上是关于快速浮点开方运算的主要内容,如果未能解决你的问题,请参考以下文章