最长公共子序列（LCS）和逆LCS问题求解

Posted 2022-12-09 地球太危险了

目录

一、子序列定义

二、公共子序列定义

三、最长公共子序列（LCS）

1、最优子结构

2、构造递归表达式

3、计算最优值

四、逆LCS问题

1、题目

2、最优子结构

3、构造递归表达式

4、计算最优值

---

一、子序列定义

一个给定序列的子序列是在该序列中删去若干元素后得到的序列。

数学定义为：给定序列X = x1, x2, ..., xm，另一序列为Z = z1, z2, ..., zk是X的子序列是指存在一个严格递增的下标序列i1, i2, ..., ik使得对于所有j = 1, 2, ..., k有：zj = xij。例如：序列Z = B, C, D, B是序列X = A, B, C, B, D, A, B的子序列。

二、公共子序列定义

给定两个字符序列，其两者的公共子序列是说这个公共子序列都是这两个字符序列的子序列。

三、最长公共子序列（LCS）

1、最优子结构

最长公共子序列的结构有如下表示：

    设序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的一个最长公共子序列Z=<z1, z2, …, zk>，则：

1. 若xm=yn，则zk=xm=yn且Zk-1是Xm-1和Yn-1的最长公共子序列；
2. 若xm≠yn且zk≠xm ，则Z是Xm-1和Y的最长公共子序列；
3. 若xm≠yn且zk≠yn ，则Z是X和Yn-1的最长公共子序列。

其中Xm-1=<x1, x2, …, xm-1>，Yn-1=<y1, y2, …, yn-1>，Zk-1=<z1, z2, …, zk-1>。

2、构造递归表达式

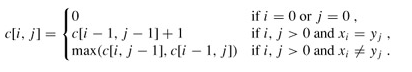
3、计算最优值

#include <iostream>
#include <string.h>
using namespace std;
const int maxn = 50;
char a[maxn], b[maxn];
int dp[maxn][maxn];
int main ()
	dp[0][0] = 0;
	scanf("%s%s" , a+1, b+1);
	int len1 = strlen(a+1);
	int len2 = strlen(b+1);
	int i, j;
	for(i = 1; i <= len1; i++) dp[i][0] = 0;
	for(j = 1; j <= len2; j++) dp[0][j] = 0;
	for(i = 1; i <= len1; i++)
		for(j = 1; j <= len2; j++)
			if(a[i] == b[j]) dp[i][j] = dp[i-1][j-1] + 1;
			else if(dp[i-1][j] >= dp[i][j-1]) dp[i][j] = dp[i-1][j];
			else dp[i][j] = dp[i][j-1];
		
	cout<<dp[len1][len2]<<endl;
	
	return 0;
 

四、逆LCS问题

1、题目

给定两个字符串s1，s2，如何求一个最短的字符串，使得s1，s2是这个字符串的子序列。并给出有几个这样的最短字符串（因为可能不止一个）。

2、最优子结构

最长公共子序列的结构有如下表示：

    设序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的一个最短逆序列Z=<z1, z2, …, zk>，则：

1. 若xm=yn，则zk=xm=yn且Zk-1是Xm-1和Yn-1的最短逆序列；
2. 若xm≠yn且zk=xm ，则Zk-1是Xm-1和Y的最短逆序列；
3. 若xm≠yn且zk=yn ，则Zk-1是X和Yn-1的最短逆序列；

其中Xm-1=<x1, x2, …, xm-1>，Yn-1=<y1, y2, …, yn-1>，Zk-1=<z1, z2, …, zk-1>。

3、构造递归表达式

4、计算最优值

#include <iostream>
#include <string.h>
#define ll long long
using namespace std;
const int maxn = 50;
ll dp[maxn][maxn], num[maxn][maxn]; // dp为长度，num为此长度的最小逆序列数量 
char a[maxn], b[maxn];
int main ()
	dp[0][0] = 0;
	num[0][0] = 1;
	scanf("%s%s", a+1, b+1);
	int len1 = strlen(a+1);
	int len2 = strlen(b+1);
	int i, j;
	for(i = 1; i <= len1; i++) dp[i][0] = i, num[i][0] = 1;
	for(j = 1; j <= len2; j++) dp[0][j] = j, num[0][j] = 1;
	for(i = 1; i <= len1; i++)
		for(j = 1; j <= len2; j++)
			if(a[i] == b[j])
				dp[i][j] = dp[i-1][j-1] + 1;
				num[i][j] = num[i-1][j-1];
			else
				if(dp[i-1][j] > dp[i][j-1])
					dp[i][j] = dp[i][j-1] + 1;
					num[i][j] = num[i][j-1];
				
				else if(dp[i-1][j] < dp[i][j-1])
					dp[i][j] = dp[i-1][j] + 1;
					num[i][j] = num[i-1][j];
				
				else //  两种情况下长度相等，所以总的数量等于两者之和 
					dp[i][j] = dp[i-1][j] + 1;
					num[i][j] = num[i-1][j] + num[i][j-1];
				
			
		
	cout<<dp[len1][len2]<<" "<<num[len1][len2]<<endl; 
	return 0;