3d变换基础:平移旋转缩放(仿射变换)详解——公式推导
Posted tiny_ten
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了3d变换基础:平移旋转缩放(仿射变换)详解——公式推导相关的知识,希望对你有一定的参考价值。
文章目录
是时候整理一波3d变换相关的知识了。模型的变换可以认为是空间中一堆点的变换,三维空间中,(x,y,z)可以认为是点,也可以认为是一个向量,因此,人们引入的第4个维度来标识是点还是向量,这个4维空间就叫 仿射空间,具体可以参考 CV及CG数学基础:空间,在仿射空间中,(x,y,z,0)标识向量,而(x,y,z,1)表示点。
平移、旋转、缩放
平移
平移没什么好说的,(x,y,z,1)向x,y,z轴分别移动a,b,c单位长度后变成(x+a, y+b, z+c, 1)。写成矩阵相乘的方式即为:
[ x + a y + b z + c 1 ] = [ 1 0 0 a 0 1 0 b 0 0 1 c 0 0 0 1 ] [ x y z 1 ] \\left[ \\beginmatrix x+a \\\\ y+b \\\\ z+c \\\\ 1\\\\ \\endmatrix \\right] = \\left[ \\beginmatrix 1 & 0 & 0 & a\\\\ 0 & 1 & 0 & b \\\\ 0 & 0 & 1 & c \\\\ 0 & 0 & 0 & 1 \\endmatrix \\right] \\left[ \\beginmatrix x \\\\ y \\\\ z \\\\ 1\\\\ \\endmatrix \\right] ⎣⎢⎢⎡x+ay+bz+c1⎦⎥⎥⎤=⎣⎢⎢⎡100001000010abc1⎦⎥⎥⎤⎣⎢⎢⎡xyz1⎦⎥⎥⎤
旋转
对于旋转,任何一个旋转都可以认为是沿着x,y,z轴分别旋转 α \\alpha α, β \\beta β, γ \\gamma γ 度数,所以选旋转就先讲沿着某个轴向的旋转。这里以逆着坐标轴正向方向看去的顺时针为旋转的正向,就是你的视线朝向和坐标轴正向是相反的,(⊙o⊙)…我还是画个图吧,下图就是沿着z轴旋转的正向了哈~
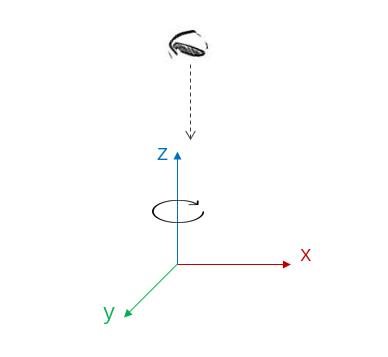
1. 沿x轴旋转
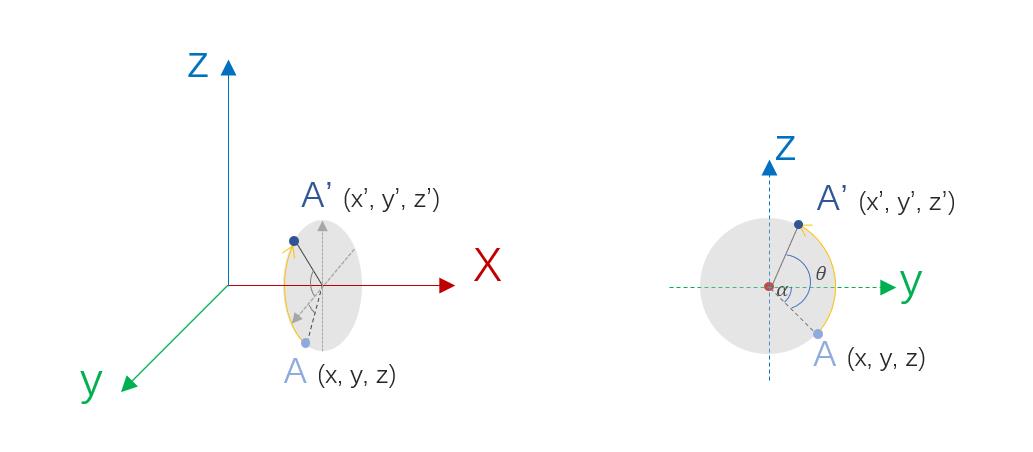
嗯!这里推一波公式,其实很简单,就是三角函数。
如上图左边,A点沿着x轴旋转一定角度变成A’,为了更容易看,右图是左图的左视图,记旋转的角度为
θ
\\theta
θ, 旋转后得到的A’与旋转中心连线与y轴正方向的夹角为
α
\\alpha
α(图中的
α
\\alpha
α是个负值),记A’与旋转中心连线的长度为L(A与旋转中心连线的长度也是L),那么,显而易见,有:
x ′ = x y ′ = L ⋅ c o s ( θ + α ) z ′ = L ⋅ s i n ( θ + α ) \\beginaligned x' =& x\\\\ y' =& L·cos(\\theta + \\alpha)\\\\ z' =& L·sin(\\theta + \\alpha) \\endaligned x′=y′=z′=xL⋅cos(θ+α)L⋅sin(θ+α)
y
=
L
⋅
c
o
s
α
z
=
L
⋅
s
i
n
α
\\beginaligned y =& L·cos\\alpha\\\\ z =& L·sin\\alpha \\endaligned
y=z=L⋅cosαL⋅sinα
根据三角函数公式可以得到
y
′
=
L
⋅
c
o
s
(
α
−
θ
)
=
L
⋅
(
c
o
s
α
c
o
s
θ
−
s
i
n
α
s
i
n
θ
)
=
y
c
o
s
θ
−
z
s
i
n
θ
z
′
=
L
⋅
s
i
n
(
α
−
θ
)
=
L
⋅
(
s
i
n
θ
c
o
s
α
+
c
o
s
θ
s
i
n
α
)
=
y
s
i
n
θ
+
z
c
o
s
θ
\\beginaligned y' =& L·cos(\\alpha - \\theta) = L·(cos\\alpha cos\\theta - sin\\alpha sin\\theta) = ycos\\theta -zsin\\theta\\\\ z' =& L·sin(\\alpha - \\theta) = L·(sin\\theta cos\\alpha + cos\\theta sin\\alpha ) = ysin\\theta + zcos\\theta \\endaligned
y′=z′=L⋅cos(α−θ)=L⋅(cosαcosθ−sinαsinθ)=ycosθ−zsinθL⋅sin(α−θ)=L⋅(sinθcosα+cosθsinα)=ysinθ+zcosθ
综上,有:
x
′
=
x
y
′
=
y
c
o
s
θ
−
z
s
i
n
θ
z
′
=
y
s
i
n
θ
+
z
c
o
s
θ
\\beginaligned x' =& x\\\\ y' =& ycos\\theta -zsin\\theta\\\\ z' =&ysin\\theta + zcos\\theta \\endaligned
x′=y′=z′=xycosθ−zsinθysinθ+zcosθ
现在就可以写成漂亮的矩阵形式了:
[
x
′
y
′
z
′
1
]
=
[
1
0
0
0
0
c
o
s
θ
−
s
i
n
θ
0
0
s
i
n
θ
c
o
s
θ
0
0
0
0
1
]
[
x
y
z
1
]
\\left[ \\beginmatrix x' \\\\ y' \\\\ z' \\\\ 1\\\\ \\endmatrix \\right] = \\left[ \\beginmatrix 1 & 0 & 0 & 0\\\\ 0 & cos\\theta & -sin\\theta & 0 \\\\ 0 & sin\\theta & cos\\theta & 0 \\\\ 0 & 0 & 0 & 1 \\endmatrix \\right] \\left[ \\beginmatrix x \\\\ y \\\\ z \\\\ 1\\\\ \\endmatrix \\right]
⎣⎢⎢⎡x′y′z′1⎦⎥⎥⎤=⎣⎢⎢⎡10000cosθsinθ00−sinθcosθ0以上是关于3d变换基础:平移旋转缩放(仿射变换)详解——公式推导的主要内容,如果未能解决你的问题,请参考以下文章