最长上升子序列模型
Posted Debroon
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最长上升子序列模型相关的知识,希望对你有一定的参考价值。
最长上升子序列模型
前置知识:最长上升子序列。
AcWing 1017. 怪盗基德的滑翔翼

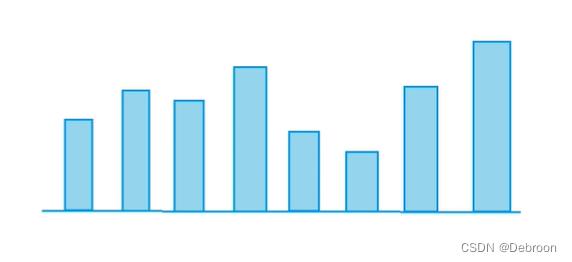
最优解,是某个起点的最长下降子序列。
- 最长下降子序列的状态是一维的
dp[n] - 起点是一个变量,需要每个顶点都试一次
- 这个题目的最长下降子序列,不止可以从左边走,还可以从右边走,所以俩边都需要做一次
int res = 0;
for (int i = 0; i < n; i ++ ) // 向右边遍历,枚举所有顶点作为起始点
f[i] = 1; // 最简单的情况,长度是自己
for (int j = 0; j < i; j ++ ) // 考虑 f[i] 前面的数,可不可以
if ( h[i] < h[j] ) // 保证是下降的
f[i] = max(f[i], f[j] + 1); // f[i] 从哪里来?自身 或 前面的 + 1
res = max(res, f[i]); // 向右走的最长下降子序列
memset(f, 0, sizeof f);
for (int i = n - 1; i >= 0; i -- ) // 向左边遍历,原理同上
f[i] = 1;
for (int j = n - 1; j > i; j -- )
if ( h[i] < h[j])
f[i] = max(f[i], f[j] + 1);
res = max(res, f[i]);
AcWing 1014. 登山

登山的限制:
- 上山,只能向上爬
- 下山,只能向下走
- 走过尽可能多的景点

问题就变成了:最长上升子序列 + 最长下降子序列
- 细节:需要 - 1,因为最长上升子序列的终点和最长下降子序列的起点重合了
for (int i = 0; i < n; i ++ )
f[i] = 1;
for (int j = 0; j < i; j ++ )
if (h[i] > h[j])
f[i] = max(f[i], f[j] + 1);
for (int i = n - 1; i >= 0; i -- )
g[i] = 1;
for (int j = n - 1; j > i; j -- )
if (h[i] > h[j])
g[i] = max(g[i], g[j] + 1);
int res = 0;
for (int i = 0; i < n; i ++ ) res = max(res, f[i] + g[i] - 1);
return res;
AcWing 482. 合唱队形

合唱队形 = 上升子序列 + 下降子序列 - 1

这题目看了几遍没看懂。
- 就是卡在,最少需要几位同学出列,才能让剩下的同学排成合唱队形。
最少出列,意味着让合唱队形最长。
- 问题是:合唱队形最长是多少?
最长合唱队形 = 最长上升子序列 + 最长下降子序列 - 1
代码和上一题没有区别。
- 上一题,返回 res
- 这一题,返回 n - res
AcWing 1012. 友好城市

题目:建最多的航线
- 俩岸的友好城市才能建一条
- 航线不能交叉
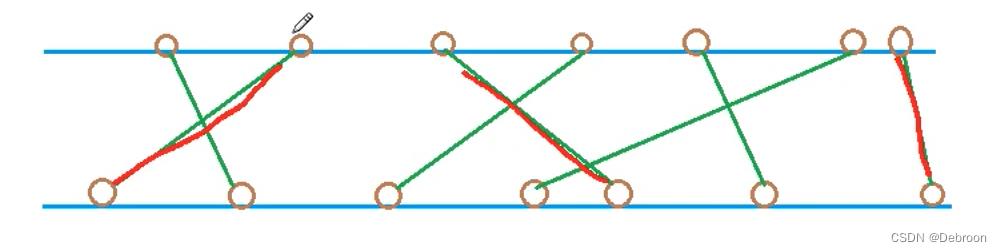
最关键的抓手是,不能相交是啥意思呢?
- 把不能相交,转化为上升子序列
- 把最多不相交,转化为最长上升子序列
我们按照自变量顺序排序,不相交序列如下:
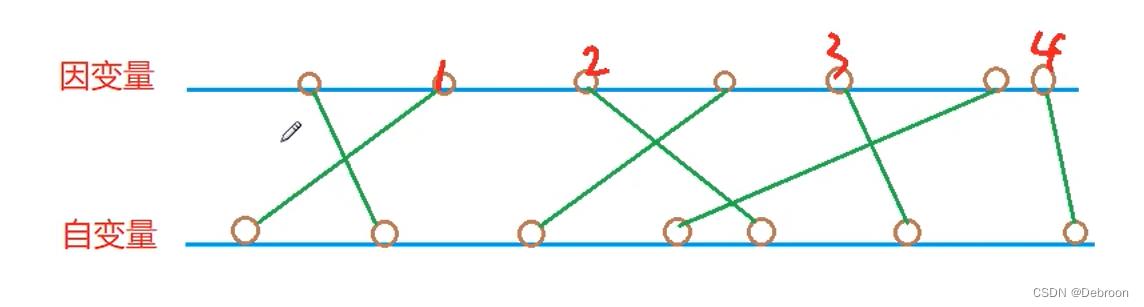
相交序列如下:

我们将一边的城市坐标从小到大排序,可以发现令航线不交错的方法即,为找到另一边的城市坐标的最长上升子序列。
#include <iostream>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 5010;
int n;
PII city[N];
int f[N];
int main()
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d %d", &city[i].first, &city[i].second);
sort(city, city + n);
int res = 0;
for (int i = 0; i < n; i ++ )
f[i] = 1;
for (int j = 0; j < i; j ++ )
if (city[i].second > city[j].second)
f[i] = max(f[i], f[j] + 1);
res = max(res, f[i]);
printf("%d\\n", res);
return 0;
AcWing 1016. 最大上升子序列和

最长上升子序列的和,从哪里来?
- 最简单的情况:f[0] = w[0],等于自身权重
- f[n] 从哪里来:max(f[n], f[前面的某数]+w[n])
逻辑和最长子序列,没什么不同,只是改一下初始值、权重。
- 但和最长上升子序列不同的是,最长上升子序列的和最终结果不是 f[n] 最大
比如序列(100,1,2,3)的最大上升子序列和为100,而最长上升子序列为(1,2,3)。
所以,我们在每轮循环后,还需要选出当前轮的最大值和下一轮最大值比较。
一组擂台,只能选出一组的最大值。
N组擂台,需要把每组的最大值再来打一次,才能选出最终的最大值。
int res = 0;
for (int i = 0; i < n; i ++ )
f[i] = w[i];
for (int j = 0; j < i; j ++ )
if (w[i] > w[j])
f[i] = max(f[i], f[j] + w[i]);
res = max(res, f[i]); // 最终的最大值擂台
AcWing 1010. 拦截导弹

这题比较特别:
- 第一问:这套系统最多能拦截多少导弹,就是求一个最长上升子序列。
- 第二问:拦截所有导弹最少要配备多少套系统,就是用最少的最长上升子序列覆盖。
我们用贪心思路想,就是每个子序列越大越好,每个都是最长上升子序列,就会最少。
- 当然贪心策略是很简单的,主要是证明难。
- 局部最优解是否等于全局最优解呢?
- 等于,具体证明我也不会,省略。
- 数学好的大佬,可以来写下。
贪心流程,从前往后扫描每个数,对于每个数:
- 情况1:如果现有的子序列的结尾都小于当前数,则只能创建新的子序列,子序列数量+1。
- 情况2:将当前数放到结尾大于等于它的最小的子序列后面,组成子序列长度+1。
举个例子,现在选择了 389,形成系统 1,后面的 207 有俩种选择:

发现了吗?这个思想不就是贪心接最长的上升子序列吗?
第二问的贪心做法:

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010, INF = 30010;
int n, x;
int w[N], f[N];
int q[N], cnt;
int main()
while (cin >> x) w[ ++ n] = x;
//对于第一问,先做一遍最长上升子序列模型DP
int res = 0;
w[0] = INF;
for (int i = 1; i <= n; ++ i)
for (int j = 0; j < i; ++ j)
if (w[j] >= w[i]) f[i] = max(f[i], f[j] + 1);
res = max(res, f[i]);
cout << res << endl;
//对于第二问,我们采用题解中所说的贪心思路
for (int i = 1; i <= n; ++ i)
int l = 0, r = cnt; //二分出插入的区间左端点
while (l < r)
int mid = l + r >> 1;
if (q[mid] >= w[i]) r = mid; //右边的性质满足q[k] >= w[i]
else l = mid + 1;
if (q[r] < w[i]) r ++ ; //处理边界,当没有能够满足当前高度的系统时,再开一个
cnt = max(cnt, r);
q[r] = w[i];
cout << cnt << endl;
return 0;
AcWing 187. 导弹防御系统
AcWing 272. 最长公共上升子序列
以上是关于最长上升子序列模型的主要内容,如果未能解决你的问题,请参考以下文章