神经网络--记一次西瓜书阅读
Posted 想考北航的小刺猬
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了神经网络--记一次西瓜书阅读相关的知识,希望对你有一定的参考价值。
神经网络–记一次西瓜书阅读
bgm:《留香》---- 许嵩
神经元模型:
M-P神经元模型:神经元接收n个来自其他神经元传递过来的输入信号,这些输入信号通过带权重的连接进行传递,神经元接收到的总输入值与神经元阈值进行比较,通过激活函数处理产生神经元的输出.
常见的激活函数:
- 阶跃函数: f ( x ) = 1 , x >= 0 0 , x < 0 f(x) = \\begincases 1, & \\text x >= 0 \\\\ 0, & \\textx < 0 \\endcases f(x)=1,0,x >= 0 x < 0
- sigmoid函数: s i g m o i d ( x ) = 1 1 + e − x sigmoid(x) = \\frac11 + e^-x sigmoid(x)=1+e−x1
感知机与多层网络
-
感知机:由两层神经元组成,输入层接收外界输入信号,传递给输出层,输出层是M-P神经元(阈值逻辑单元),感知机能容易的实现逻辑运算(使用阶跃函数作为激活函数),一般处理线性可分的问题,也就是可以用一个线性超平面分割的问题。
-
对于非线性问题,使用多层功能神经元,输入层与输出层之间的一层神经元被称为隐层或者隐含层,隐含层和输出层的的神经元都是拥有激活函数的功能神经元。每层神经元只与下一层神经元相连,神经元之间不存在同层相连,也不存在跨层相连,这样的神经网络被称为多层前馈神经网络。
-
神经网络学习过程中,根据训练数据来调整神经元之间的“连接权”以及每个功能神经元的阈值,神经网络学到的东西蕴藏在连接权和阈值当中。
误差逆传播算法
误差逆传播(error BackPropagation,简称BP),用于训练多层神经网络。BP算法不仅可以用于多层前馈神经网络,也可以用于其他类型的神经网络。BP网络一般指用BP算法训练多层前馈神经网络。
如图,BP网络(图片来源于《机器学习》–周志华)
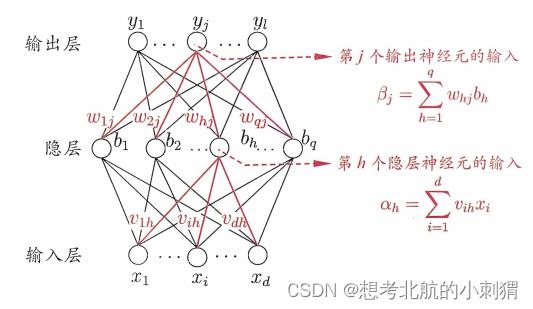
网络中需要确定的参数:
(
d
+
1
+
l
)
×
q
+
l
(d + 1 + l)\\times q + l
(d+1+l)×q+l
个人理解为:
- 输出层到隐层的边(连接权): d × q d \\times q d×q
- 隐层的神经元输出: q q q
- 隐层到输出层的边(连接权): l × q l \\times q l×q
- 输出层神经元输出: l l l
参数变化量的计算:
对某一样本
(
x
k
,
y
k
)
(x_k, y_k)
(xk,yk),假定神经网络输出为
y
^
=
(
y
1
k
^
,
y
2
k
^
,
.
.
.
,
y
l
k
^
)
\\haty = (\\haty_1^k, \\haty_2^k, ..., \\haty^k_l)
y^=(y1k^,y2k^,...,ylk^)
其中
y
j
k
^
=
f
(
β
j
−
θ
j
)
\\haty_j^k = f(\\beta_j-\\theta_j)
yjk^=f(βj−θj),这里面
β
j
=
∑
h
=
1
q
w
h
j
b
h
\\beta_j = \\sum_h = 1^qw_hjb_h
βj=∑h=1qwhjbh(
b
h
b_h
bh表示隐层的第
h
h
h个功能神经元,
θ
j
\\theta_j
θj表示输出层的阈值)
在样本上的均方误差(针对样本
k
k
k来说,样本
k
k
k的均方误差):
E
k
=
1
2
∑
j
=
1
l
(
y
j
k
^
−
y
j
k
)
2
E_k = \\frac12\\sum_j = 1^l(\\haty_j^k - y_j^k)^2
Ek=21∑j=1l(yjk^−yjk)2
对于任意参数 v v v更新的估计式为: v ← v + Δ v v \\leftarrow v + \\Delta v v←v+Δv
也就是说任意参数的更新需要基于上述的公式,这里的 Δ v \\Delta v Δv的计算根据梯度下降策略, Δ v = − η ∂ E ∂ v \\Delta v = -\\eta\\frac\\partial E \\partial v Δv=−η∂v∂E
书中给出的为
Δ
w
h
j
=
−
η
∂
E
k
∂
w
h
j
\\Delta w_hj = -\\eta\\frac\\partial E_k\\partial w_hj
Δwhj=−η∂whj∂Ek
这里面的
w
h
j
w_hj
whj表示,从隐层中第
h
h
h个(例子中一共
q
q
q个)神经元到输出层中第
j
j
j个(例子中一个
l
l
l个)神经元的连接权。
可以知道,神经网络通过梯度下降对参数进行调整,梯度下降的目标函数也就是均方误差,对这个目标函数求梯度,也就是在各个方向上求偏导。
∂
E
k
∂
w
h
j
=
∂
E
k
∂
y
j
k
^
⋅
∂
y
j
k
^
∂
β
j
⋅
∂
β
j
∂
w
h
j
\\frac\\partial E_k\\partial w_hj = \\frac\\partial E_k\\partial \\haty_j^k\\cdot \\frac\\partial \\haty_j^k\\partial \\beta_j\\cdot\\frac\\partial \\beta_j\\partial w_hj
∂whj∂Ek=∂yjk^∂Ek⋅∂βj∂yjk^⋅以上是关于神经网络--记一次西瓜书阅读的主要内容,如果未能解决你的问题,请参考以下文章