机器学习图解十大经典机器学习算法
Posted Taily老段
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习图解十大经典机器学习算法相关的知识,希望对你有一定的参考价值。
【机器学习】图解十大经典机器学习算法
决策树(Decision Tree)
根据一些 feature(特征) 进行分类,每个节点提一个问题,通过判断,将数据分为两类,再继续提问。这些问题是根据已有数据学习出来的,再投入新数据的时候,就可以根据这棵树上的问题,将数据划分到合适的叶子上。
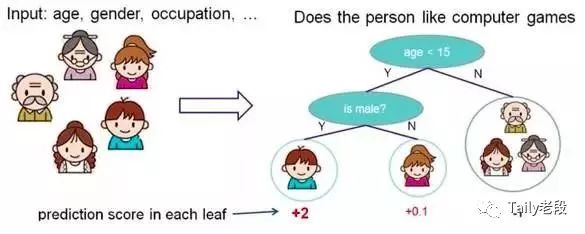
决策树原理示意图
决策树学习使用一个决策树作为一个预测模型,它将对一个 item(表征在分支上)观察所得映射成关于该 item 的目标值的结论(表征在叶子中)。
树模型中的目标是可变的,可以采一组有限值,被称为分类树;在这些树结构中,叶子表示类标签,分支表示表征这些类标签的连接的特征。
例子:
-
分类和回归树(Classification and Regression Tree,CART)
-
Iterative Dichotomiser 3(ID3)
-
C4.5 和 C5.0(一种强大方法的两个不同版本)
优点:
-
容易解释
-
非参数型
缺点:
-
趋向过拟合
-
可能或陷于局部最小值中
-
没有在线学习
随机森林(Random forest)
在源数据中随机选取数据,组成几个子集:
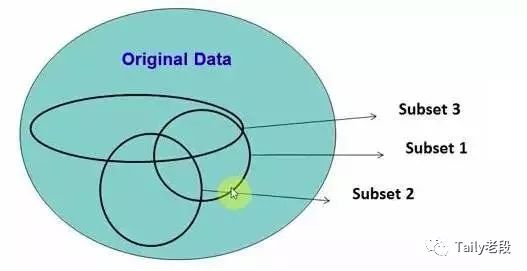
随机森林原理示意图
S矩阵是源数据,有1-N条数据,A、B、C 是feature,最后一列C是类别:
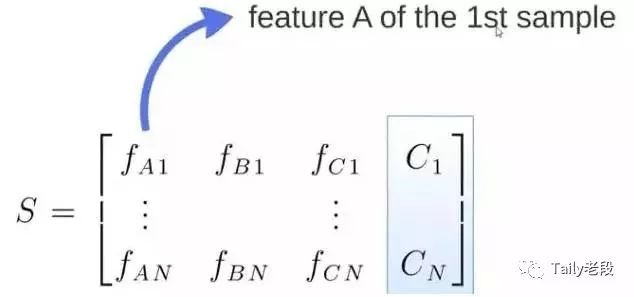
由S随机生成M个子矩阵:

这M个子集得到 M 个决策树:将新数据投入到这M个树中,得到M个分类结果,计数看预测成哪一类的数目最多,就将此类别作为最后的预测结果。
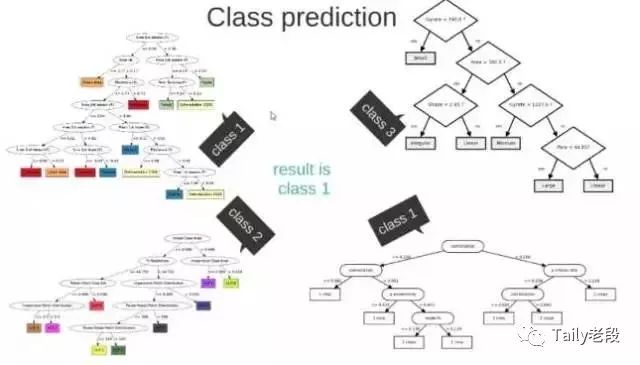
随机森林效果展示图
严格来说,随机森林其实算是一种集成算法。它首先随机选取不同的特征(feature)和训练样本(training sample),生成大量的决策树,然后综合这些决策树的结果来进行最终的分类。
随机森林在现实分析中被大量使用,它相对于决策树,在准确性上有了很大的提升,同时一定程度上改善了决策树容易被攻击的特点。
适用情景:
数据维度相对低(几十维),同时对准确性有较高要求时。
因为不需要很多参数调整就可以达到不错的效果,基本上不知道用什么方法的时候都可以先试一下随机森林。
逻辑回归(Logistic Regression)
当预测目标是概率这样的,值域需要满足大于等于0,小于等于1的,这个时候单纯的线性模型是做不到的,因为在定义域不在某个范围之内时,值域也超出了规定区间。
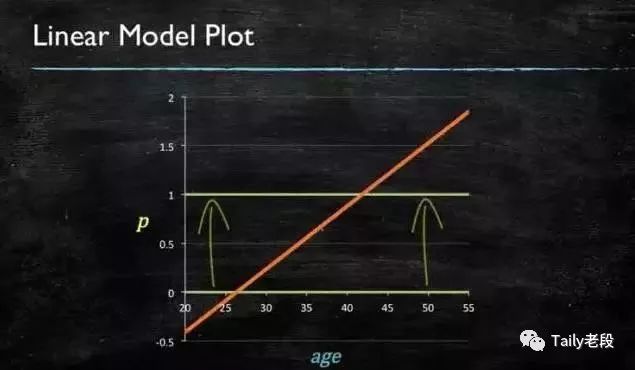
线性模型图
所以此时需要这样的形状的模型会比较好:
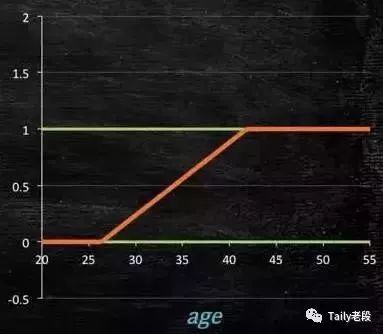
那么怎么得到这样的模型呢?
这个模型需要满足两个条件 “大于等于0”,“小于等于1” 。大于等于0 的模型可以选择绝对值,平方值,这里用指数函数,一定大于0;小于等于1 用除法,分子是自己,分母是自身加上1,那一定是小于1的了。
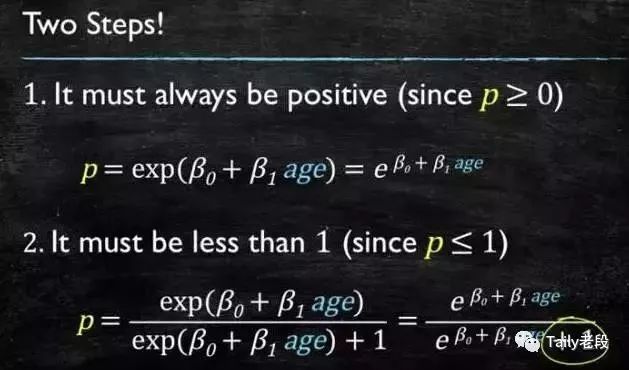
再做一下变形,就得到了 logistic regressions 模型:

通过源数据计算可以得到相应的系数了:
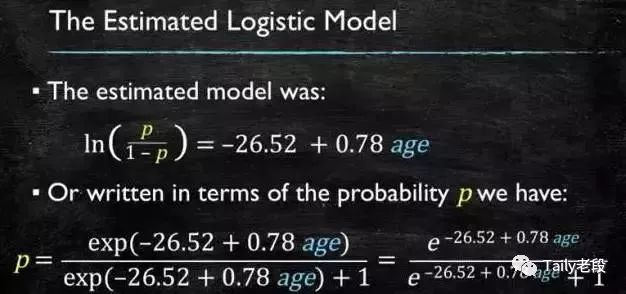
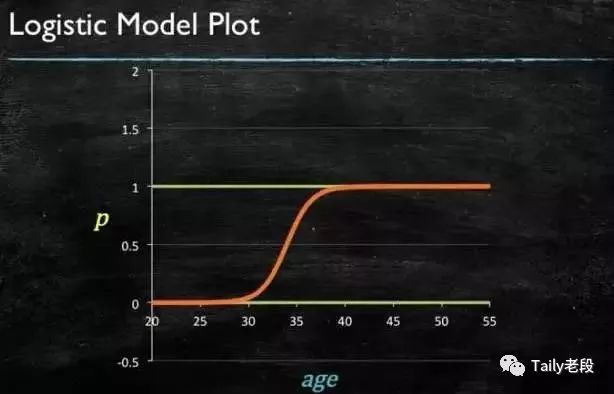
LR模型曲线图
逻辑回归这个名字太诡异了,我就叫它LR吧,反正讨论的是分类器,也没有别的方法叫LR。顾名思义,它其实是回归类方法的一个变体。
回归方法的核心就是为函数找到最合适的参数,使得函数的值和样本的值最接近。例如线性回归(Linear regression)就是对于函数f(x)=ax+b,找到最合适的a,b。
LR拟合的就不是线性函数了,它拟合的是一个概率学中的函数,f(x)的值这时候就反映了样本属于这个类的概率。
适用情景:
LR同样是很多分类算法的基础组件,它的好处是输出值自然地落在0到1之间,并且有概率意义。
因为它本质上是一个线性的分类器,所以处理不好特征之间相关的情况。
虽然效果一般,却胜在模型清晰,背后的概率学经得住推敲。它拟合出来的参数就代表了每一个特征(feature)对结果的影响。也是一个理解数据的好工具。
支持向量机(Support Vector Machines)
要将两类分开,想要得到一个超平面,最优的超平面是到两类的 margin 达到最大,margin就是超平面与离它最近一点的距离,如下图,Z2>Z1,所以绿色的超平面比较好。
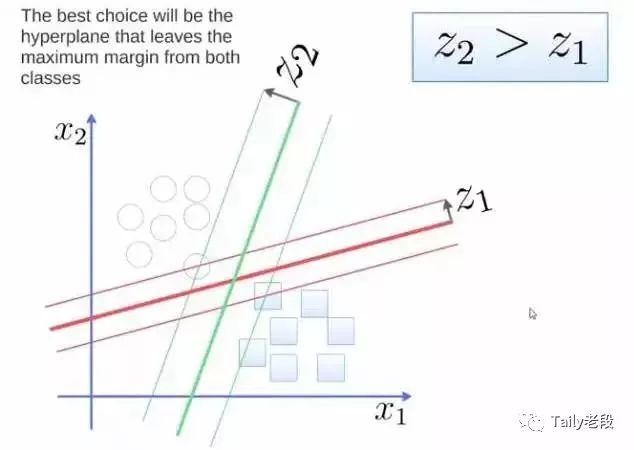
分类问题示意图
将这个超平面表示成一个线性方程,在线上方的一类,都大于等于1,另一类小于等于-1:
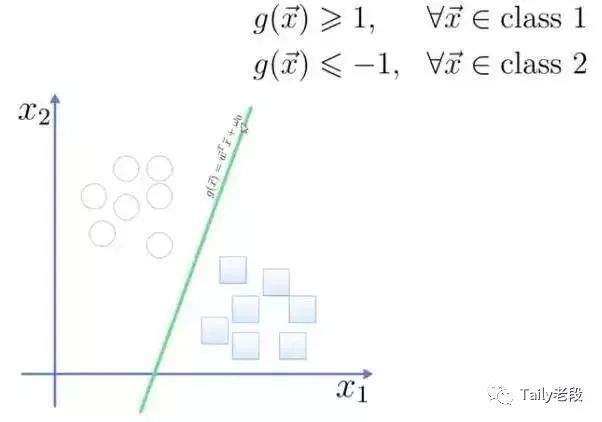
点到面的距离根据图中的公式计算:
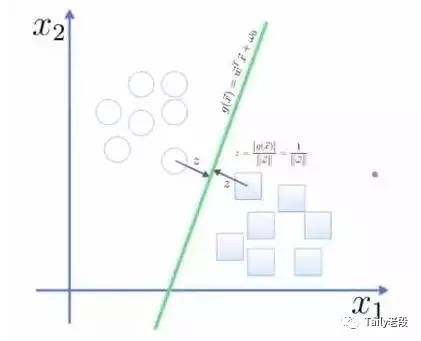
所以得到total margin的表达式如下,目标是最大化这个margin,就需要最小化分母,于是变成了一个优化问题:
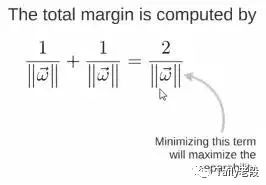
举个例子,三个点,找到最优的超平面,定义了 weight vector=(2,3)-(1,1):
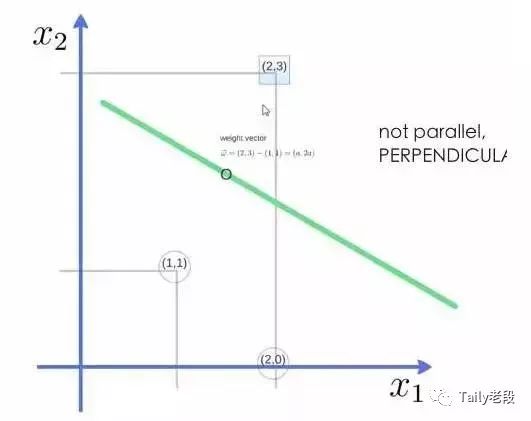
得到weight vector为(a,2a),将两个点代入方程,代入(2,3)另其值=1,代入(1,1)另其值=-1,求解出 a 和 截矩 w0 的值,进而得到超平面的表达式。
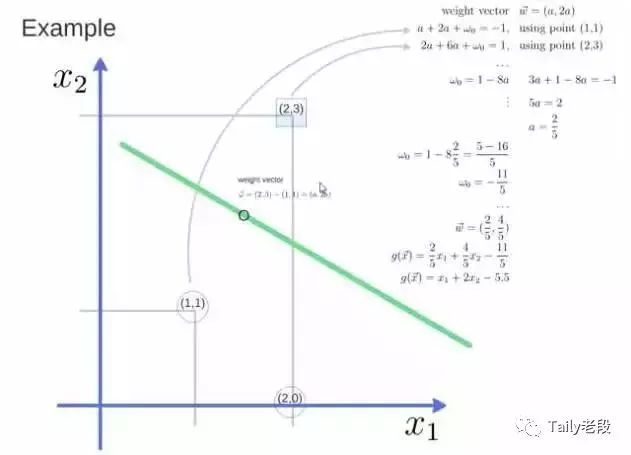
a求出来后,代入(a,2a)得到的就是support vector,a和w0代入超平面的方程就是support vector machine。
给定一组训练事例,其中每个事例都属于两个类别中的一个,支持向量机(SVM)训练算法可以在被输入新的事例后将其分类到两个类别中的一个,使自身成为非概率二进制线性分类器。
SVM 模型将训练事例表示为空间中的点,它们被映射到一幅图中,由一条明确的、尽可能宽的间隔分开以区分两个类别。
随后,新的示例会被映射到同一空间中,并基于它们落在间隔的哪一侧来预测它属于的类别。
优点:
在非线性可分问题上表现优秀
缺点:
-
非常难以训练
-
很难解释
-
朴素贝叶斯(Bayesian Algorithms)
举个在 NLP 的应用:给一段文字,返回情感分类,这段文字的态度是positive,还是negative:

图6-1 问题案例
为了解决这个问题,可以只看其中的一些单词:

这段文字,将仅由一些单词和它们的计数代表:
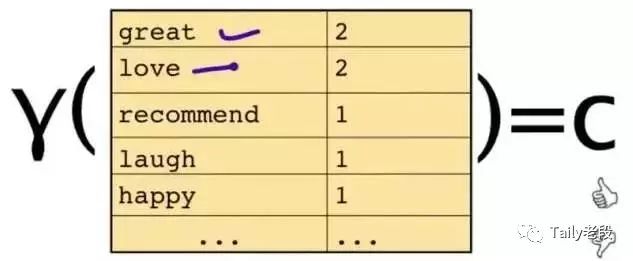
原始问题是:给你一句话,它属于哪一类 ?通过bayes rules变成一个比较简单容易求得的问题:
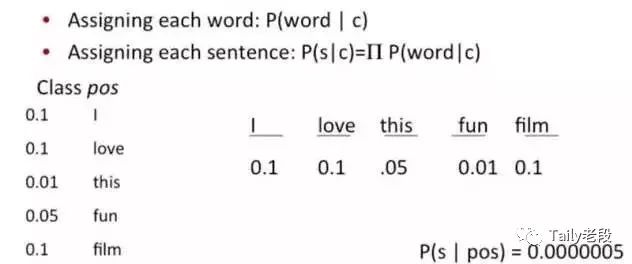
问题变成,这一类中这句话出现的概率是多少,当然,别忘了公式里的另外两个概率。例子:单词“love”在positive的情况下出现的概率是 0.1,在negative的情况下出现的概率是0.001。
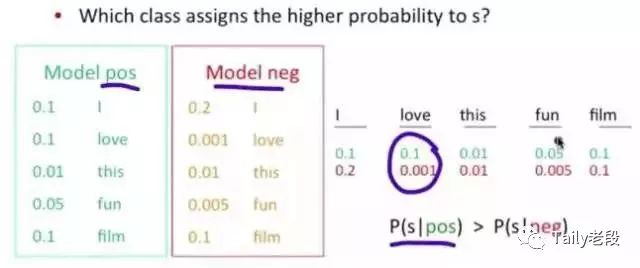
NB算法结果展示图
贝叶斯方法是指明确应用了贝叶斯定理来解决如分类和回归等问题的方法。
例子:
-
朴素贝叶斯(Naive Bayes)
-
高斯朴素贝叶斯(Gaussian Naive Bayes)
-
多项式朴素贝叶斯(Multinomial Naive Bayes)
-
平均一致依赖估计器(Averaged One-Dependence Estimators (AODE))
-
贝叶斯信念网络(Bayesian Belief Network (BBN))
-
贝叶斯网络(Bayesian Network (BN))
优点:
快速、易于训练、给出了它们所需的资源能带来良好的表现
缺点:
-
如果输入变量是相关的,则会出现问题
-
K近邻算法
给一个新的数据时,离它最近的 k 个点中,哪个类别多,这个数据就属于哪一类。
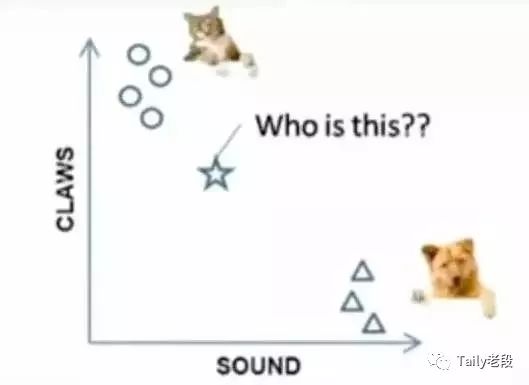
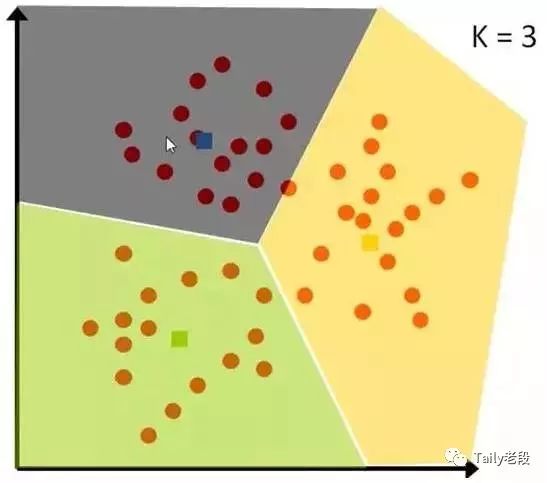
例子:要区分“猫”和“狗”,通过“claws”和“sound”两个feature来判断的话,圆形和三角形是已知分类的了,那么这个“star”代表的是哪一类呢?
问题案例
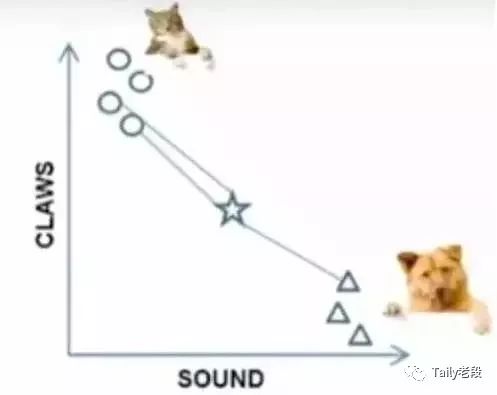
k=3时,这三条线链接的点就是最近的三个点,那么圆形多一些,所以这个star就是属于猫。
算法步骤展示图
K均值算法
先要将一组数据,分为三类,粉色数值大,黄色数值小 。最开始先初始化,这里面选了最简单的 3,2,1 作为各类的初始值 。剩下的数据里,每个都与三个初始值计算距离,然后归类到离它最近的初始值所在类别。
问题案例
分好类后,计算每一类的平均值,作为新一轮的中心点:
几轮之后,分组不再变化了,就可以停止了:


算法结果展示

Adaboost
Adaboost 是 Boosting 的方法之一。Boosting就是把若干个分类效果并不好的分类器综合起来考虑,会得到一个效果比较好的分类器。
下图,左右两个决策树,单个看是效果不怎么好的,但是把同样的数据投入进去,把两个结果加起来考虑,就会增加可信度。
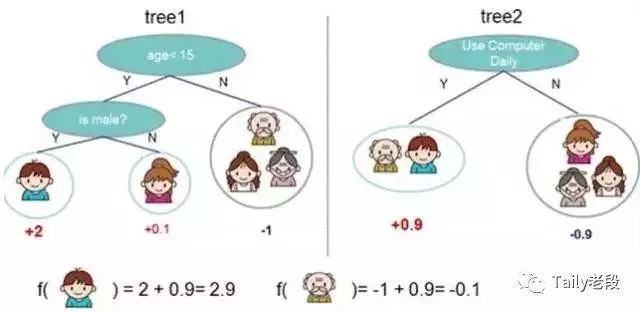
算法原理展示
Adaboost 的例子,手写识别中,在画板上可以抓取到很多features(特征),例如始点的方向,始点和终点的距离等等。
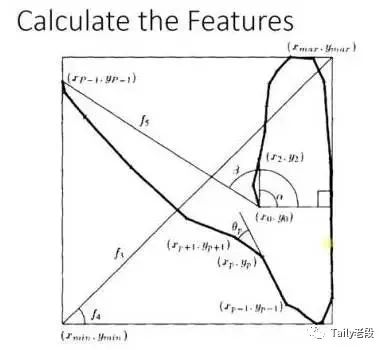
training的时候,会得到每个feature的weight(权重),例如2和3的开头部分很像,这个feature对分类起到的作用很小,它的权重也就会较小。

而这个alpha角就具有很强的识别性,这个feature的权重就会较大,最后的预测结果是综合考虑这些feature的结果。

神经网络(Neural Networks)
Neural Networks适合一个input可能落入至少两个类别里:NN由若干层神经元,和它们之间的联系组成。 第一层是input层,最后一层是output层。在hidden层和output层都有自己的classifier。
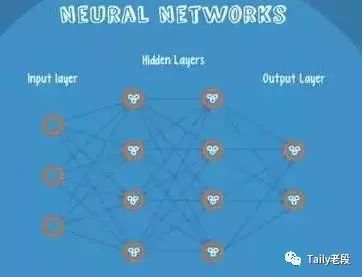
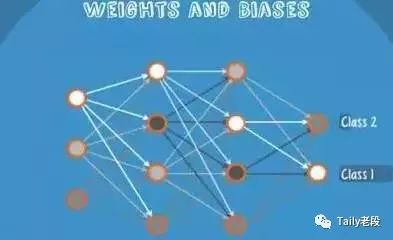
神经网络结构
input输入到网络中,被激活,计算的分数被传递到下一层,激活后面的神经层,最后output层的节点上的分数代表属于各类的分数,下图例子得到分类结果为class 1;同样的input被传输到不同的节点上,之所以会得到不同的结果是因为各自节点有不同的weights 和bias,这也就是forward propagation。
算法结果展示
人工神经网络是受生物神经网络启发而构建的算法模型。
它是一种模式匹配,常被用于回归和分类问题,但拥有庞大的子域,由数百种算法和各类问题的变体组成。
例子:
-
感知器
-
反向传播
-
Hopfield 网络
-
径向基函数网络(Radial Basis Function Network,RBFN)
优点:
-
在语音、语义、视觉、各类游戏(如围棋)的任务中表现极好。
-
算法可以快速调整,适应新的问题。
缺点:
需要大量数据进行训练
训练要求很高的硬件配置
模型处于「黑箱状态」,难以理解内部机制
元参数(Metaparameter)与网络拓扑选择困难。
马尔科夫
Markov Chains由state(状态)和transitions(转移)组成。例子,根据这一句话 ‘the quick brown fox jumps over the lazy dog’,要得到markov chains。
步骤,先给每一个单词设定成一个状态,然后计算状态间转换的概率。
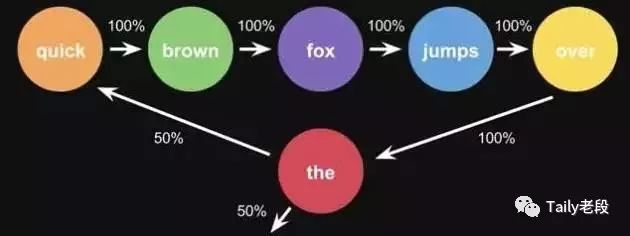
马尔科夫原理图
这是一句话计算出来的概率,当你用大量文本去做统计的时候,会得到更大的状态转移矩阵,例如the后面可以连接的单词,及相应的概率。
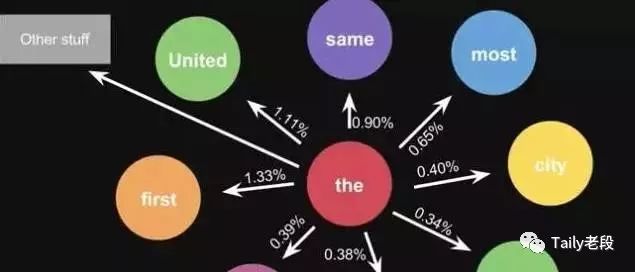
算法结果展示
上述十大类机器学习算法是人工智能发展的践行者,即使在当下,依然在数据挖掘以及小样本的人工智能问题中被广泛使用。
Taily老段的微信公众号,欢迎交流学习

以上是关于机器学习图解十大经典机器学习算法的主要内容,如果未能解决你的问题,请参考以下文章