二分图最大匹配--匈牙利算法

Posted 2022-12-06 如风如影�

嗑cp(二分图最大匹配–匈牙利算法）

题目链接: link.

题目描述
Alice喜欢嗑cp，她总是幻想她喜欢的男明星可以和她喜欢的女明星处cp， 已知n个男，m个女（男明星编号从1到n，女明星编号1到m），k组有可能发展成cp关系的组合， 一个人最多只能和一名异性处cp，Alice想知道她最多能嗑几组cp？
Input
第一行输入三个整数n,m,k（1<=n,m<=500,1<=k<=5e4），分别表示男明星个数，女明星个数，和有可能发展成cp的组合。接下来输入k行，每行两个整数u,v(1<=u<=n,1<=v<=m)表示编号为编号为u的男与编号为v的女可能成为cp。
output
输出一个整数，表示Alice最多能嗑几组cp。

样例

输入
2 3 4
1 1
1 3
2 1
2 2

 输出
 2

提示
由题意看，考察的是二分图最大匹配问题，先看下二分图。

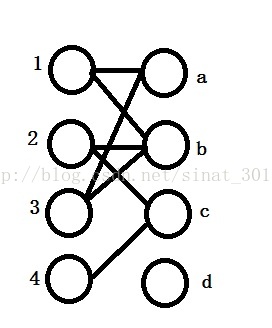
把左边1，2，3，4和右边a,b,c,d来进行匹配。由该二分图可以看出，每个人的选择有多种且会冲突，所以会有一个最大匹配问题，这就用到了匈牙利算法。

匈牙利算法大概思路就是，遍历左面的男生，然后扫描右面的妹子，如果有情投意合的并且该妹子还没有被别人占有，那么这个妹子就归属当前这个男生，若是被别人占有，那么尝试给占有她的那个男生重新分配一个，通俗点就是想办法给这个男生腾出一个妹子，若是没有办法实现的话，那便无能为力了。

#include <bits/stdc++.h>
using namespace std;
const int N=501;
int a[N][N],g[N],mi[N];//a数组存放情投意合的组合,g数组记录妹子被哪个男生占有,mi数组记录有没有尝试为他重新找一个
int n,m,k;
bool find(int x)

    for(int j=1;j<=m;j++)//扫描每个妹子
    
        if(a[x][j]==1&&mi[j]==0)//如果情投意合且之前没有尝试重新组合（也就是之前尝试改变过，但是没有成功，就不用浪费时间了）
        
            mi[j]=1;
            if(g[j]==0||find(g[j])==true)//如果妹子没有主或者可以为他的主重新分配一个
            
                g[j]=x;
                return true;
            
        
    
    return false;

int main()

    cin>>n>>m>>k;
    memset(a,0,sizeof(a));
    memset(g,0,sizeof(g));
    for(int i=1;i<=k;i++)
    
        int x,y;
        cin>>x>>y;
        a[x][y]=1;
    
    int h=0;
    for(int i=1;i<=n;i++)//遍历每个男生
    
        memset(mi,0,sizeof(mi));
        if(find(i)==true) h++;
    
    cout<<h<<endl;
    return 0;