动态规划-第一节3：动态规划之使用“找零钱”问题说明最优子结构如何解决

Posted 2022-12-06 我擦我擦

• 注意：本文参考labuladong总结
• 链接

文章目录

• • （1）什么是最优子结构
  • （2）暴力解法
  • （2）带有表的递归解法
  • （3）动态规划解法

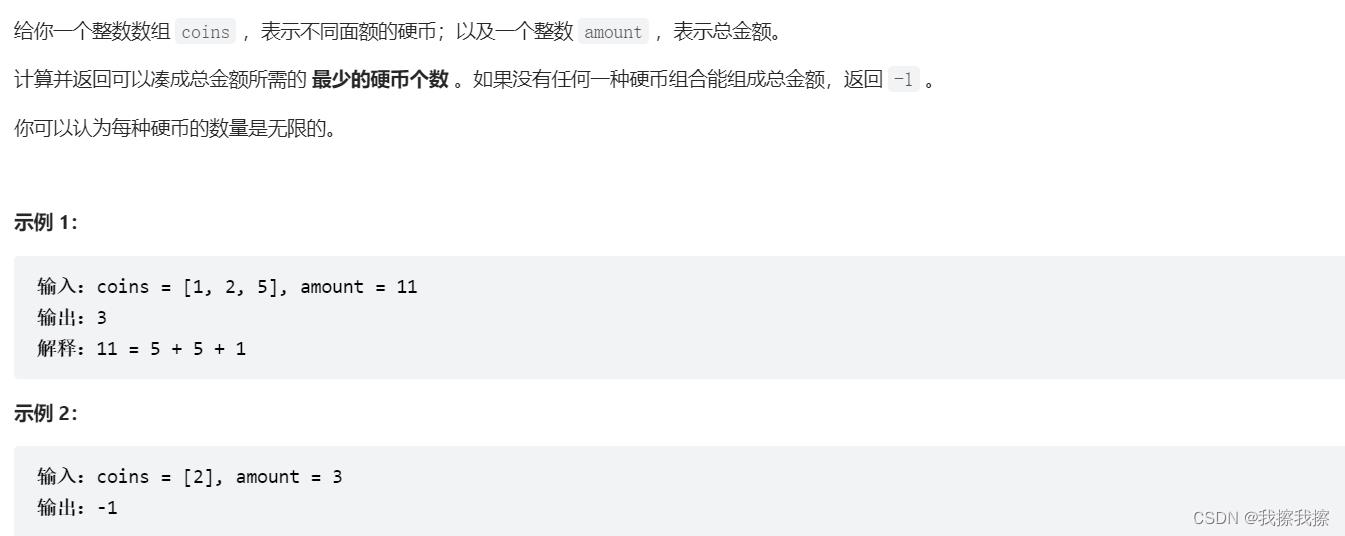
前文说过，动态规划所要解决的问题必须具有最优子结构，什么是最优子结构以及如何处理，我们将通过 lLeetCode 509：零钱兑换这道题进行说明

（1）什么是最优子结构

最优子结构：最优子结构是某些问题的一种特定性质，并不是动态规划问题专有的。也就是说，很多问题其实都具有最优子结构，只是其中大部分不具有重叠子问题，所以我们不把它们归为动态规划系列问题而已

举一个简单的例子：假设你们学校有 10 个班，你已经计算出了每个班的最高考试成绩。那么现在我要求你计算全校最高的成绩，你会不会算？当然会，而且你不用重新遍历全校学生的分数进行比较，而是只要在这 10 个最高成绩中取最大的就是全校的最高成绩

这个例子就符合最优子结构：可以从子问题的最优结果推出更大规模问题的最优结果。让你算每个班的最优成绩就是子问题，你知道所有子问题的答案后，就可以借此推出全校学生的最优成绩这个规模更大的问题的答案

这么简单的问题都有最优子结构性质，只是因为显然没有重叠子问题，所以我们简单地求最值肯定用不出动态规划。而一旦有重叠子问题，就没有那么容易看出答案了

再举一个例子：假设你们学校有 10 个班，你已知每个班的最大分数差（最高分和最低分的差值）。那么现在我让你计算全校学生中的最大分数差，你会不会算？可以想办法算，但是肯定不能通过已知的这 10 个班的最大分数差推到出来。因为这 10 个班的最大分数差不一定就包含全校学生的最大分数差，比如全校的最大分数差可能是 3 班的最高分和 6 班的最低分之差

这个例子就不符合最优子结构，因为你没办通过每个班的最优值推出全校的最优值，没办法通过子问题的最优值推出规模更大的问题的最优值

回到凑零钱的问题来，它就很好的满足了最优子结构。以下面这个例子为例

你想要解决“如何以最少的硬币凑够11元”的问题，那么那就需要先解决“如何以最少的硬币凑够10元”的子问题，因为一旦满足刚才的子问题，只需要加上一块硬币（面值为1）就能解决终极问题了

（2）暴力解法

前文说过，暴力解法对应的就是状态转移方程，这也是每个题目最难的地方。所以在写状态转移方程时你应该考虑以下几点

• 最简单的情况是什么：此题很显然使目标金额如果为0，就让程序返回0，此时不需要任何硬币就可以凑出目标金额了
• 这个问题有什么状态？也就是是原问题和子问题中会变化的量：也很简单，硬币数量无限，但金额数是在不断变化的，不断向最简单情况靠近，所以状态是目标金额amount
• 每个状态可以做怎样的选择使得状态变化：很明显，选择硬币时，硬币的面额会减少目标金额，所以硬币的面额就是选择
• 明确表的定义：动态规划就是一个不断填表的过程。定义table(n) 为，输入一个目标金额 n，返回凑出目标金额 n 所需的最少硬币数量

根据以上思想，写出暴力递归代码如下

class Solution 
public:
    int dp(vector<int> &coins, int n)
        //最简单情况
        if(n == 0) return 0;//如果n为0，那么就不需要硬币
        if(n < 0) return -1;//如果n<0，表示这种选取方案失败
        int res = INT_MAX;
        for(size_t i = 0; i < coins.size(); i++)
            //选择一块硬币，面额为coins[i]，还需要凑够n-coins[i]
            int subproblem = dp(coins, n - coins[i]);
            //如果返回-1，表示选择conis[i]不可取，那么就继续下一个面额
            if(subproblem == -1)
                continue;
            
            //始终保持最小
            res = min(res, 1+subproblem);
        
        if(res!=INT_MAX)
            return res;
        else
            return -1;
        

     

    int coinChange(vector<int>& coins, int amount) 
        return dp(coins, amount);
    
;

当然这道题是无法通过的，因为暴力解法时间复杂度太大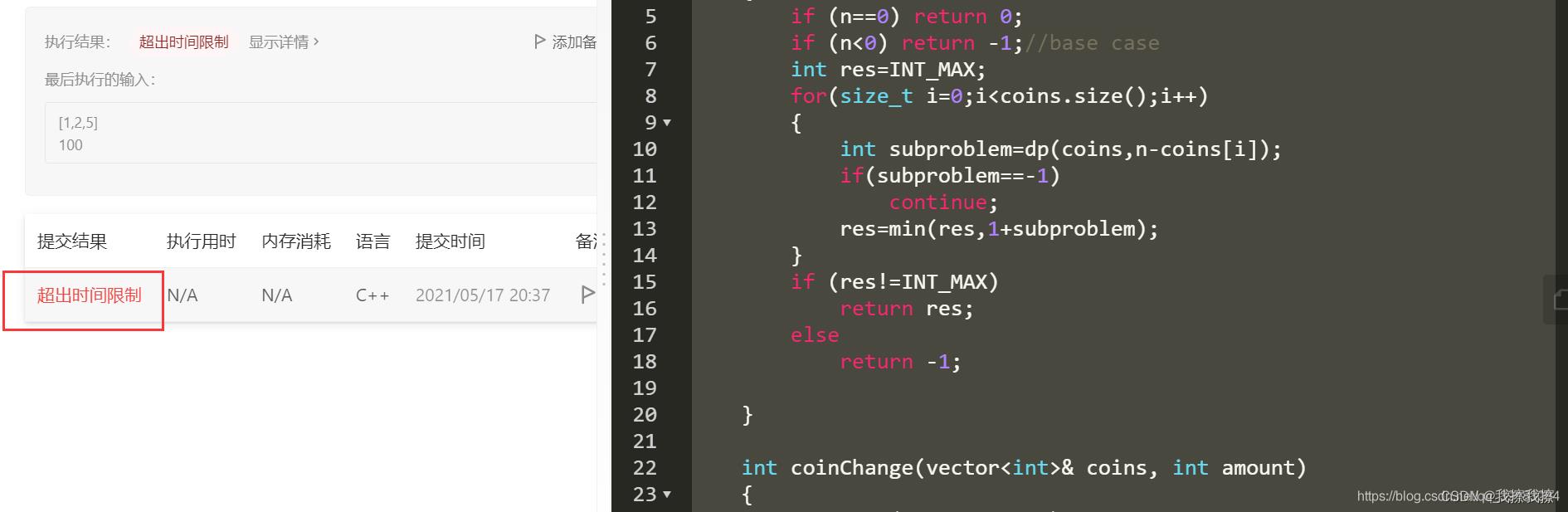

画出递归树，就可以看见很多重叠子问题没有解决

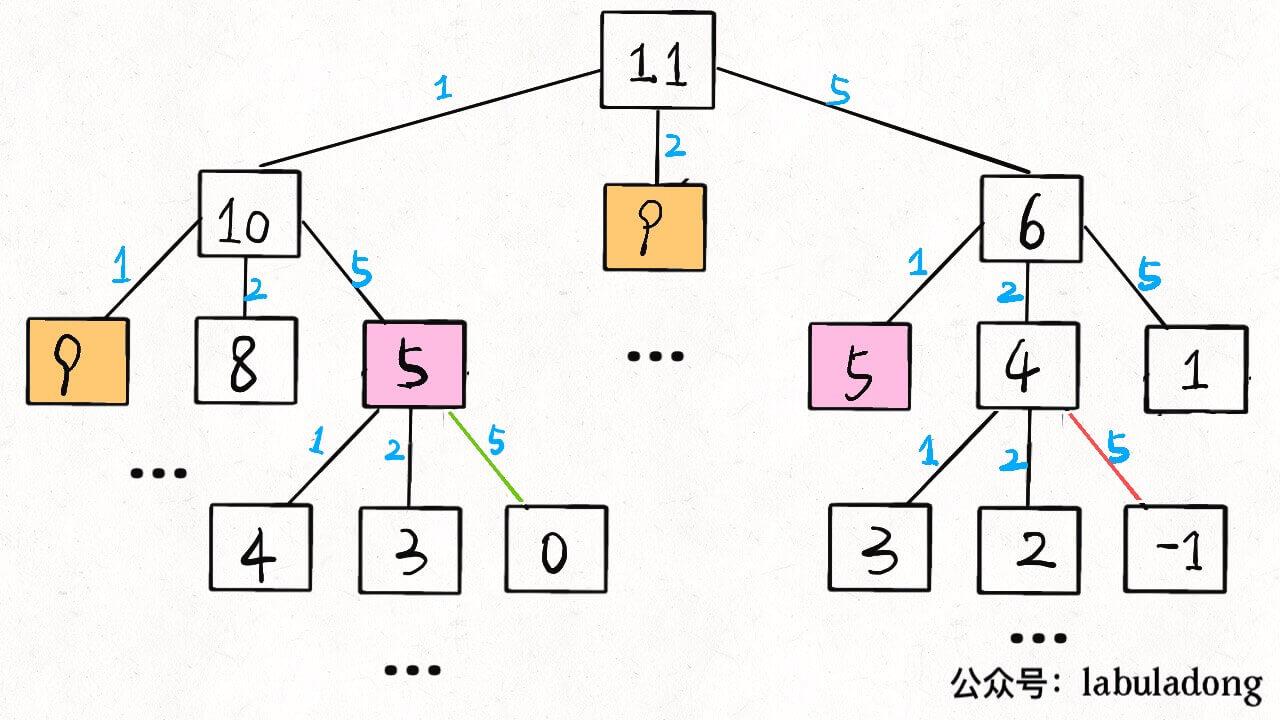
（2）带有表的递归解法

为了降低时间复杂度，我们建立一张表，记录重叠子问题

class Solution 
public:
    int dp(vector<int> &coins, int n, vector<int> &table)
        //最简单情况
        if(n == 0) return 0;//如果n为0，那么就不需要硬币
        if(n < 0) return -1;//如果n<0，表示这种选取方案失败
        //如果表里有值直接拿
        if(table[n] != -1000)
            return table[n];
        
        int res = INT_MAX;
        for(size_t i = 0; i < coins.size(); i++)
            //选择一块硬币，面额为coins[i]，还需要凑够n-coins[i]
            int subproblem = dp(coins, n - coins[i], table);
            //如果返回-1，表示选择conis[i]不可取，那么就继续下一个面额
            if(subproblem == -1)
                continue;
            
            //始终保持最小
            res = min(res, 1+subproblem);
        
        //记录在表
        if(res!=INT_MAX)
            table[n] = res;
        else
            table[n] = -1;
        
        return table[n];
     

    int coinChange(vector<int>& coins, int amount) 
        //建立一张表，初始化为一个不会取到的值，代表没有存放
        vector<int> table(amount+1, -1000);
        return dp(coins, amount, table);
    
;

可以通过

（3）动态规划解法

class Solution 
public:
    int coinChange(vector<int>& coins, int amount) 
        //建立一张表，面额为amount最多需要among块硬币
        vector<int> table(amount+1, amount+1);
        //最简单情况，面额为0需要0块硬币
        table[0] = 0;

        for(int i = 0; i < table.size(); i++)
            //外层循环是状态，就是面额为i时的硬币数量table[i]
            for(auto coin : coins)
                if(i-coin < 0)
                    //无解
                    continue;
                
                table[i] = min(table[i], 1+table[i-coin]);
            
           

        if(table[amount] == amount+1)
            return -1;
        else
            return table[amount];
        
    
;