DBSCAN聚类算法的实现

Posted 2022-12-06 ZHW_AI课题组

DBSCAN聚类算法的实现

• 1. 作者介绍
• 2.关于理论方面的知识介绍
• • 2.1 DBSCAN算法介绍
  • 2.2 鸢尾花数据集介绍
• 3．实验过程
• • 3.1 实验代码
  • 3.2 实现过程
  • 3.3 实验结果
• 4．参考文献

1. 作者介绍

刘鹏程，男，西安工程大学电子信息学院，2021级硕士研究生
研究方向：机器视觉与人工智能
电子邮件：[e-mail]

孟莉苹，女，西安工程大学电子信息学院，2021级硕士研究生，张宏伟人工智能课题组
研究方向：机器视觉与人工智能
电子邮件：[e-mail]

2.关于理论方面的知识介绍

2.1 DBSCAN算法介绍

DBSCAN（Density—Based Spatial Clustering of Application with Noise）算法是一种典型的基于密度的聚类方法。它将簇定义为密度相连的点的最大集合，能够把具有足够密度的区域划分为簇，并可以在有噪音的空间数据集中发现任意形状的簇。
1. 基本概念
DBSCAN 算法中有两个重要参数：Eps和MmPtS。Eps是定义密度时的邻域半径，MmPts 为定义核心点时的阈值。
在DBSCAN算法中将数据点分为以下3类：
1）核心点
如果一个对象在其半径Eps内含有超过MmPts数目的点，则该对象为核心点。
2）边界点
如果一个对象在其半径Eps内含有点的数量小于MinPts，但是该对象落在核心点的邻域内，则该对象为边界点。
3）噪音点
如果一个对象既不是核心点也不是边界点，则该对象为噪音点。
通俗地讲，核心点对应稠密区域内部的点，边界点对应稠密区域边缘的点，而噪音点对应稀疏区域中的点。
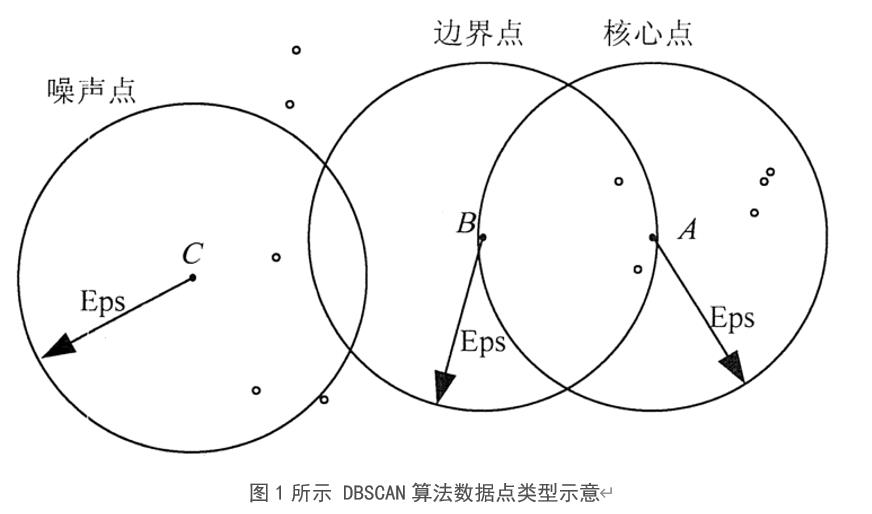
在图1中，假设MinPts=5，Eps如图中箭头线所示，则点A为核心点，点B 为边界点，点C为噪音点。点A因为在其Eps邻域内含有7个点，超过了Eps=5，所以是核心点。
点E和点C因为在其Eps邻域內含有点的个数均少于5，所以不是核心点；点B因为落在了点A的Eps邻域内，所以点B是边界点；点C因为没有落在任何核心点的邻域内，所以是噪音点。

进一步来讲，DBSCAN算法还涉及以下一些概念。

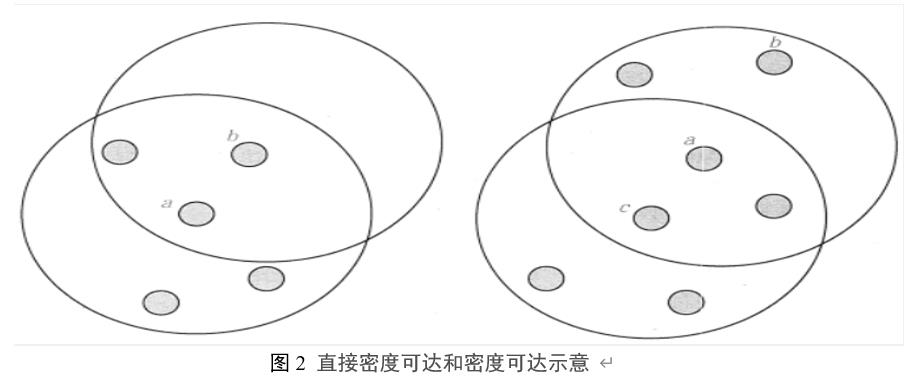
在图2中，点a为核心点，点b为边界点，并且因为a直接密度可达b。但是b不直接密度可达a(因为b不是一个核心点)。因为c直接密度可达a，a直接密度可达b，所以c密度可达b。但是因为b不直接密度可达a，所以b不密度可达c。但是b和c密度相连。
2.算法描述
DBSCAN算法对簇的定义很简单，由密度可达关系导出的最大密度相连的样本集合，即为最终聚类的一个簇。
DBSCAN算法的簇里面可以有一个或者多个核心点。如果只有一个核心点，则簇里其他的非核心点样本都在这个核心点的Eps邻域里。如果有多个核心点，则簇里的任意一个核心点的Eps邻域中一定有一个其他的核心点，否则这两个核心点无法密度可达。这些核心点的Eps邻域里所有的样本的集合组成一个DBSCAN 聚类簇。
DBSCAN算法的描述如下：
1)输入：数据集，邻域半径Eps，邻域中数据对象数目阈值MinPts;
2)输出：密度联通簇。
处理流程如下。
1)从数据集中任意选取一个数据对象点p；
2)如果对于参数Eps和MinPts，所选取的数据对象点p为核心点，则找出所有从p密度可达的数据对象点，形成一个簇；
3)如果选取的数据对象点p是边缘点，选取另一个数据对象点；
4)重复(2)、(3)步，直到所有点被处理。
DBSCAN算法的计算复杂的度为O(n²)，n为数据对象的数目。这种算法对于输入参数Eps和MinPts是敏感的。
**3.算法实例
下面给出一个样本数据集，如表1所示，并对其实施DBSCAN算法进行聚类，取 Eps=3，MinPts=3。

数据集中的样本数据在二维空间内的表示如图 3 所示：

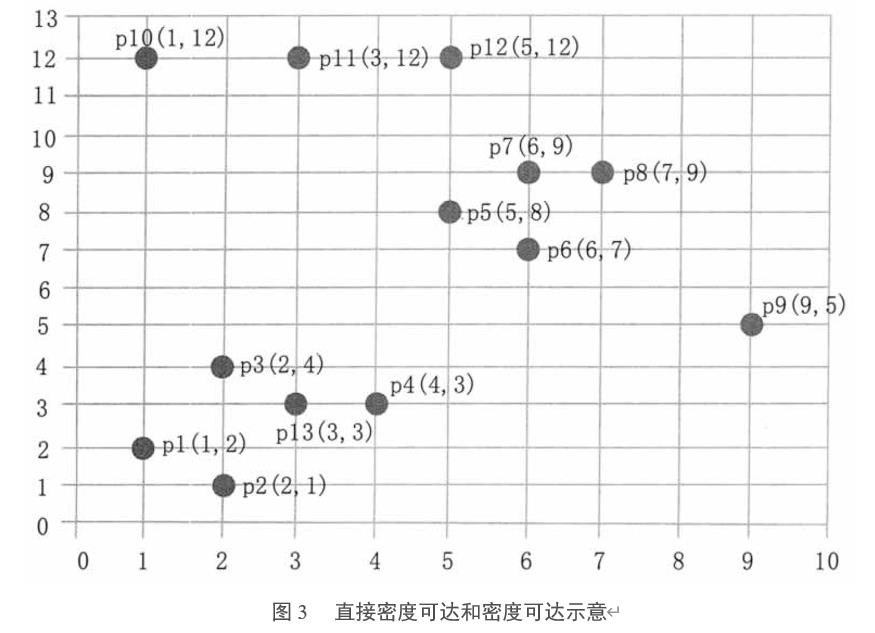
第一步： 顺序扫描数据集的样本点，首先取到p1(1,2)。

1. 计算p1的领域，计算出每一点到p1的距离，如d(p1,p2)=sqrt(1+1)=1.414。
2. 根据每个样本点到p1的距离，计算出p1的Eps领域为p1,p2,p3,p13。
3. 因为p1的Eps邻域含有4个点，大于 MinPts(3)，所以，p1 为核心点。
4. 以p1为核心点建立簇C1，即找出所有从p1密度可达的点。
5. p1邻域内的点都是p1直接密度可达的点，所以都属于C1。
6. 寻找p1密度可达的点，p2的邻域为p1,p2,p3,p4,p13，因为p1密度可达p2，p2密度可达p4，所以p1密度可达p4，因此p4也属于C1。
7. p3的邻域为p1,p2,p3,p4,p13，p13的邻域为p1,p2,p3,p4,p13，p3和p13 都是核心点，但是它们邻域的点都已经在Cl中。
8. P4的邻域为p3,p4,p13，为核心点，其邻域内的所有点都已经被处理。
9. 此时，以p1为核心点出发的那些密度可达的对象都全部处理完毕，得到簇C1，包含点p1,p2,p3,p13,p4。
   第二步： 继续顺序扫描数据集的样本点，取到p5(5,8)。
10. 计算p5的领域，计算出每一点到p5的距离，如d(p1,p8)=sqrt(4+1)=2.236。
11. 根据每个样本点到p5的距离，计算出p5的Eps邻域为p5,p6,p7,p8。
12. 因为p5的Eps邻域含有4个点，大于MinPts(3)，所以，p5为核心点。
13. 以p5为核心点建立簇C2，即找出所有从p5密度可达的点，可以获得簇 C2，包含点p5,p6,p7,p8。
    第三步： 继续顺序扫描数据集的样本点，取到p9(9,5)。
14. 计算出p9的Eps领域为p9，个数小于MinPts(3)，所以p9不是核心点。
15. 对p9处理结束。
    第四步： 继续顺序扫描数据集的样本点，取到p10(1,12)。
16. 计算出p10的Eps邻域为p10,p11，个数小于MinPts(3)，所以p10不是核心点。
17. 对p10处理结束。
    第五步： 继续顺序扫描数据集的样本点，取到p11(3,12)。
18. 计算出p11的Eps邻域为p11,p10,p12，个数等于MinPts(3)，所以p11是核心点。
19. 从p12的邻域为p12,p11，不是核心点。
20. 以p11为核心点建立簇C3，包含点p11,p10,p12。
    第六步： 继续扫描数据的样本点，p12、p13都已经被处理过，算法结束。

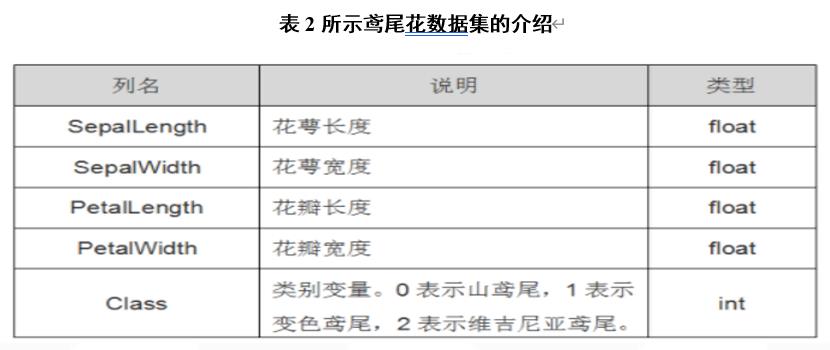
2.2 鸢尾花数据集介绍

Iris数据集是常用的分类实验数据集，由Fisher, 1936收集整理。Iris也称鸢尾花卉数据集，是一类多重变量分析的数据集。本实验所用到的数据集为iris鸢尾花数据集，Iris鸢尾花数据集内包含3类分别为山鸢尾(Iris-setosa)、变色鸢尾(Iris-versicolor)和维吉尼亚鸢尾(Iris-virginica)，共150条记录，每类各50个数据，每条记录都有4项特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度，iris以鸢尾花的特征作为数据来源，常用在分类操作中。该数据集由3种不同类型的鸢尾花的50个样本数据构成。其中的一个种类与另外两个种类是线性可分离的，后两个种类是非线性可分离的。如下表2所示：

其相对应的鸢尾花分类结果如图4所示：

3．实验过程

3.1 实验代码

#!/usr/bin/env python3
#-*- coding:utf-8 -*-
import matplotlib.pyplot as plt # 导入matplotlib的库
import numpy as np # 导入numpy的包
from sklearn.cluster import KMeans # 引入KMeans模块
from sklearn import datasets #导入数据集
from sklearn import metrics # 调用评价指标
iris = datasets.load_iris() # 导入鸢尾花数据集
X = iris.data[:, :4]  # #表示我们取特征空间中的4个维度
print(X.shape) # 打印出X的尺寸大小

#绘制数据分布图
plt.figure() # 创建图像
plt.subplot(2, 2, 1) # subplot创建单个子图，单个字图中包含4个区域，相应区域在左上角。
plt.scatter(X[:, 0], X[:, 1], c="red", marker='o', label='datas') # 画散点图
plt.xlabel('datas') # 设置X轴的标签为datas
plt.legend(loc=2) # 设置图标
#K-means
print("===K-means聚类===")
estimator = KMeans(n_clusters=3).fit(X)  # 构造聚类器
label_pred = estimator.labels_  # 获取聚类标签
#绘制k-means结果
plt.subplot(2, 2, 2) # subplot创建单个子图，单个子图中包含4个区域，相应区域在右上角。
x0 = X[label_pred == 0]# 获取聚类标签等于0的话，则赋值给x0
x1 = X[label_pred == 1]# 获取聚类标签等于1的话，则赋值给x1
x2 = X[label_pred == 2]# 获取聚类标签等于2的话，则赋值给x2
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label0')#画label0的散点图
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label1')#画label1的散点图
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label2')#画label2的散点图
plt.xlabel('K-means')# 设置X轴的标签为K-means
plt.legend(loc=2)# 设置图标在左上角
score1 = metrics.silhouette_score(X, label_pred, metric="euclidean")# 使用轮廓系数
print(score1)# 打印出轮廓系数

#密度聚类之DBSCAN算法
print("===DBSCAN聚类===")
from sklearn.cluster import DBSCAN # 引入DBSCAN模块
from sklearn import metrics # 调用评价指标
dbscan = DBSCAN(eps=0.4, min_samples=9).fit(X) #导入DBSCAN模块进行训练
label_pred = dbscan.labels_ # labels为每个数据的簇标签
plt.subplot(2, 2, 3) # 创建单个子图，单个子图中包含4个区域，相应的区域在左下角。
x0 = X[label_pred == 0] # 获取聚类标签等于0的话，则赋值给x0
x1 = X[label_pred == 1] # 获取聚类标签等于1的话，则赋值给x1
x2 = X[label_pred == 2] # 获取聚类标签等于2的话，则赋值给x2
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label0') # 画label0的散点图
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label1') # 画label1的散点图
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label2') # 画label2的散点图
plt.xlabel('DBSCAN')# 设置X轴的标签为DBSCAN
plt.legend(loc=2)# 设置图标在左上角
score = metrics.silhouette_score(X, label_pred, metric="euclidean")# 使用轮廓系数
print(score)# 打印出轮廓系数

#结构性聚类(层次聚类)
print("===层次聚类===")
from sklearn.cluster import AgglomerativeClustering # 导入AGNES算法
import pandas as pd
from sklearn.metrics import confusion_matrix # 导入混淆矩阵的指标

iris = datasets.load_iris()
irisdata = iris.data
clustering = AgglomerativeClustering(linkage='ward', n_clusters=3) # 使用层次聚类模块
res = clustering.fit(irisdata) # 用训练器数据拟合分类器模型

print("各个簇的样本数目：")
print(pd.Series(clustering.labels_).value_counts()) # 确定数据出现的频率
print("聚类结果：")
print(confusion_matrix(iris.target, clustering.labels_)) # 打印出混淆矩阵

plt.subplot(2, 2, 4) # 创建单个子图，单个子图中包含4个区域，相应的区域在右下角。
d0 = irisdata[clustering.labels_ == 0] # 获取聚类标签等于0的话，则赋值给d0
plt.plot(d0[:, 0], d0[:, 1], 'o', c="red")
d1 = irisdata[clustering.labels_ == 1] # 获取聚类标签等于1的话，则赋值给d1
plt.plot(d1[:, 0], d1[:, 1], '*', c="green")
d2 = irisdata[clustering.labels_ == 2] # 获取聚类标签等于2的话，则赋值给d2
plt.plot(d2[:, 0], d2[:, 1], '+', c="blue")
plt.xlabel("AGNES")
score2 = metrics.silhouette_score(irisdata, clustering.labels_, metric="euclidean")# 使用轮廓系数
print(score2)# 打印出轮廓系数
plt.show()

3.2 实现过程

1. 导入实验环境所需要的包

r#!/usr/bin/env python3
#-*- coding:utf-8 -*-
import matplotlib.pyplot as plt # 导入matplotlib的库
import numpy as np # 导入numpy的包
from sklearn.cluster import KMeans # 引入KMeans模块
from sklearn import datasets #导入数据集
from sklearn import metrics # 调用评价指标

2. 导入实验所需的iris鸢尾花数据集并提取维度

iris = datasets.load_iris() # 导入鸢尾花数据集
X = iris.data[:, :4]  # #表示我们取特征空间中的4个维度
print(X.shape) # 打印出X的尺寸大小

3. 绘制数据分布图

#绘制数据分布图
plt.figure() # 创建图像
plt.subplot(2, 2, 1) # subplot创建单个子图，单个字图中包含4个区域，相应区域在左上角。
plt.scatter(X[:, 0], X[:, 1], c="red", marker='o', label='datas') # 画散点图
plt.xlabel('datas') # 设置X轴的标签为datas
plt.legend(loc=2) # 设置图标

4. DBSCAN密度聚类算法

#密度聚类之DBSCAN算法
print("===DBSCAN聚类===")
from sklearn.cluster import DBSCAN # 引入DBSCAN模块
from sklearn import metrics # 调用评价指标
dbscan = DBSCAN(eps=0.4, min_samples=9).fit(X) #导入DBSCAN模块进行训练
label_pred = dbscan.labels_ # labels为每个数据的簇标签
plt.subplot(2, 2, 3) # 创建单个子图，单个子图中包含4个区域，相应的区域在左下角。
x0 = X[label_pred == 0] # 获取聚类标签等于0的话，则赋值给x0
x1 = X[label_pred == 1] # 获取聚类标签等于1的话，则赋值给x1
x2 = X[label_pred == 2] # 获取聚类标签等于2的话，则赋值给x2
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label0') # 画label0的散点图
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label1') # 画label1的散点图
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label2') # 画label2的散点图
plt.xlabel('DBSCAN')# 设置X轴的标签为DBSCAN
plt.legend(loc=2)# 设置图标在左上角
score = metrics.silhouette_score(X, label_pred, metric="euclidean")# 使用轮廓系数
print(score)# 打印出轮廓系数

5. K-means算法

#K-means
print("===K-means聚类===")
estimator = KMeans(n_clusters=3).fit(X)  # 构造聚类器
label_pred = estimator.labels_  # 获取聚类标签
#绘制k-means结果
plt.subplot(2, 2, 2) # subplot创建单个子图，单个子图中包含4个区域，相应区域在右上角。
x0 = X[label_pred == 0]# 获取聚类标签等于0的话，则赋值给x0
x1 = X[label_pred == 1]# 获取聚类标签等于1的话，则赋值给x1
x2 = X[label_pred == 2]# 获取聚类标签等于2的话，则赋值给x2
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label0')#画label0的散点图
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label1')#画label1的散点图
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label2')#画label2的散点图
plt.xlabel('K-means')# 设置X轴的标签为K-means
plt.legend(loc=2)# 设置图标在左上角
score1 = metrics.silhouette_score(X, label_pred, metric="euclidean")# 使用轮廓系数
print(score1)# 打印出轮廓系数

6. 结构性聚类算法

#结构性聚类(层次聚类)
print("===层次聚类===")
from sklearn.cluster import AgglomerativeClustering # 导入AGNES算法
import pandas as pd
from sklearn.metrics import confusion_matrix # 导入混淆矩阵的指标

iris = datasets.load_iris()
irisdata = iris.data
clustering = AgglomerativeClustering(linkage='ward', n_clusters=3) # 使用层次聚类模块
res = clustering.fit(irisdata) # 用训练器数据拟合分类器模型

print("各个簇的样本数目：")
print(pd.Series(clustering.labels_).value_counts()) # 确定数据出现的频率
print("聚类结果：")
print(confusion_matrix(iris.target, clustering.labels_)) # 打印出混淆矩阵

plt.subplot(2, 2, 4) # 创建单个子图，单个子图中包含4个区域，相应的区域在右下角。
d0 = irisdata[clustering.labels_ == 0] # 获取聚类标签等于0的话，则赋值给d0
plt.plot(d0[:, 0], d0[:, 1], 'o', c="red")
d1 = irisdata[clustering.labels_ == 1] # 获取聚类标签等于1的话，则赋值给d1
plt.plot(d1[:, 0], d1[:, 1], '*', c="green")
d2 = irisdata[clustering.labels_ == 2] # 获取聚类标签等于2的话，则赋值给d2
plt.plot(d2[:, 0], d2[:, 1], '+', c="blue")
plt.xlabel("AGNES")
score2 = metrics.silhouette_score(irisdata, clustering.labels_, metric="euclidean")# 使用轮廓系数
print(score2)# 打印出轮廓系数
plt.show()

3.3 实验结果

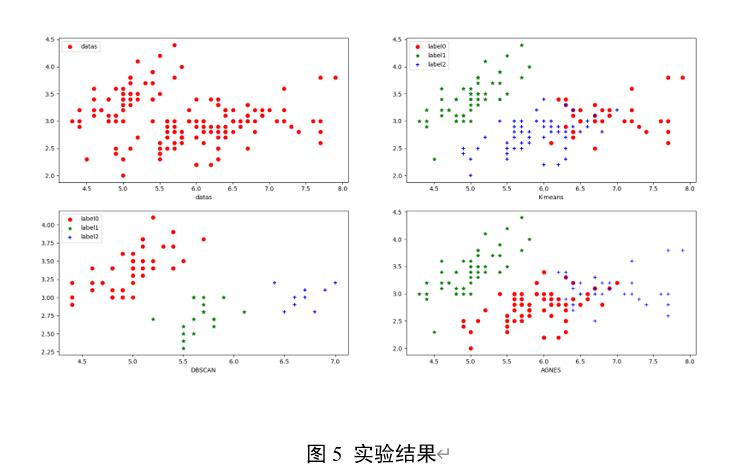
从图5实验结果可以看出，AGNES(层次聚类)没有相应再分配能力，所以算法聚类效果不好；K-means算法由于对离群点和孤立点敏感，导致算法聚类效果一般；DBSCAN算法聚类效果显著，本实验DBSCAN聚类效果好。

4．参考文献

[1] 鸢尾花(iris)数据集
DBSCAN聚类算法

机器学习--聚类系列--DBSCAN算法

java 实现DBScan聚类算法

初探DBSCAN聚类算法

DBSCAN算法

DBSCAN密度聚类算法（理论+图解+python代码）