使用回溯法解决编辑距离问题(C语言)

Posted 2022-12-04 Melody袁

回溯法

应用回溯法时，解空间往往以树的结构表示。回溯法以深度优先的方式搜索解空间树。如果回溯法在执行过程中判断解空间树的某个节点不包含问题的解时，则跳过对以该节点为根的子树的搜索，逐层向其祖先节点回溯；否则进入该子树，继续按深度优先策略搜索。
回溯法的搜索过程如下：从开始结点（根结点）出发，以深度优先的方式搜索整个解空间。这个开始结点就成为一个活结点，同时也成为当前的扩展结点。在当前的扩展结点处，搜索向纵深方向移至一个新结点。这个新结点就成为一个新的活结点，并成为当前扩展结点。如果在当前的扩展结点处不能再向纵深方向移动，则当前扩展结点就成为死结点。

此时，应往回移动（回溯）至最近的一个活结点处，并使这个活结点成为当前的扩展结点。回溯法即以这种工作方式递归地在解空间中搜索，直至找到所要求的解或解空间中已没有活结点时为止。简单来讲回溯法的基本思想就是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。

编辑距离

两个字符串之间，由一个转成另一个所需的最少编辑操作次数，设A和B是两个字符串，允许的字符操作包括：
(1)添加一个字符
(2)删除一个字符
(3)修改一个字符
要用最少的字符操作将字符串A转换为字符串B。
编辑距离d(A,B)的定义是把一个字符串A通过“插入、删除和替换”这样的编辑操作编程另外一个字符串操作变成另外一个字符串(B）所需要的最少编辑次数（代价或者费用最低)。从另外一个角度来看，可以将“字符串之间的编辑距离”视为“字符串之间的相似度”(和“最长公共子序列”问题有相同的视角)，也即“编辑距离”是将一个字符串转换成另外一个字符串的代价(转换的方法可能不唯一)，转换的代价越高则说明两个字符串的编辑距离越大，从而其相似度越低。
操作变成另外一个字符串(B)所需要的最少编辑次数(代价或者费用最低)。从另外一个角度来看，可以将“字符串之间的编辑距离”视为“字符串之间的相似度”(和“最长公共子序列”问题有相同的视角)，也即“编辑距离”是将一个字符串转换成另外一个字符串的代价(转换的方法可能不唯一)，转换的代价越高则说明两个字符串的编辑距离越大，从而其相似度越低.

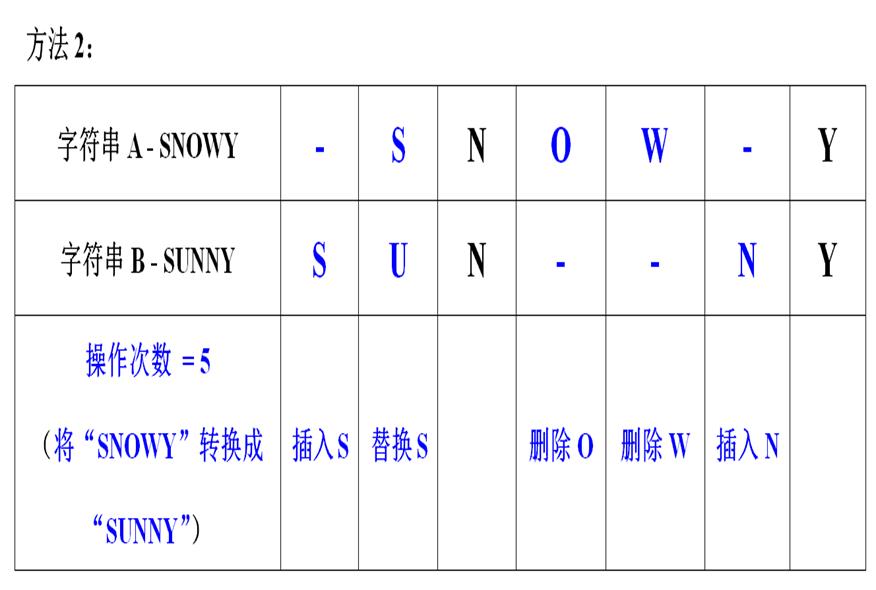
可以判定，字符串 SNOWY 和 SUNNY 之间的编辑距离为 3。

解：
编辑距离问题的最优子结构性质
编辑距离问题需要多个步骤处理。对字符串 A 做最少修改步骤变换到字符串 B，每个步骤都不是独立的，受前面已经确定的步骤和后面可选步骤的共同影响。设字符串 A 有 m 个字符，字符串 B 有 n 个字符。假定已经得到将 A 的 1 ~ m 个字符转换为 B 的 1 ~ n 个字符所需要的最优解，即最少编辑次数；那么其子问题“将 A 的 1 ~ i 个字符转换为 B 的 1 ~ j 个字符”也一定是最优的，否则的话（反证法），存在一个子问题的最优解，从而导致整个问题有一个更少的编辑次数，这和已知的最优解矛盾。所以编辑距离存在最优子结构性质。

建立状态方程

代码

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <iostream>

using namespace std;


#define STR_LEN           100
#define TRUE              1
#define FALSE             0


int  FindTripleMin( int a, int b, int c );
int  CalcEditDistance( char *StrA, char *StrB, int **d );
void PrintEditDistanceMatrix( int **d, int RowNum, int ColNum );

char StrA[ STR_LEN ];
char StrB[ STR_LEN ];
int  d[STR_LEN][STR_LEN];
int pp[STR_LEN][STR_LEN];


int FindTripleMin( int a, int b, int c )

    int t = ( a < b ) ? a : b;

    return ( ( t < c ) ? t : c );



// ( 1 ) A = fxpimu  B = xwrs  d( A, B ) = 5
// ( 2 ) A = abc     B = cba   d( A, B ) = 2
// ( 3 ) A = stot    B = stop  d( A, B ) = 1
// ( 4 ) A = cd      B = abcb  d( A, B ) = 3
int CalcEditDistance()

    
    for( int i = 0; i <= strlen( StrA ); i++ )
        d[ i ][ 0 ] = i;

    for( int j = 0; j <= strlen( StrB ); j++ )
        d[ 0 ][ j ] = j;

    
    for( int i = 1; i <= strlen( StrA ); i++ )
        for( int j = 1; j <= strlen( StrB ) ; j++)
            char x = StrA[i-1];
            char y = StrB[j-1];
          
            if(x == y)
                d[i][j] =d[i-1][j-1] + 0;
            
            else
                d[i][j] = FindTripleMin(d[i][j-1]+1 , d[i-1][j] + 1 , d[i-1][j-1] + 1);
            
        
    


    return d[ strlen( StrA ) ][ strlen( StrB ) ];


int FindBack()

    int m = strlen( StrA );
    int n = strlen( StrB );

    while (n>=0 || m>=0)
       
        if (n && d[m][n-1]+1 == d[m][n])
        
            //printf("%d " ,m);
            printf("\\t插入 %c\\n" , (StrB[n-1]));
            n -= 1;
            continue;
        
        
        if (m && d[m-1][n]+1 == d[m][n])
        
            //printf("%d " ,m);
            printf("\\t删除 %c\\n" , (StrA[m-1]));
            m -= 1;
            continue;
        
        
        if (d[m-1][n-1]+1 == d[m][n])
        
            //printf("%d " ,m);
            printf("\\t替换 %c ---  %c\\n" , StrA[m-1],StrB[n-1]);
            n -= 1;
            m -= 1;
            continue;
        
        if (d[m-1][n-1] == d[m][n])
        
            n -= 1;
            m -= 1;
        
    



void PrintEditDistanceMatrix(int RowNum, int ColNum )

    int i, j;

    printf( "\\t编辑距离矩阵是 : \\n" );
    for ( i = 0; i <= RowNum - 1; i++ )
    
        printf( "\\t" );
        for ( j = 0; j <= ColNum - 1; j++ )
            printf( "%d ", d[ i ][ j ] );
        printf( "\\n" );
    
    printf( "\\n\\n" );



int main(void)


    int  i, m, n, dAB;

    system( "cls" );

    printf( "\\n\\n\\t输入字符串A  : " );
    //cin >> StrA ;
    scanf( "%s", StrA );
    m = strlen( StrA );

    printf( "\\n\\t输入字符串B: : " );
    getchar();
    //cin >> StrB ;
    scanf( "%s", StrB );
    n = strlen( StrB );


  
    dAB = CalcEditDistance();
    FindBack();
    
    cout << "\\t编辑距离: " << dAB <<endl;
    

    PrintEditDistanceMatrix(( m + 1 ), ( n + 1 ) );

    for ( i = 0; i <= m; i++ )
        free( d[ i ] );
    free( d );
    return 0;



//