运筹学-动态规划实例

Posted 2022-12-03 书槑

动态规划是解决多阶段决策问题最优化的一种方法，目标是达到整个过程的整体最优。一种解法是从最后一阶段开始，用逆序递推方法求解。

三个小例子

• 分配医疗队
• 雇佣工人
• 工厂生产

分配医疗队

世界卫生组织要求将五支医疗队分配到三个国家，分配的医疗队的数目对各国家的效益如表11.1所示。（注：效益指延长该国家人的寿命）

设：
$s_i$为状态变量，即能够分配给第i个国家（以及剩下的国家）的医疗队数目
$x_i$为决策变量，即实际分配给第i个国家的医疗队数目
$x_i^{\star }$为最优的xi
$f_n(s_n,x_n^{\star })$为最优指标函数，即第n个阶段的最大效益
$f_i^{\star }(s_i)=f_n(s_n,x_n^{\star })$
因此

我们从最后一个阶段（即第三个国家）开始，用列表法求解

接着是上一个阶段（即第二个国家）
以$s_2=2$为例解释一下这张表
$s_2=2$表示还剩两支医疗队能分配给第二、三个国家，因此能给第二个国家分配的医疗队数目为0，1，2.分配效益即为第二个国家和第三个国家的效益之和。$f_2^{\star }(s_2)$取每行中的最大值，$x_i^{\star }$为相应的$x_2$的取值。

最后是第一阶段（即第一个国家）
同理可以求出第一阶段最优的决策变量

可以看出，最优的决策方案是给第一个国家分配1支医疗队，这时$s_2=4$，则应该给第二个国家分配3支医疗队，因此最后给第三个国家分配1支医疗队

雇佣工人

某工厂在一年四季对工人的需求量不同，下表中展示了每季对工人的最低需求，若实际雇佣人数多于最低需求则要为多雇的工人支付2000美元工资。换季时每次雇佣或解雇工人均需支付(200*变动人数${}^2$)元的手续费。

这个问题可以看作是四阶段的动态规划问题。
决策变量$x_n$表示该阶段需要雇佣的人数
状态变量$s_n$表示上一阶段的雇佣人数，即$s_n=x_{n-1}$
$r_n$表示每季对工人的最低需求
生产从春季开始，因此春季雇佣的人数是确定的255人，即$x_4^{\star }=255$，而由于由于这四个季节是一个循环，且最后一阶段的最优值必须是已知的或者不依赖于其他阶段，因此我们将春季作为最后一个阶段。可以列出春季的决策表：

其中的$s_4$为冬季的雇佣人数，需满足最低需求且没必要大于各季最低需求的上界。

接着可以列出上一个阶段（冬季）的决策表

其中

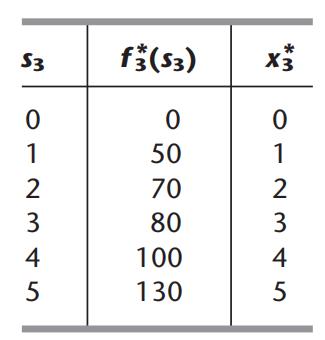
$s_3$可以看作已知，因此可以求出$x_3$最优值的表达式

解得

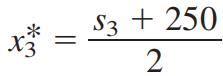
带入$f_3^{\star }(s_3)$中即可
注意，因为$x_3^{\star }$即为$s_4$,因此需要检查一下$x_3^{\star }$的范围，此处是符合要求的

进入上一个阶段（秋季）

同理，先写出$f_2^{\star }(s_2)$的表达式


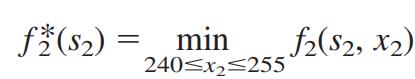
将$s_2$看作已知，求出$x_2$最优值的表达式

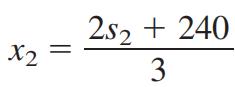
注意，此处$s_2$的范围是[220,255]，但$x_2$的范围应当是[240,255]，对应$s_2$的范围是[240,255]，因此对$s_2$分段，分别求出$x_2$最优值的表达式. 当$s_2$的范围是[220,240]时，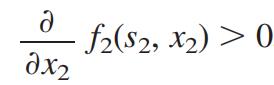
因此$x_2=240$ 时函数取最小值

最后是第一阶段（夏季）的决策表

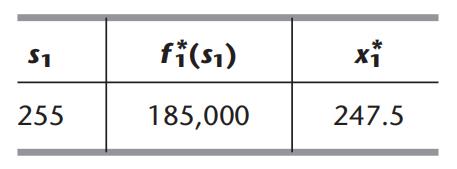
其中$s_1=255$是已知的春季雇佣人数
因为$x_1=s_2$是分段的，所以

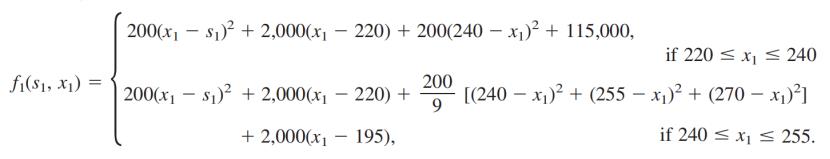
对每一段分别求出最小值，并进行比较
对 $220\le x_1\le 240$,

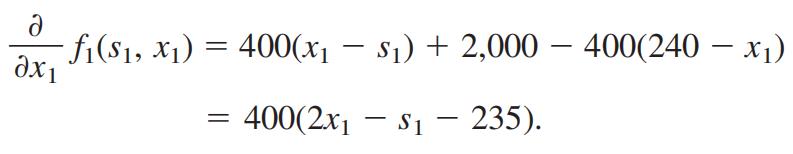
因此

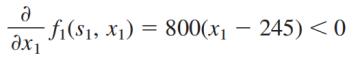
即$x_1=240$ 时取最小值

对 $240\le x_1\le 255$,

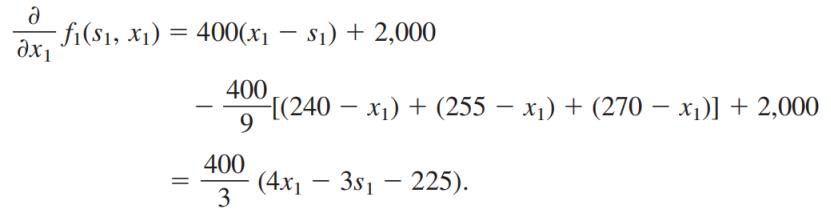
解得$x_1=247.5$

将两个$x_1$值分别带入比较，发现$x_1=247.5$时$f_1(s_1)$的值更小，是185,000

因此这个问题就解决了: x