数据结构与算法:树 2-3树,2-3-4树,B树 B+树 B*树 (了解)

Posted 2022-12-03 史大拿

Tips: 采用java语言,关注博主,底部附有完整代码

工具:IDEA

本系列介绍的是数据结构: 树

这是第十篇目前计划一共有11篇:

1. 二叉树入门
2. 顺序二叉树
3. 线索化二叉树
4. 堆排序
5. 赫夫曼树(一)
6. 赫夫曼树(二)
7. 赫夫曼树(三)
8. 二叉排序树(BST)
9. 平衡二叉排序树AVL
10. 2-3树,2-3-4树,B树 B+树 B*树 了解 本篇
11. 数据结构与算法:树 红黑树 (十一)

敬请期待吧~~

2-3树

基本了解

2-3树是一个可以有2个子结点或者3个子结点的树.

• 当一棵树当前结点为1个结点,并且 2个子结点又叫2叉树

• 当一棵树当前结点为2个结点 并且 3个子结点又叫3叉树

2-3树必须符合是一颗完美AVL树的所有特性!

特别注意: 2-3树结点是从叶子结点到根结点通过 拆分 合并 往上长

而不是从根结点到叶子结点往下长! (后面会介绍)

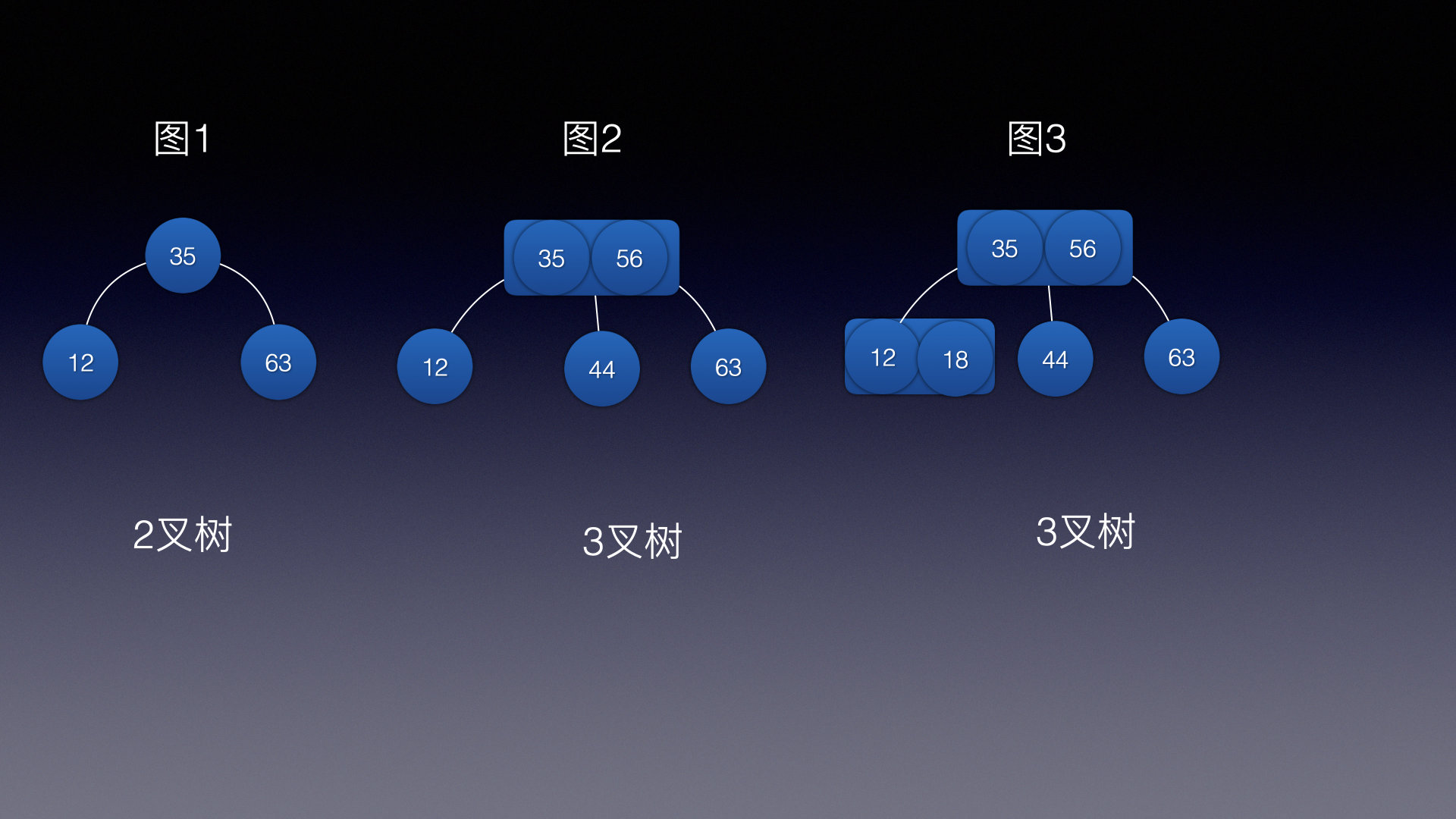
特性:

• 2结点的特性满足完美AVL树,左子结点 < 当前结点 < 右子结点

• 3结点特性: 左子结点 < 当前结点 < 中子结点 < 右子结点

如果左子 / 右子结点有2个结点,那么就从往右排列

例如图3:

左1结点 < 左2结点 < 当前1结点 < 当前2结点 < 中子结点 < 右子结点

12 < 18 < 35 < 44 < 56 < 63

再来看一组反面教材

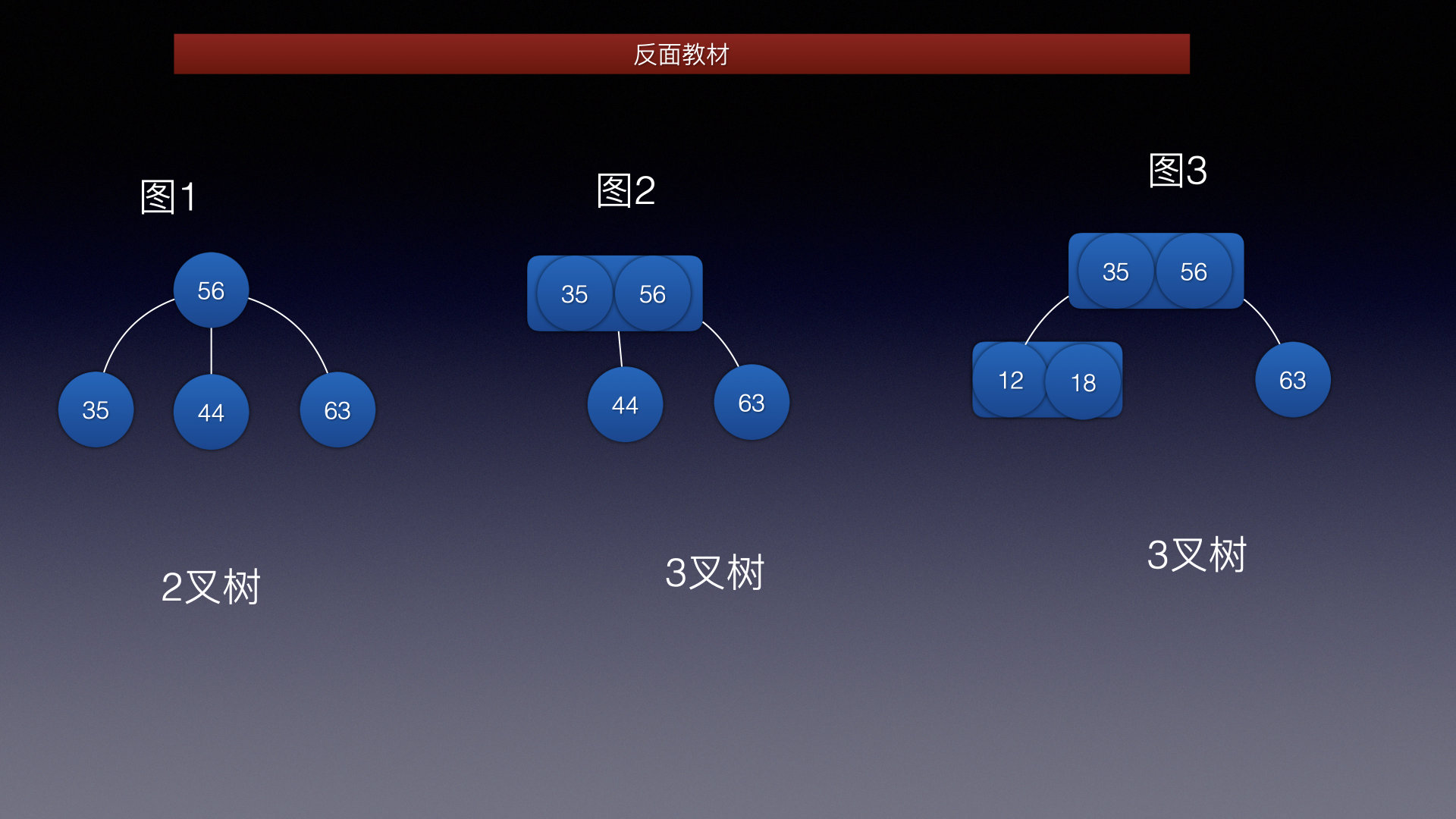
• 图1: 父结点有1个,子结点有2个不满足
• 图2,图3: 父结点有2个,子结点有2个不满足

拆分与合并

拆分

3结点拆分成2结点:

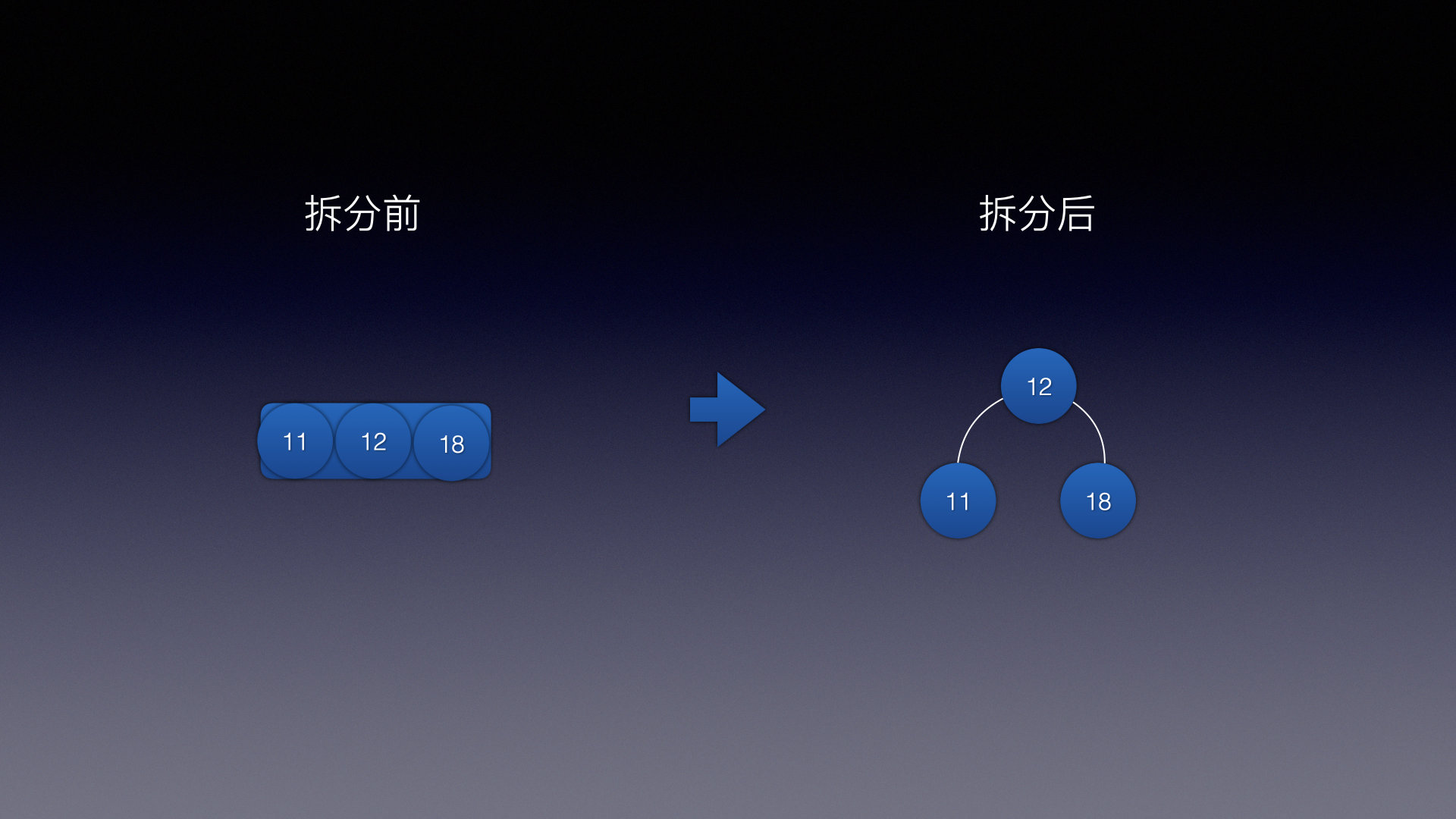
• 中子结点变成父结点

• 原本左子结点变成中子结点的左子结点

• 原本右子结点变成中子结点的右子结点

合并

合并的逻辑和2叉树添加一个结点有所不同

• 2叉树,左子 / 右子结点 为null就插入,因为他的父结点只有1个
• 2-3树则优先考虑父结点是2个的情况,优先构建3叉树!

插入结点

插入结点其实就是拆分与合并的体现

来看看完整流程:

提取出每个插入结点关键帧看一看:

插入结点1:

插入结点2:

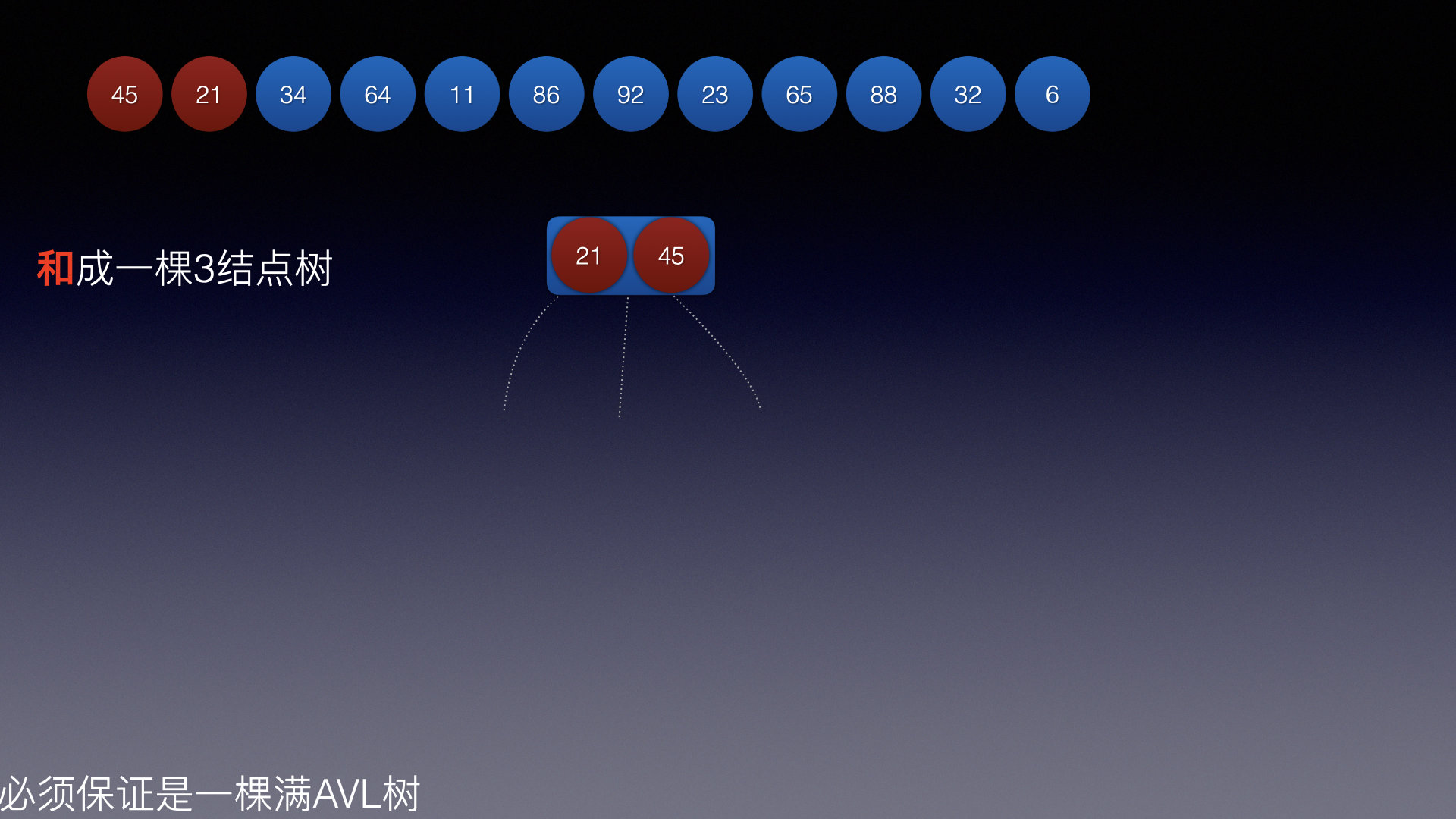
插入结点3:

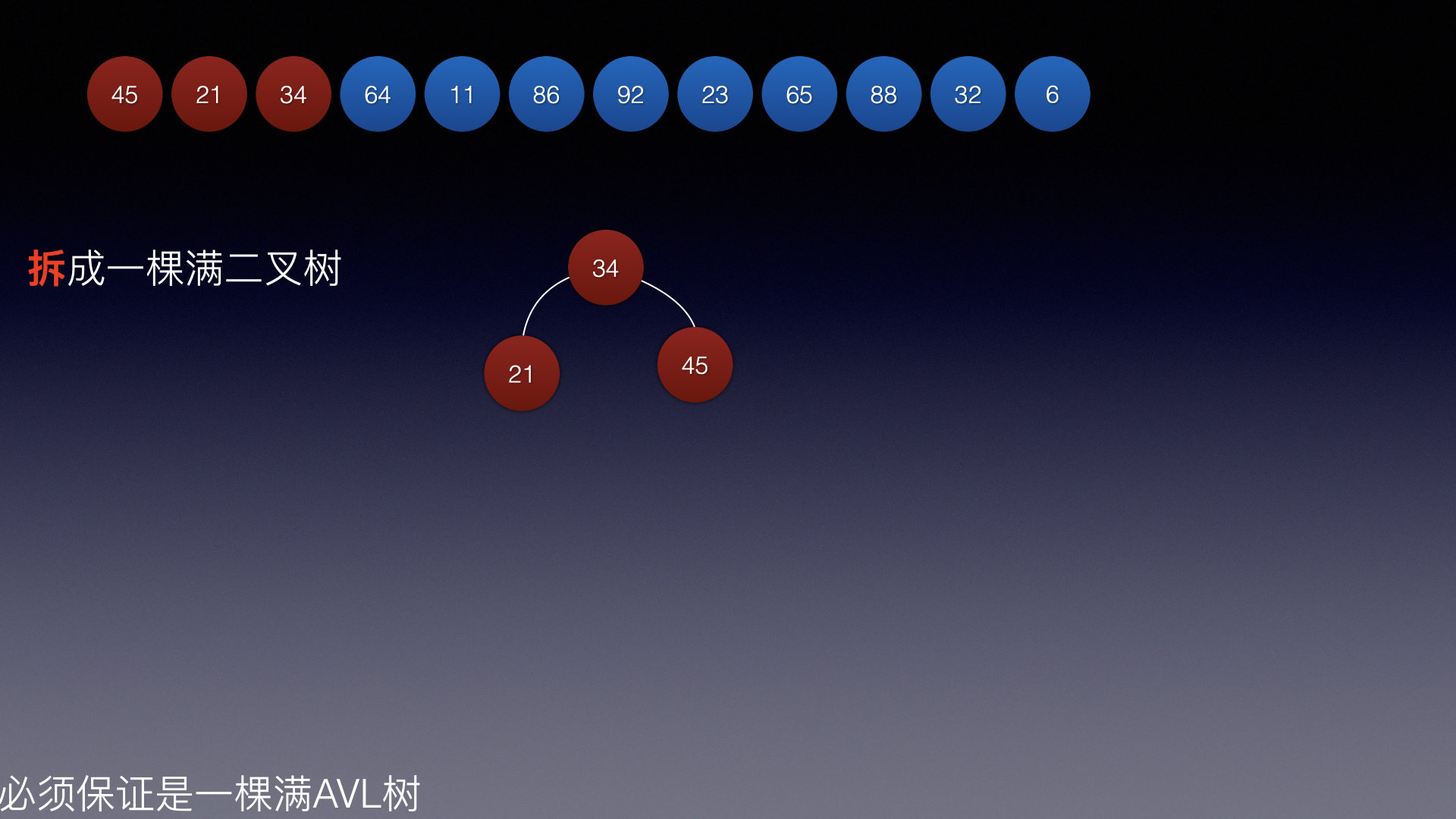
插入结点4:

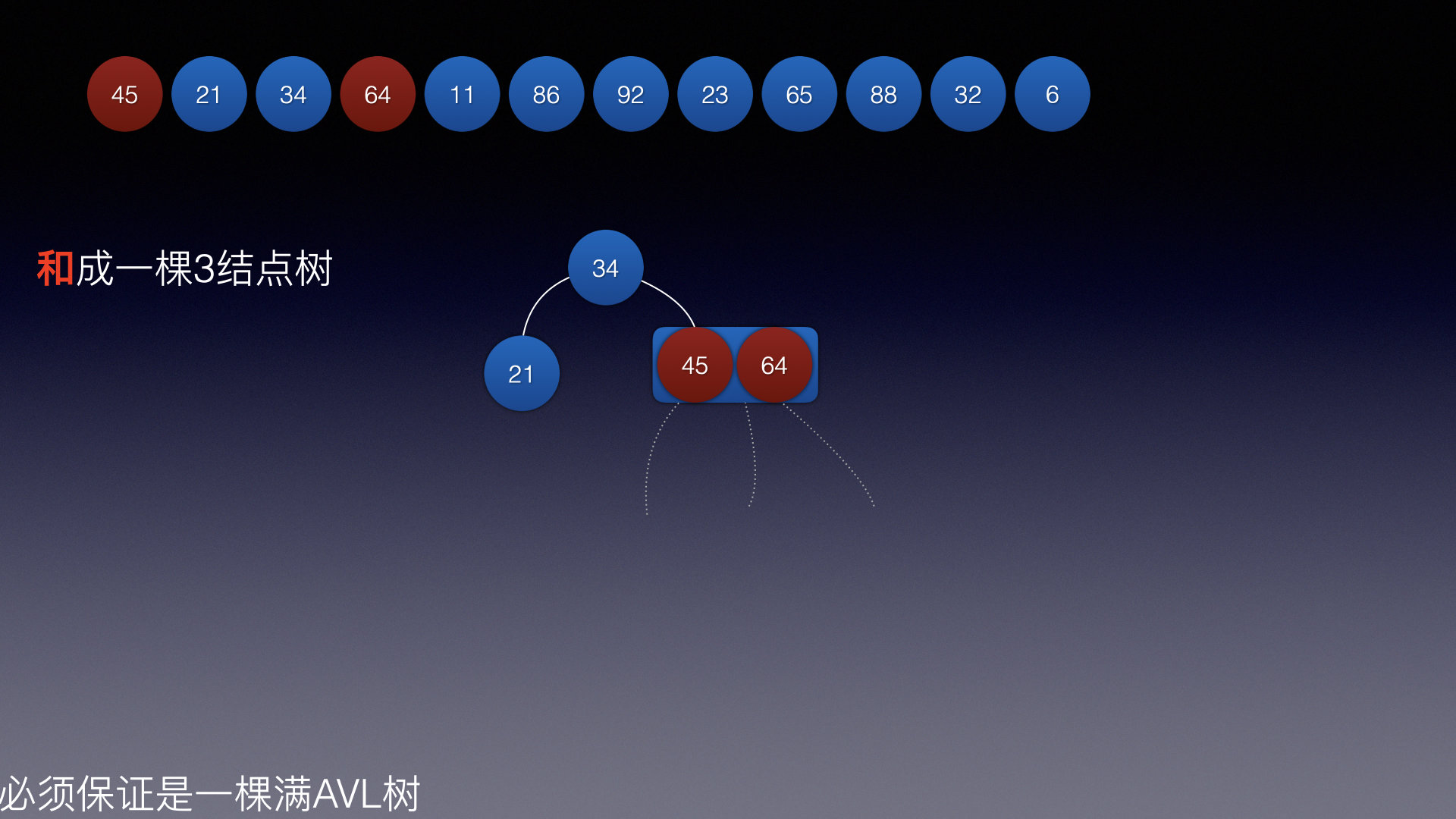
插入结点5:

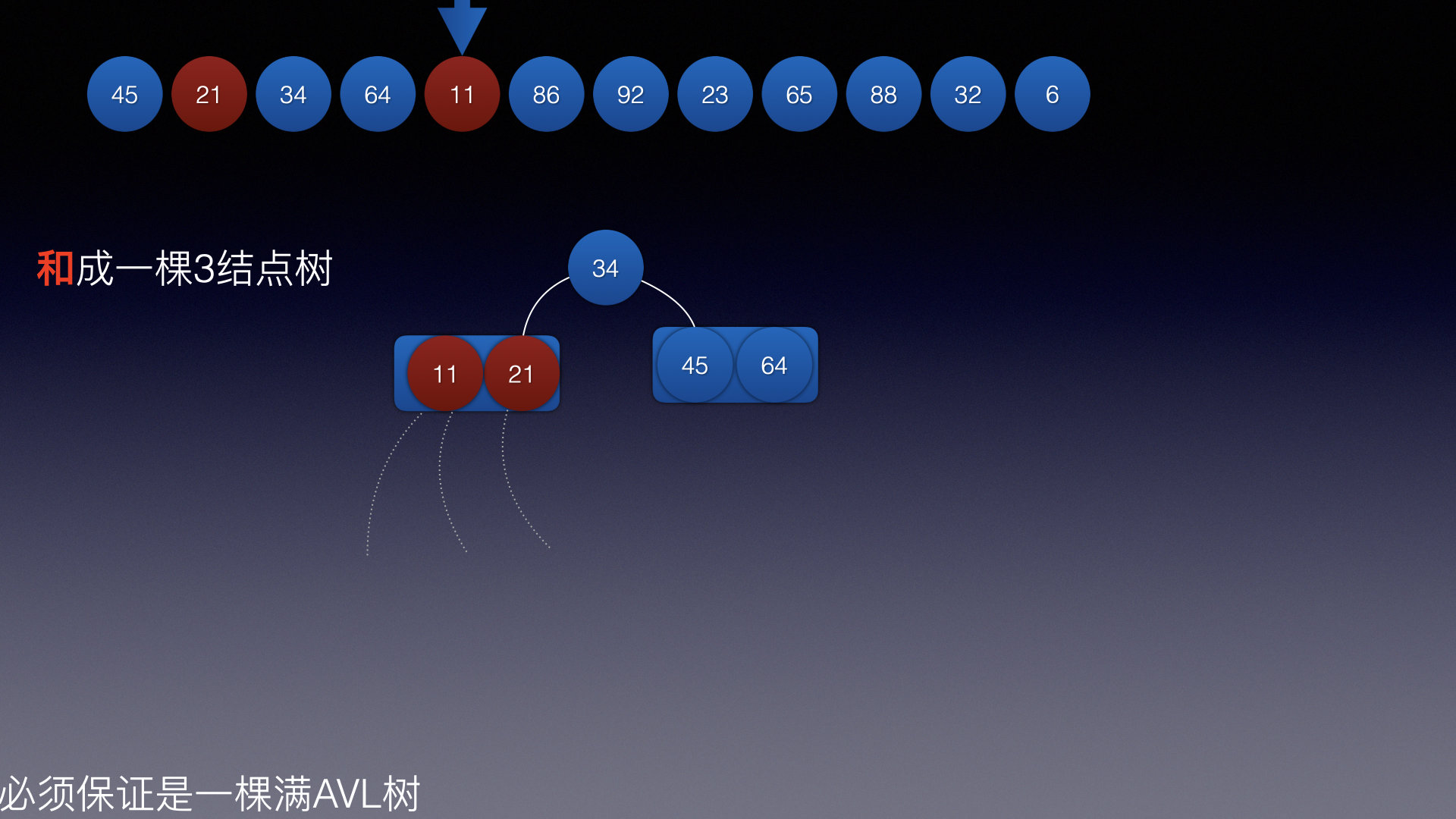
插入结点6:

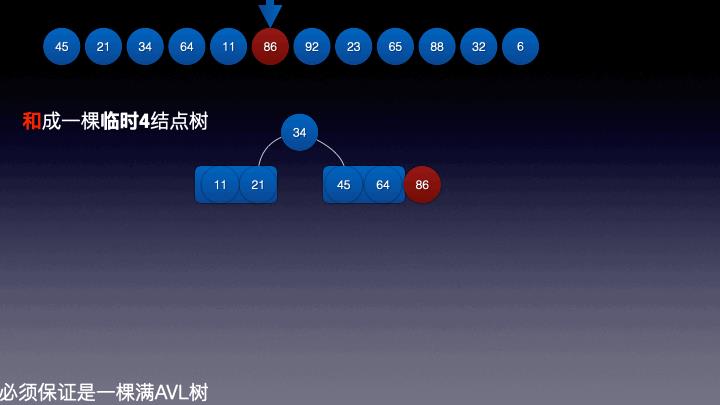
插入结点7:

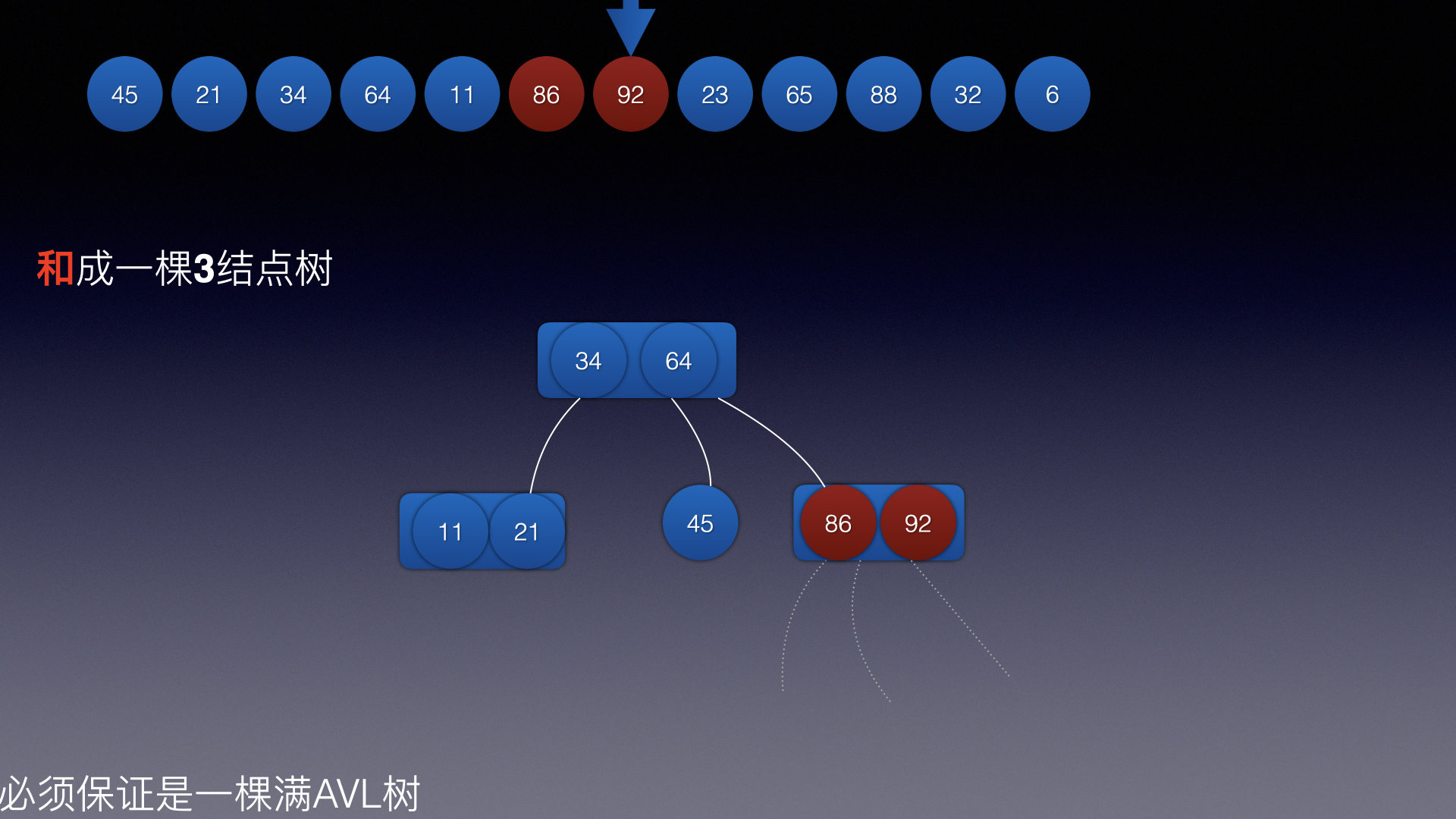
插入结点8:

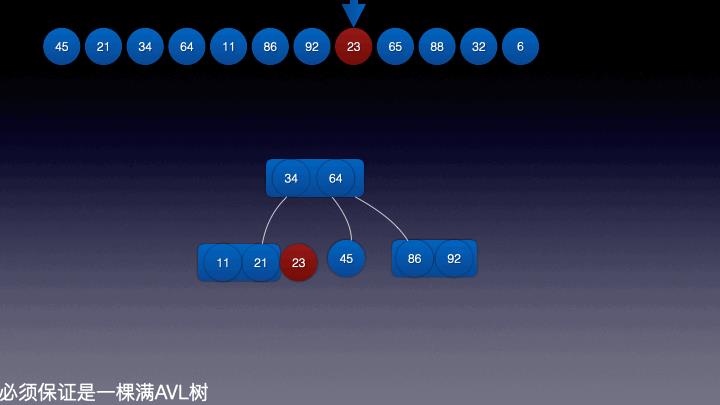
插入结点9:

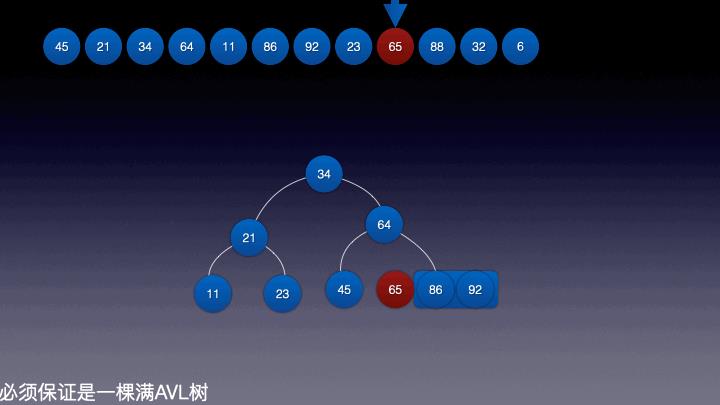
插入结点10:

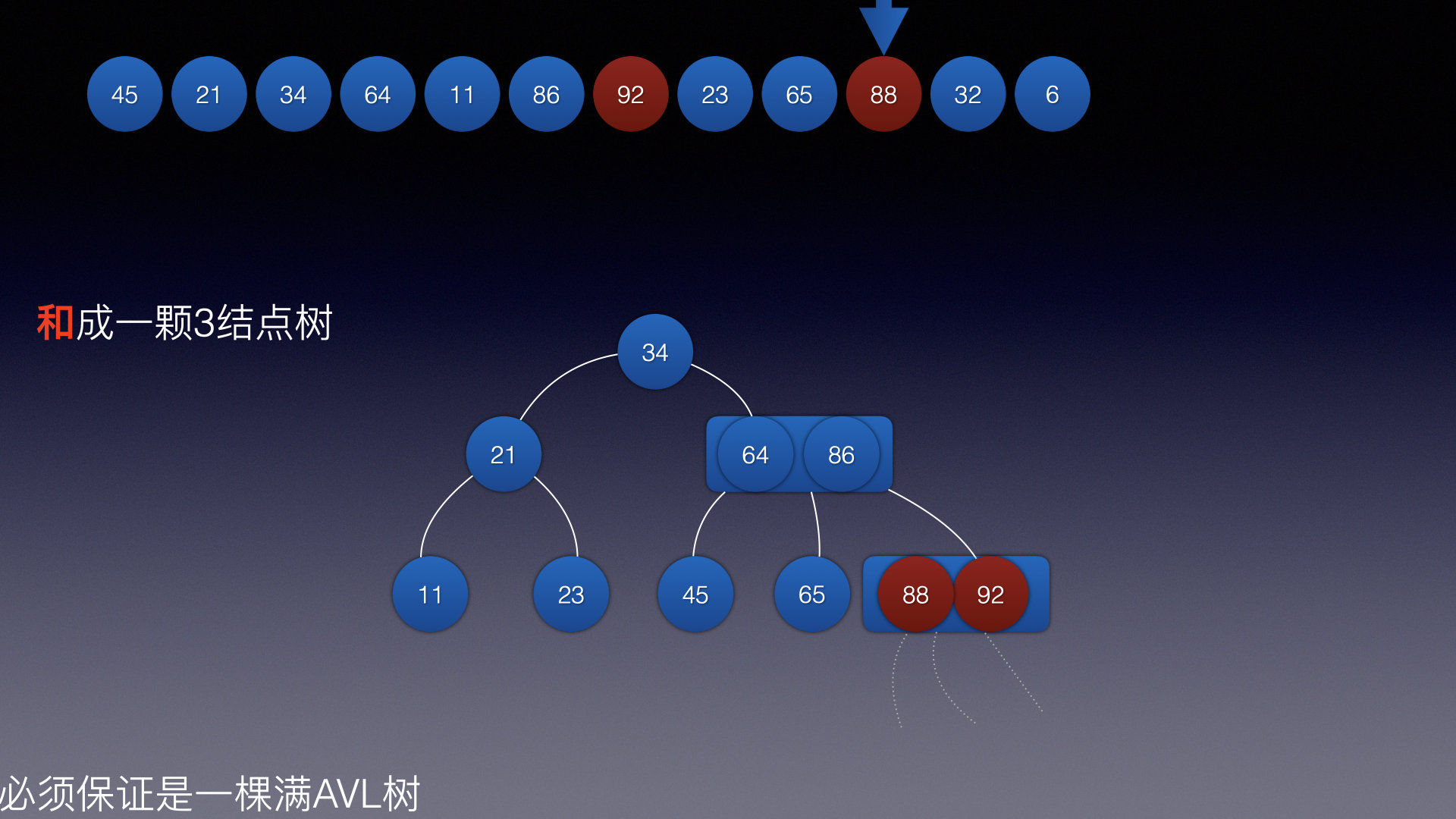
插入结点11:

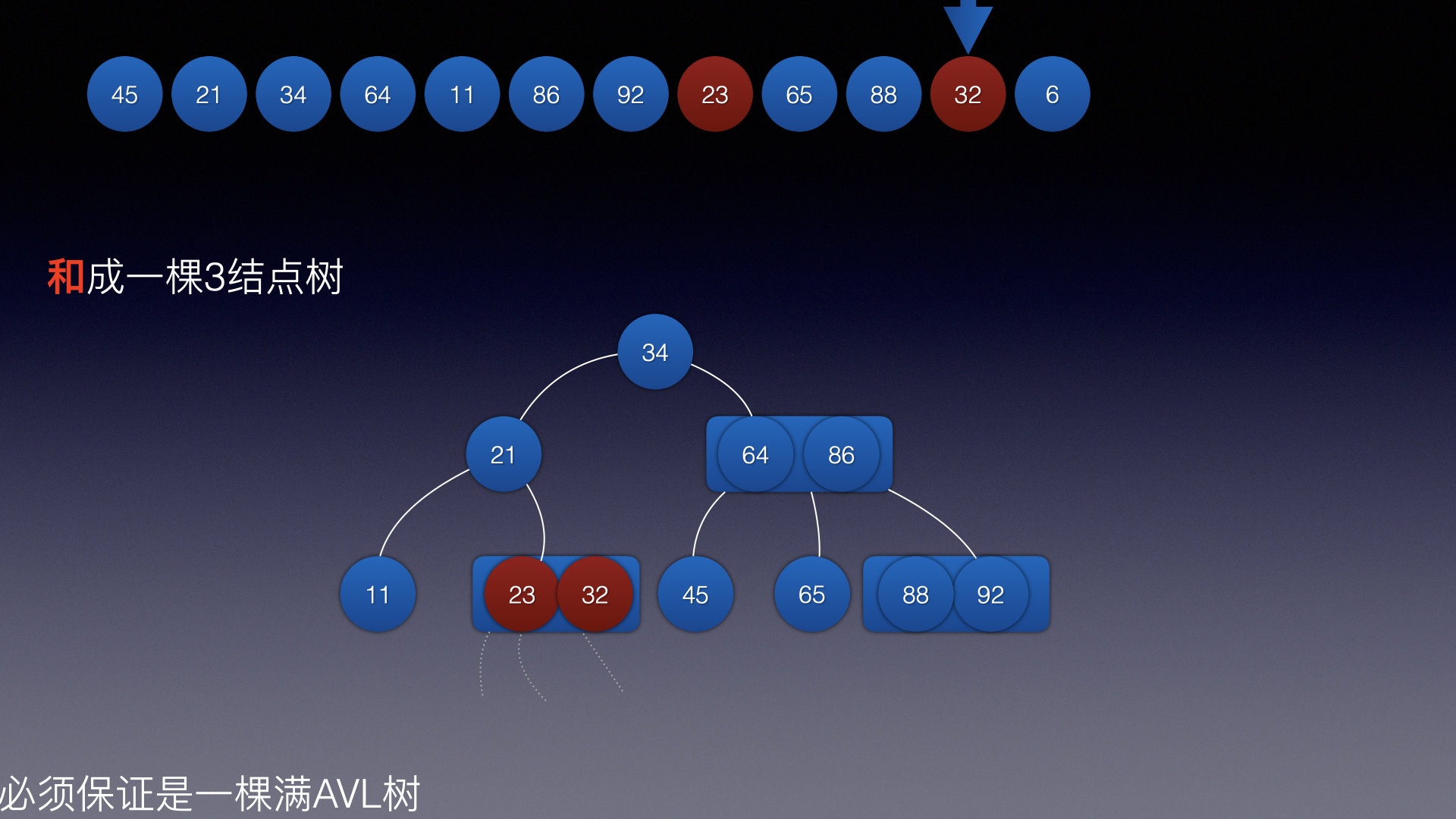
插入结点12:

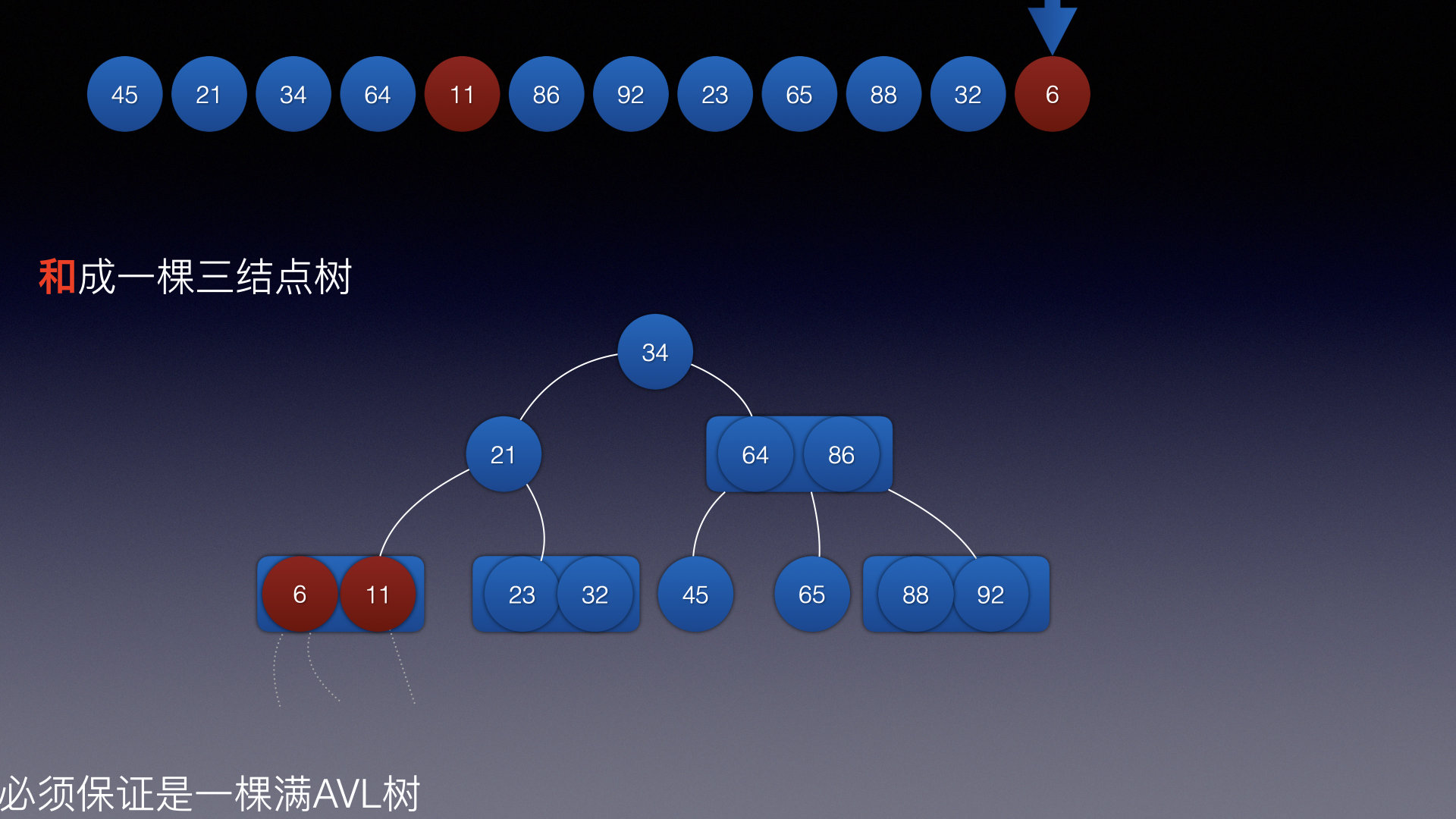
希望插入流程对你有所帮助!

删除结点

情况1:

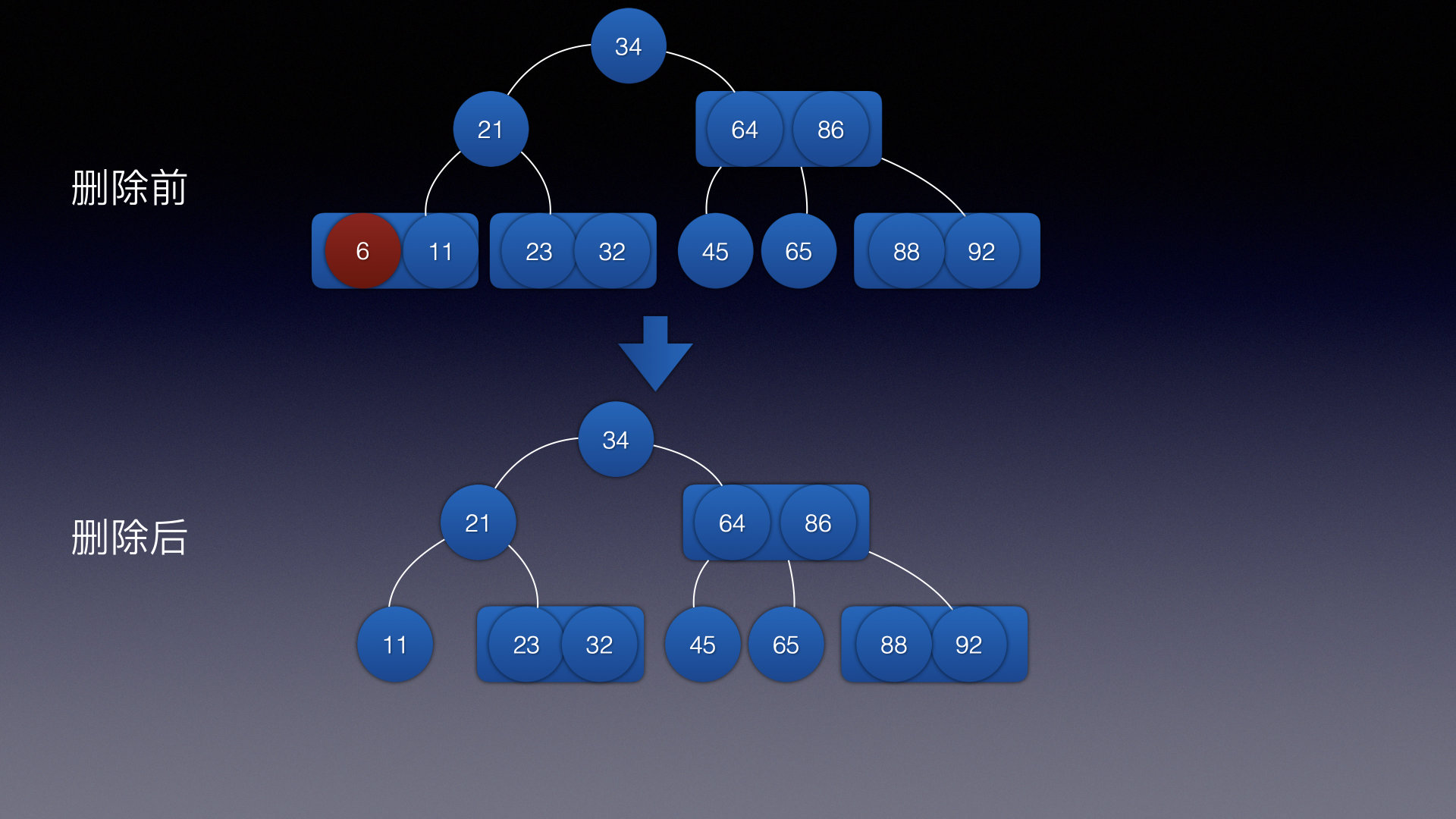
情况2:

因为删除的结点只有1个结点,删除后就不满足完美树的特性了,所以需要先左旋保证删除后保证完美性!

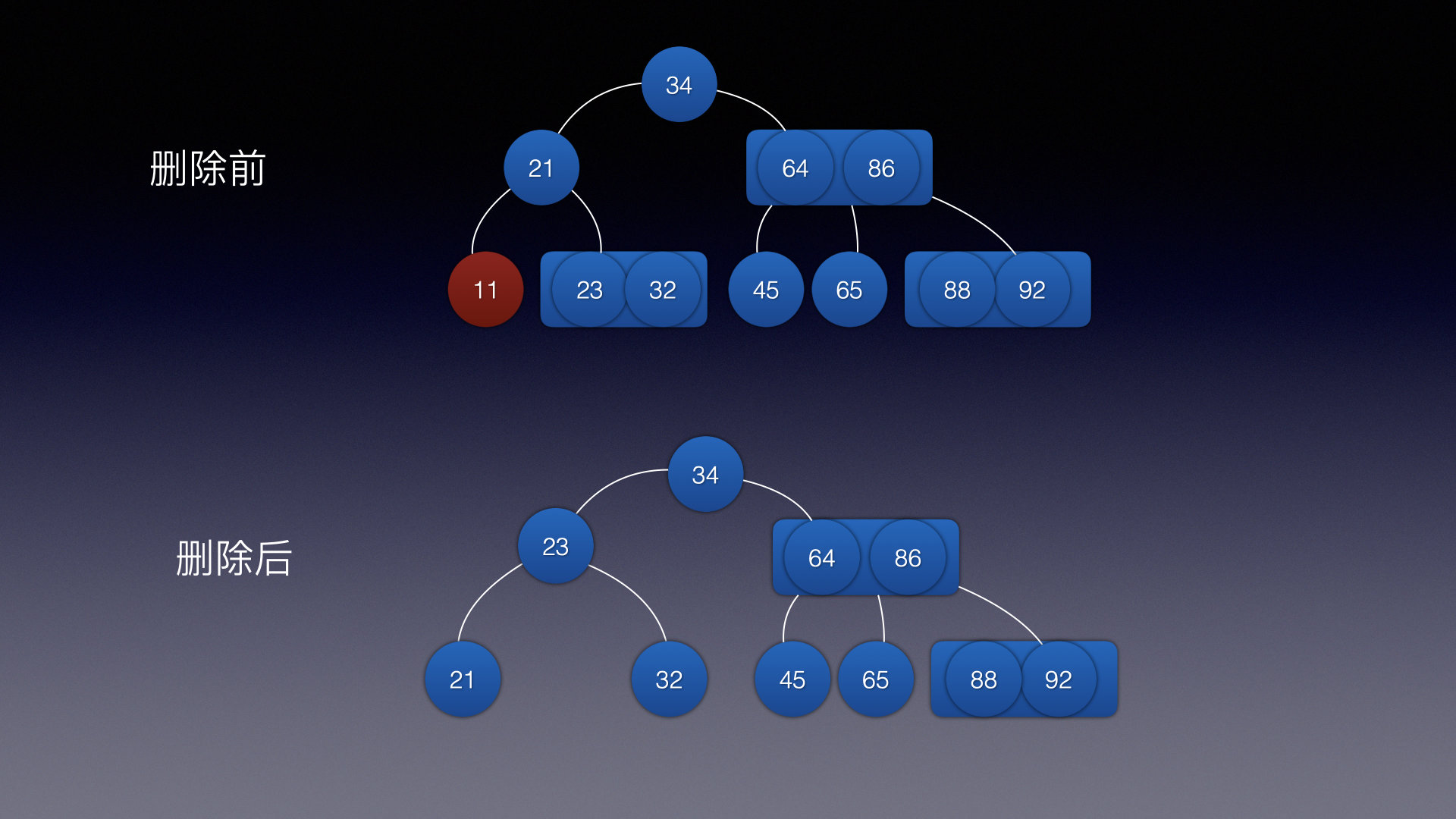
情况3:

这里左旋应该不太好理解

可以理解为: 用后继结点代替当前结点位置,直到要删除的结点为3叉树

其实感觉左旋说起来不太标准,但是我搜了一圈,国内国外的都看了,全是说的左旋…

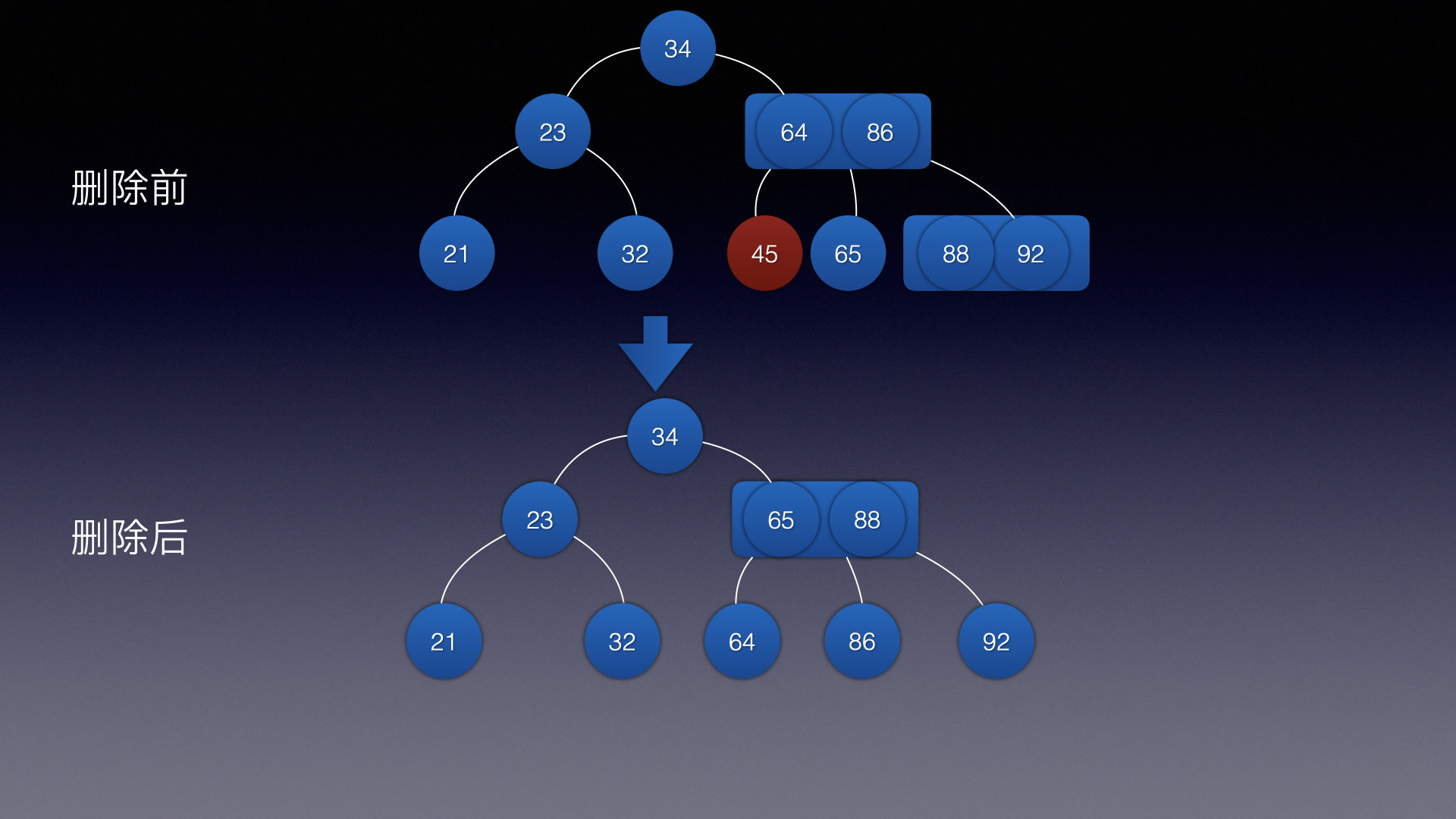
情况4:

还是通过左旋,将2叉树转变为3叉树,然后删除

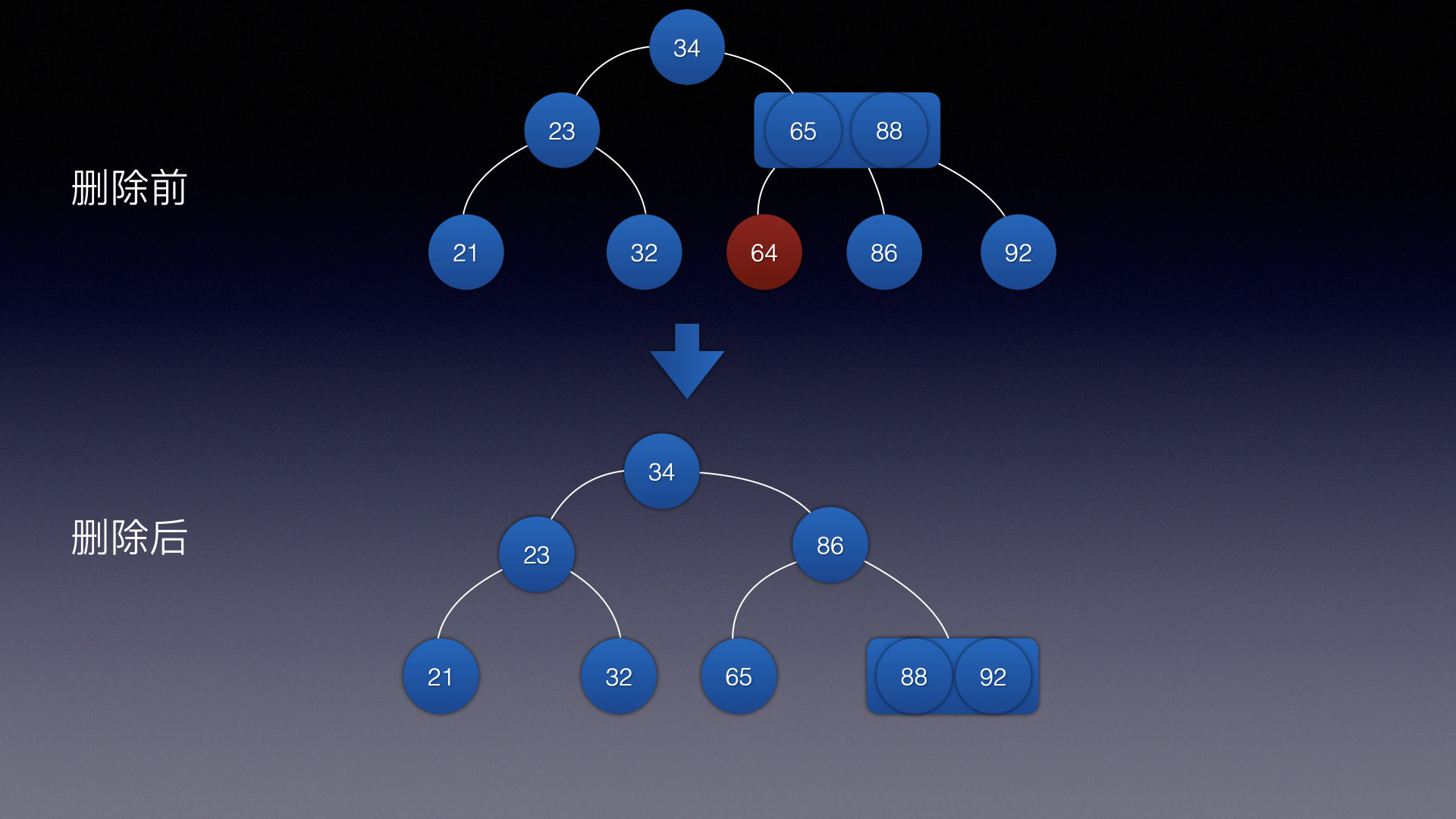
情况5:

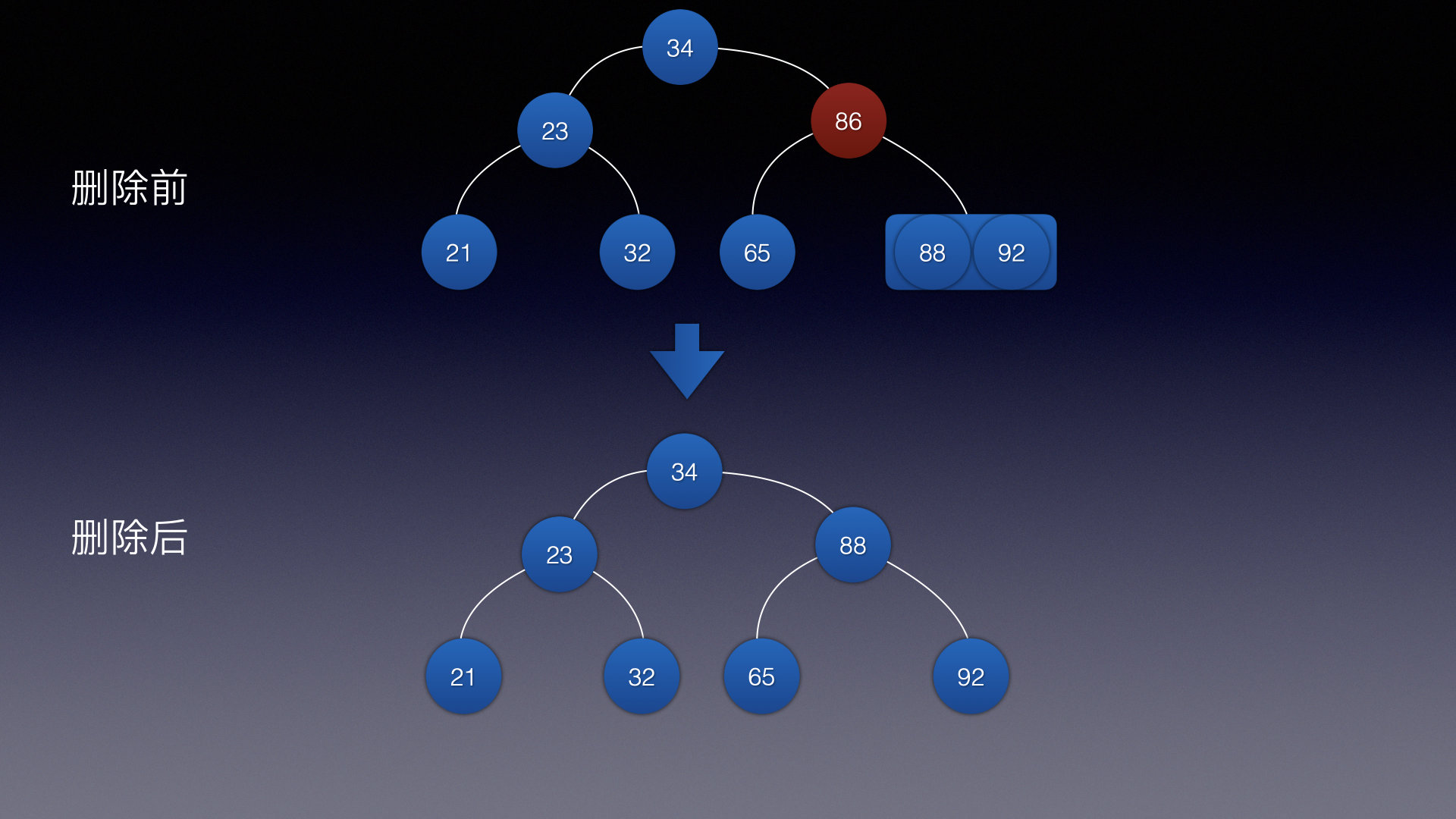
情况6:

这种如果是一棵完美AVL树的话就不能旋转了,因为在怎么旋转删除后还是不完美的

需要先删除后,在想办法拆分合并成新的完美树

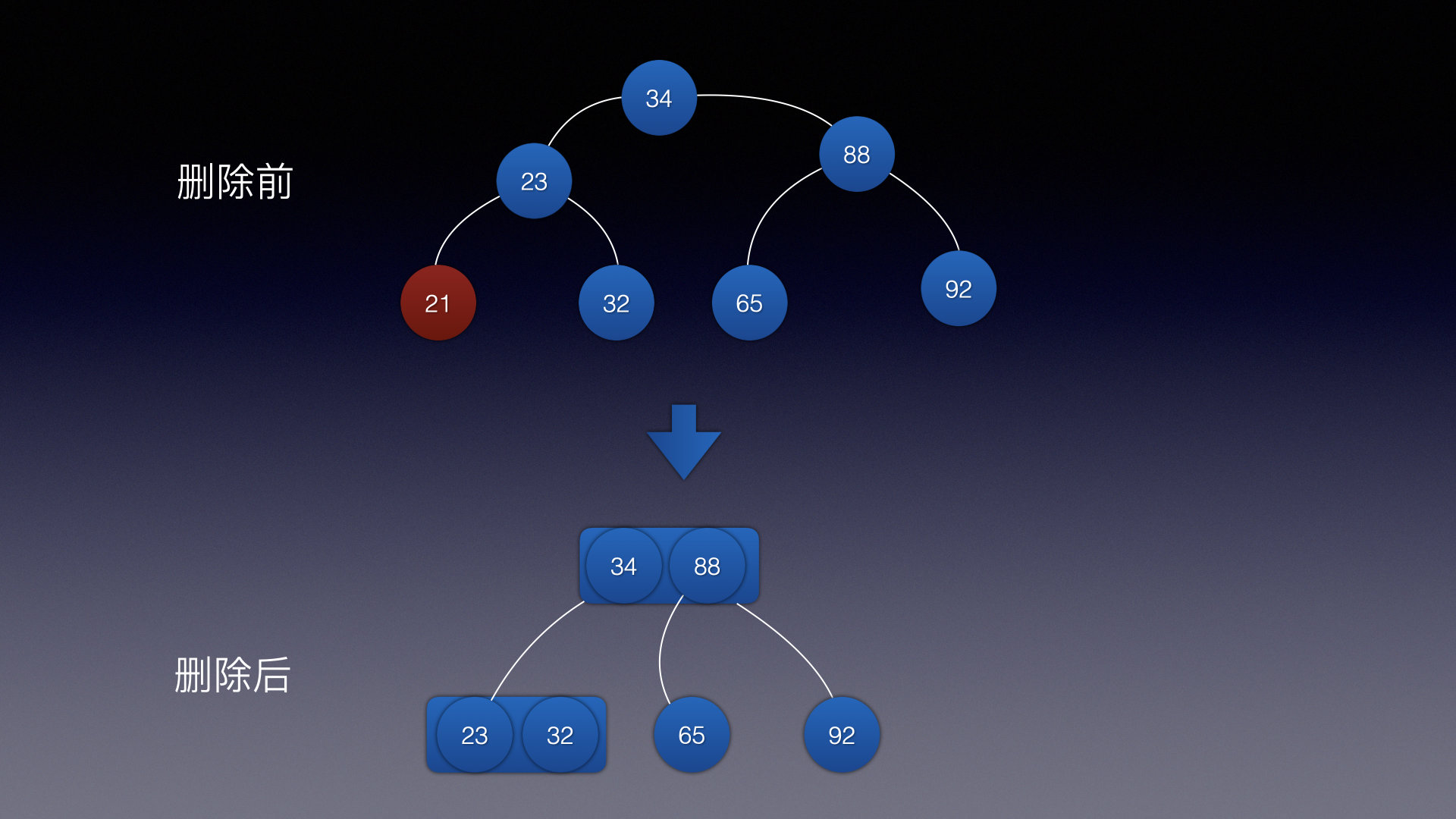
应该还有其他情况,毕竟本篇只是当作了解,主要的插入结点和下面提到的 和红黑树的关系搞懂就可以!

2-3树和红黑树的映射

Tips: 看不懂或者不知道红黑树的也没关系, 只需要知道红黑树是一个红结点或者一个黑结点构成的树即可,下2篇会详细讲到,这里看懂这些代码即可!!!

流程:

• 2结点成为一个新的黑色节点。

• 将3结点分为两个2结点，并在它们之间插入一个链接。我们沿着左节点向下移动，使链接向左倾斜。

• 左侧结点点（向下移动）成为新的红色节点，右侧节点成为新的黑色节点。

看不懂没关系,又分析出几张图:

情况1:

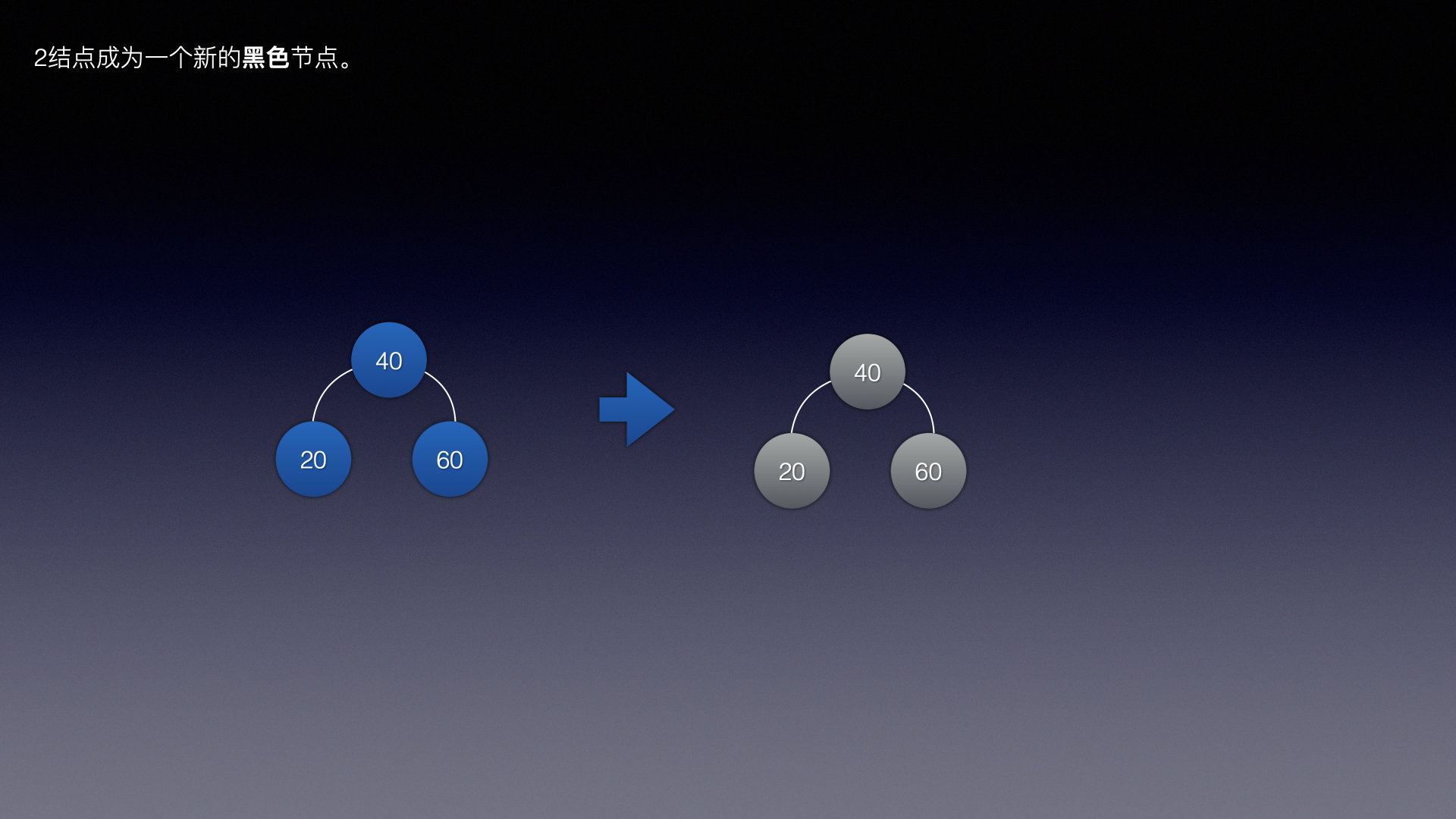
如果是2叉树,并且结点都有1个结点,则都变成黑色结点

情况2:

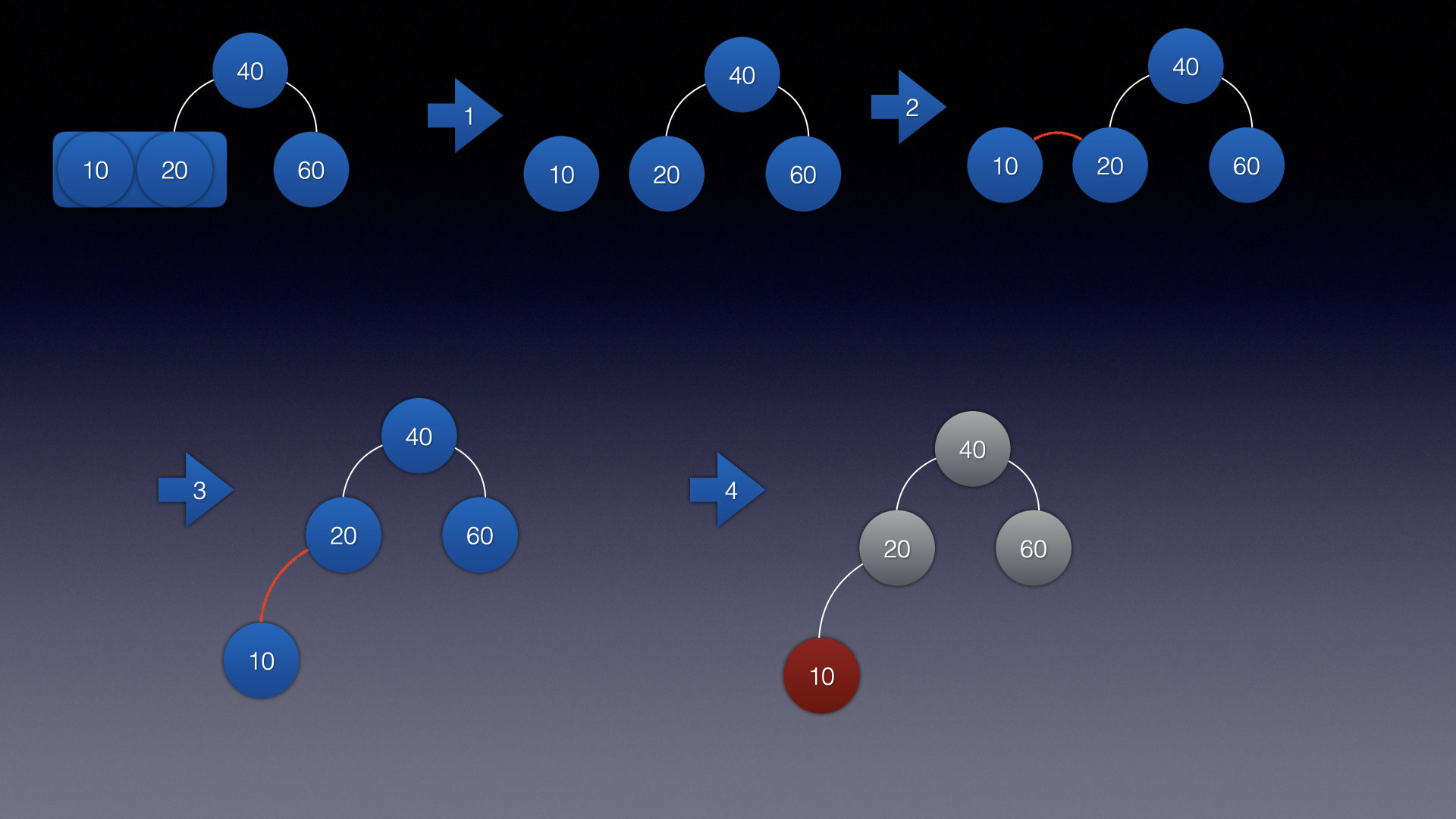
如果是2叉树, 并且左子结点包含2个结点,

让这2个结点拆分成2个结点

• 第一个结点:10
• 第二个结点:20

并且让第1个结点变成红色,第二个结点变成黑色即可

情况3:

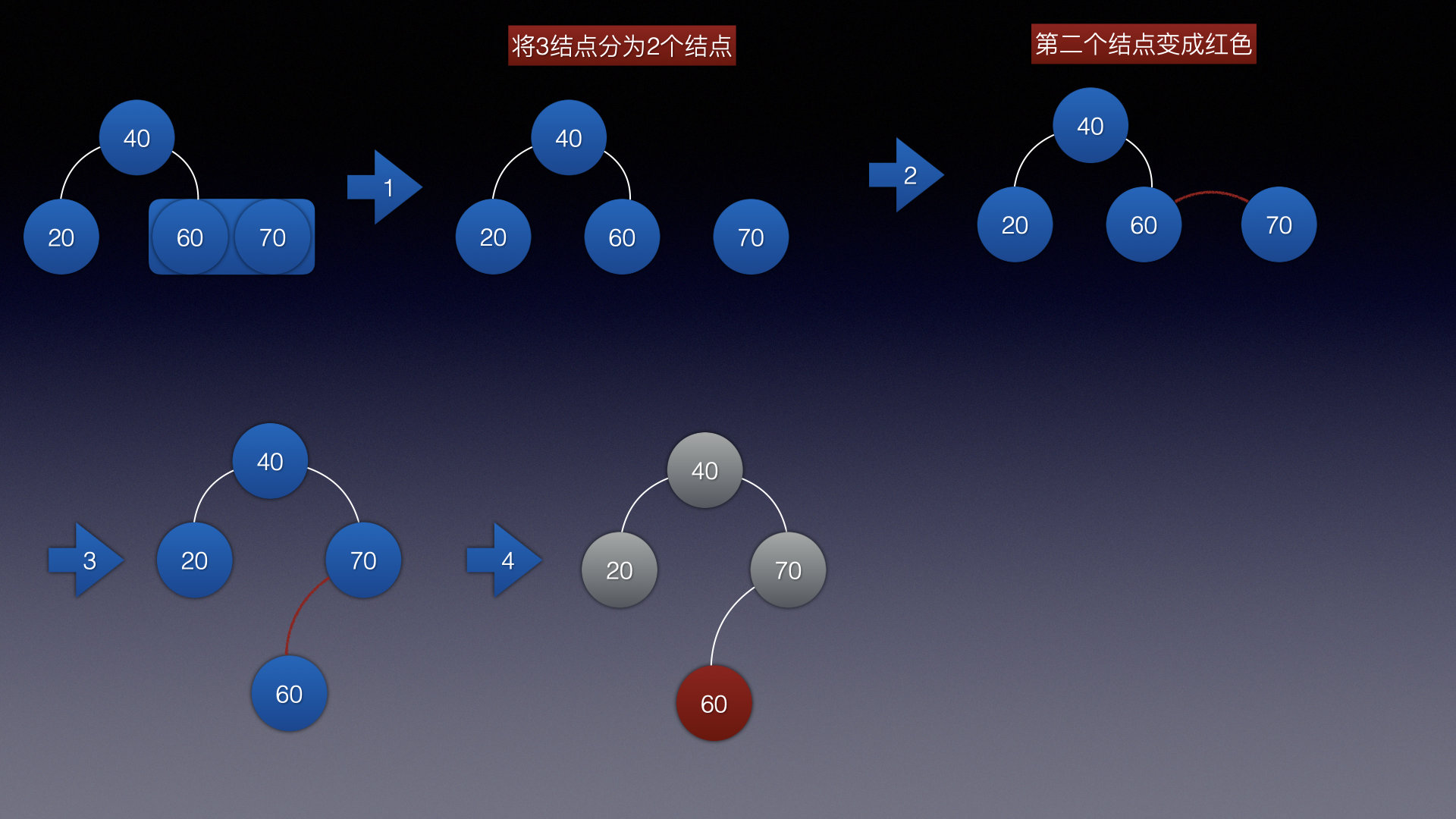
情况3和情况2道理相同,不解释

情况4:

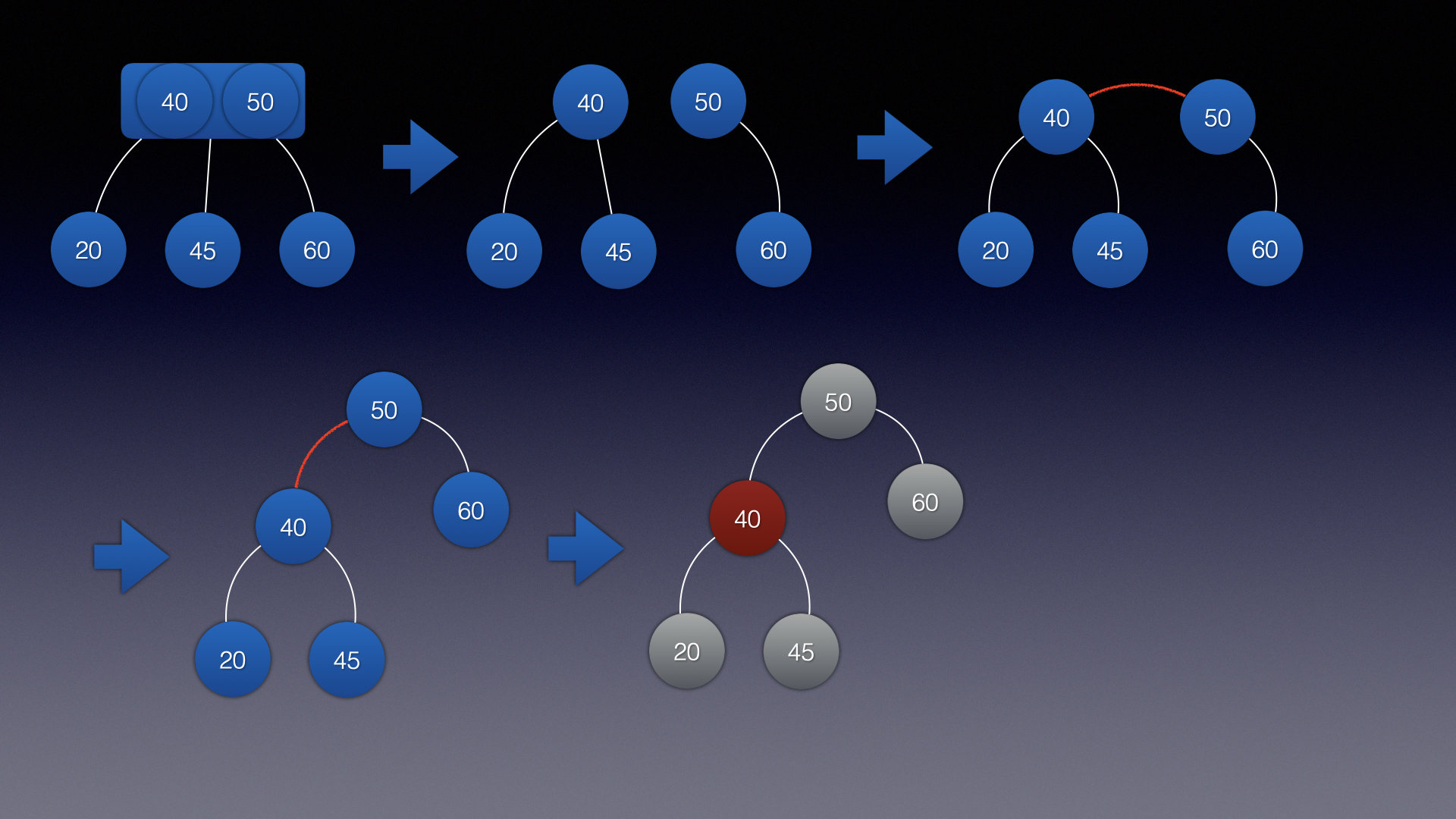
如果3叉树转变成红黑树也是同样的道理

先拆分成2个结点

• 第一个结点:40
• 第二个结点:50

在让第一个结点变成红色,第二个结点变成黑色即可

完整红黑树转变流程

使用的还是上面提到的数据:

步骤不分先后!

1. 先将2结点都变成黑色

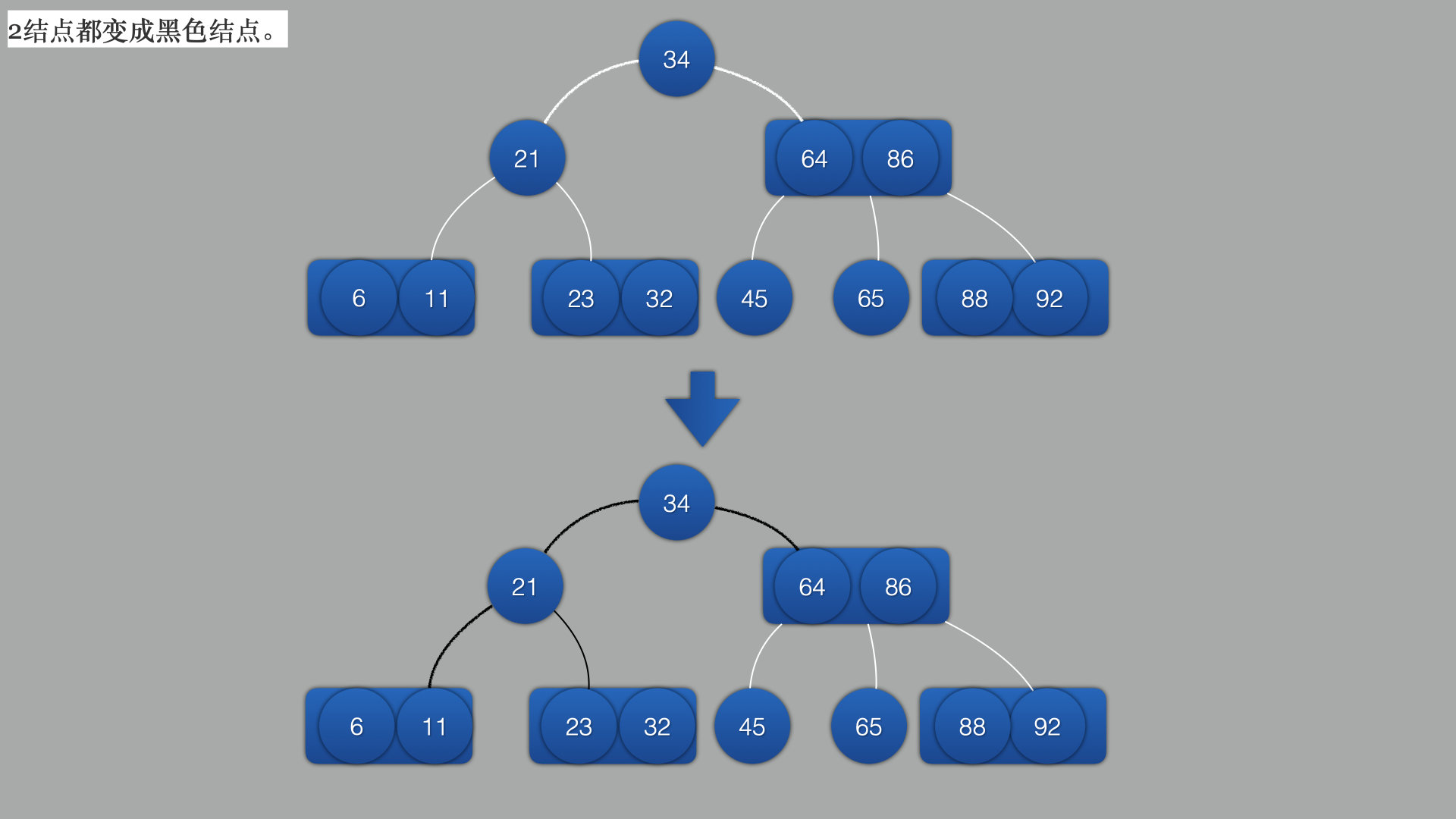
2. 将3结点拆分成2个结点,并且第一个结点为红色,第二个结点为黑色

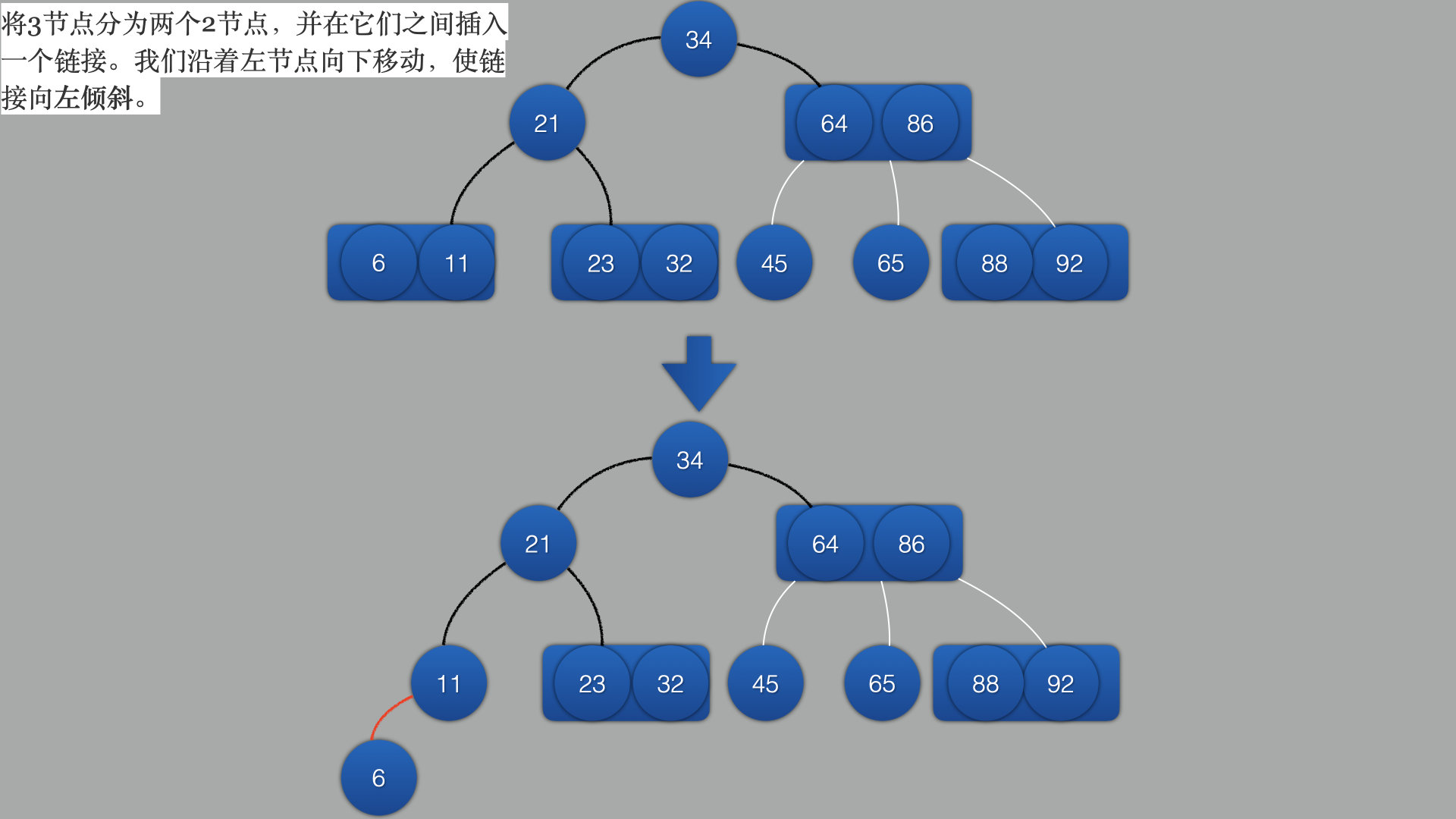
3. 相同逻辑:

   

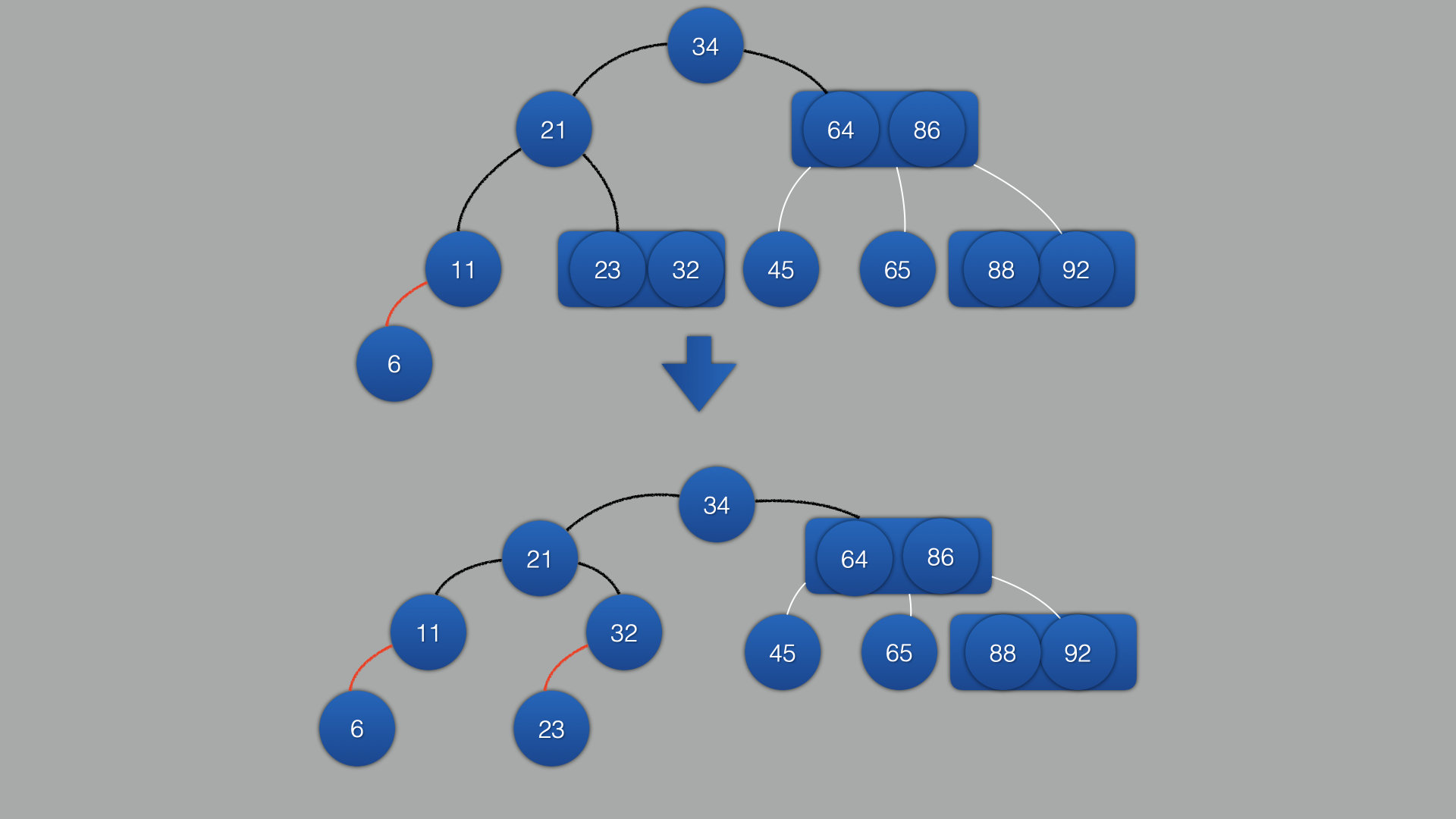
4. 相同逻辑
   

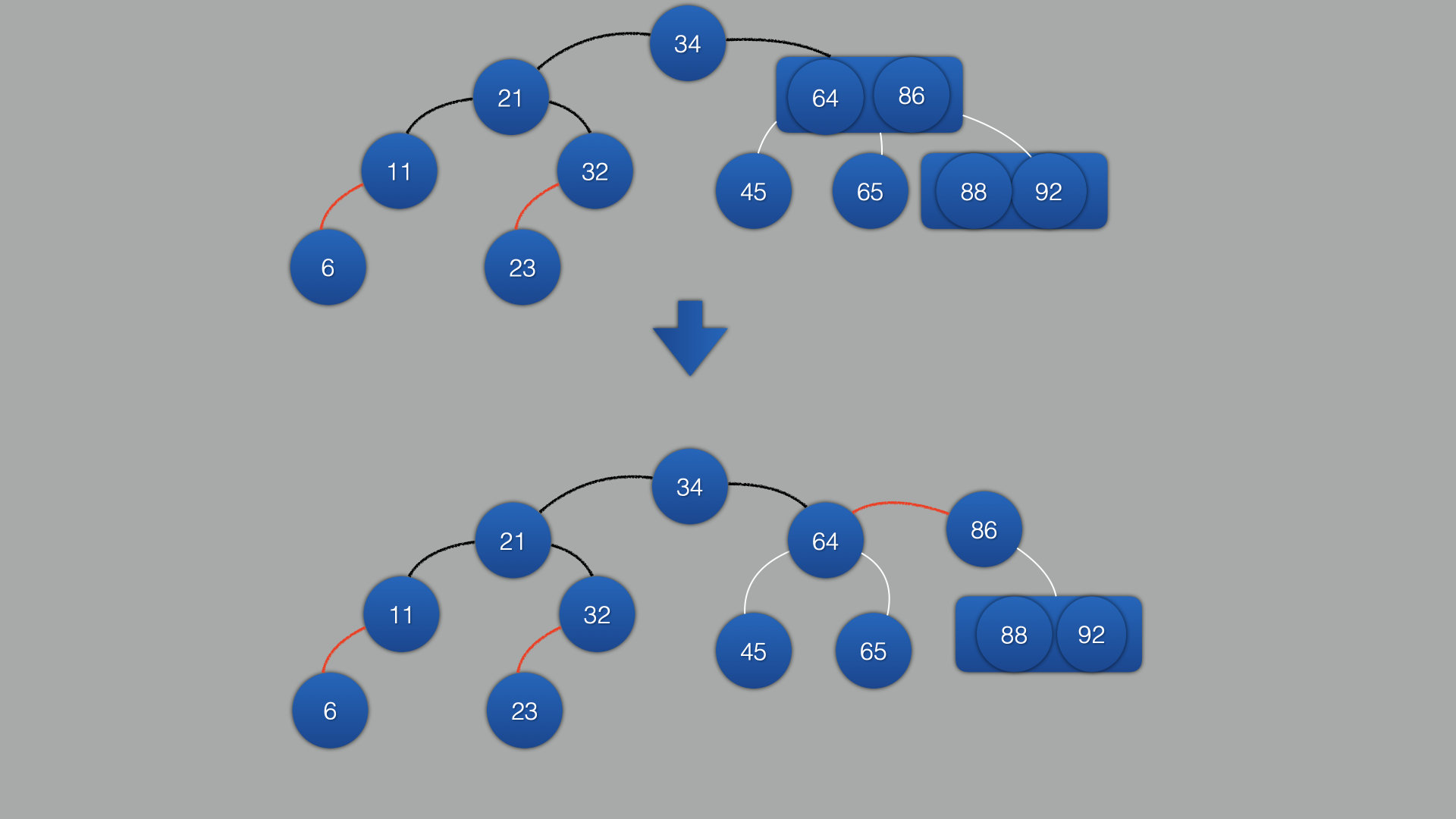
5. 将2结点都变成黑色
   

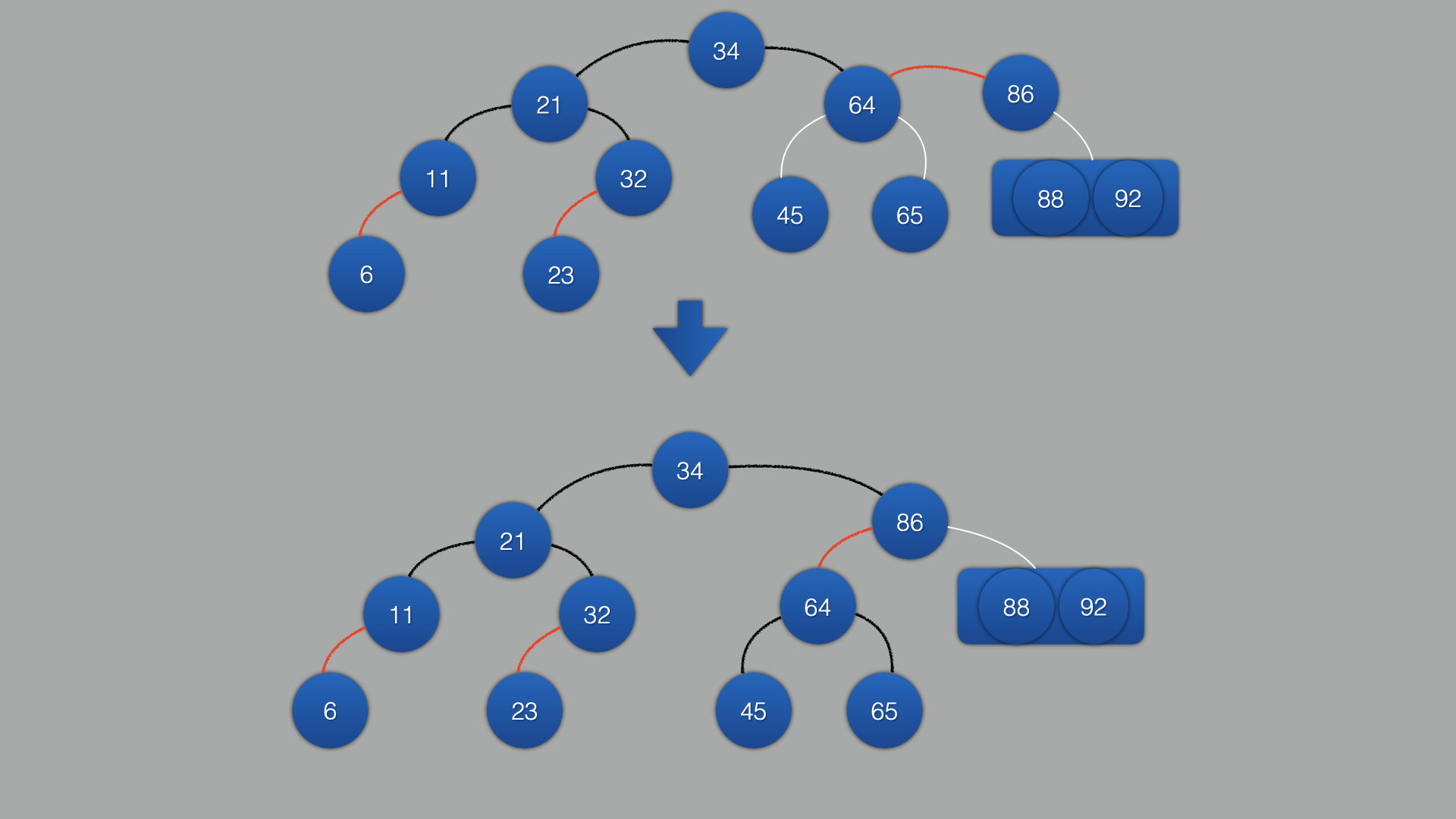
6. 相同逻辑
   

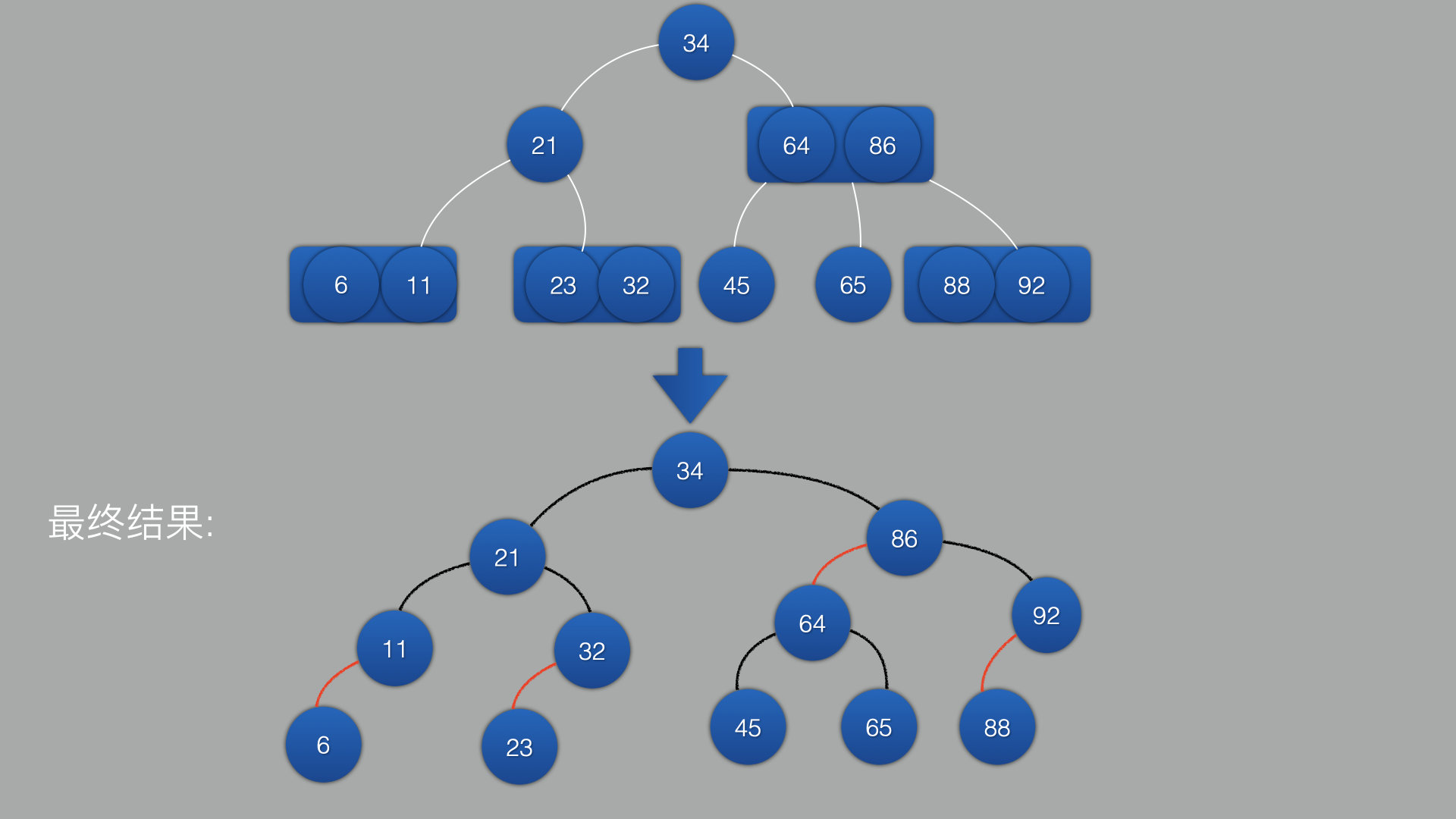
如果吧线替换成具体的颜色:

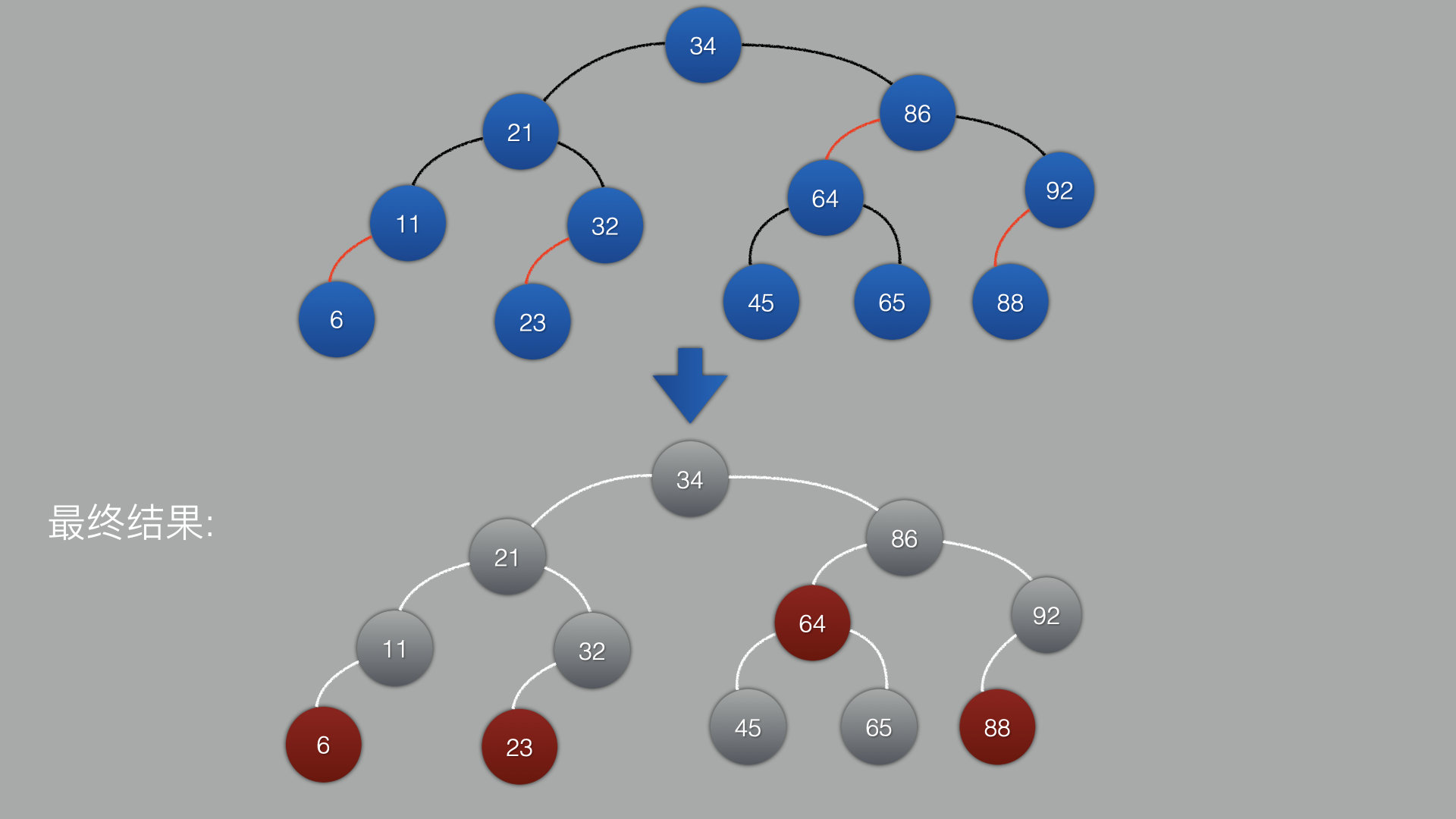
从最终结果来看,可以看出红黑树的特性:

• 根结点一定是黑色
• 根结点到每个叶子结点的黑色结点个数相同 (所以有红黑树也叫黑色平衡树的说法)
• 不存在2个相邻的红色结点 (红色结点不能有子结点是红色的)

也可以通过这些性质得到一些其他的性质:

• 如果父结点是红色,那么他一定有一个黑色的爷爷结点

还有一些隐藏特性:

其实真正的一棵树红黑树长这样:

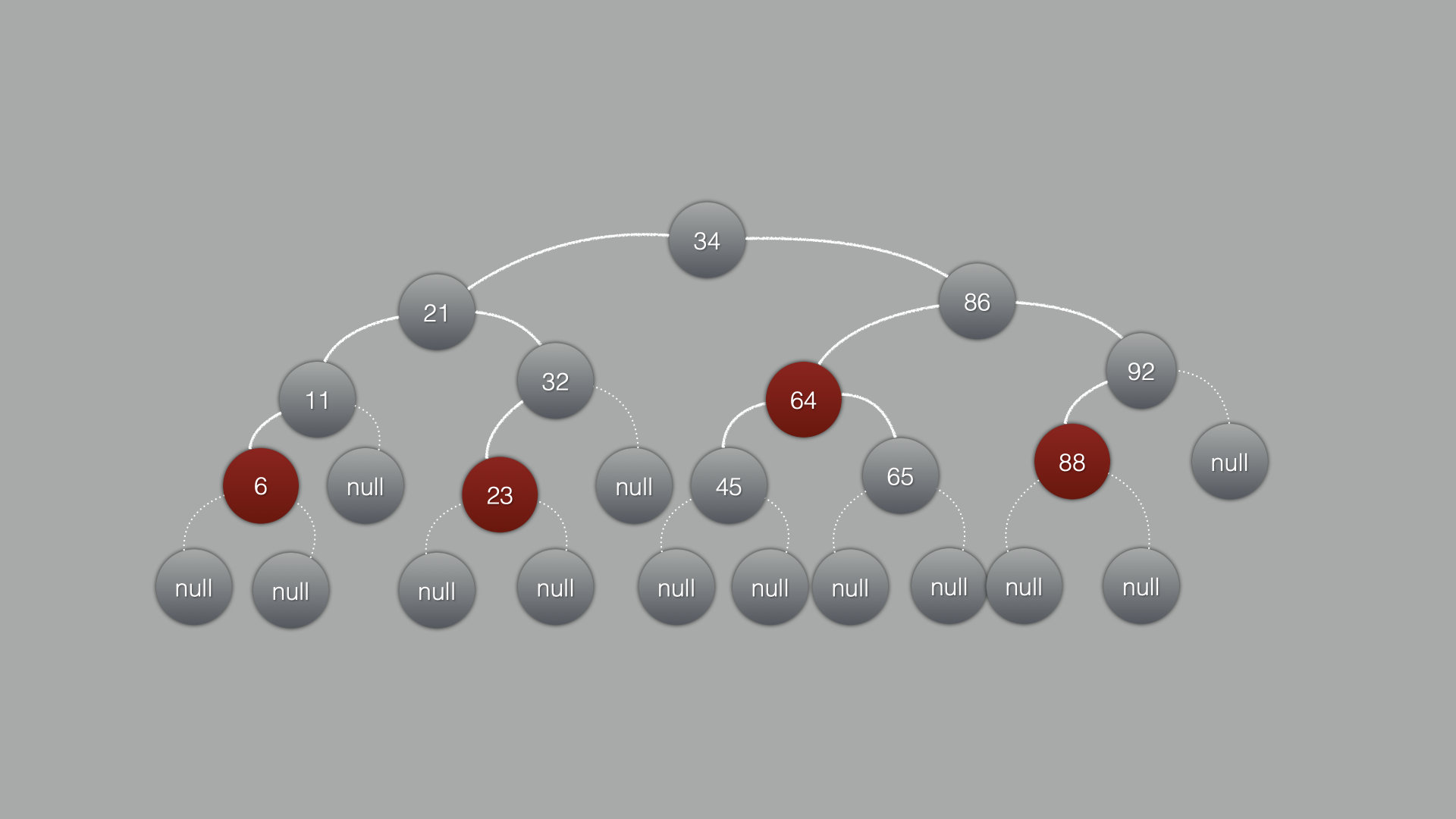
从这张图可以看出,叶子结点如果是null的话,那么就默认是黑色

并且底部结点都是黑色的!

这里红黑树就提这么多,等下一篇的时候,在详细聊一聊!

2-3-4树

如果理解了2-3树,那么2-3-4树就特别好理解

2-3-4树顾名思义就是

• 1个父结点 并且 2个子结点
• 2个父结点 并且 3个子结点
• 3个父结点 并且 4个子结点

说白了就是2-3树有的特性他都有,并且他比2-3树多一个4结点

插入

先看看完整流程:

插入结点和2-3树插入结点类似

• 2-3树是满3个结点然后拆分
• 2-3-4树是满4个结点然后拆分

还是取关键帧看一看:

关键帧1,2,3:

关键帧4,先拆分,在合并:

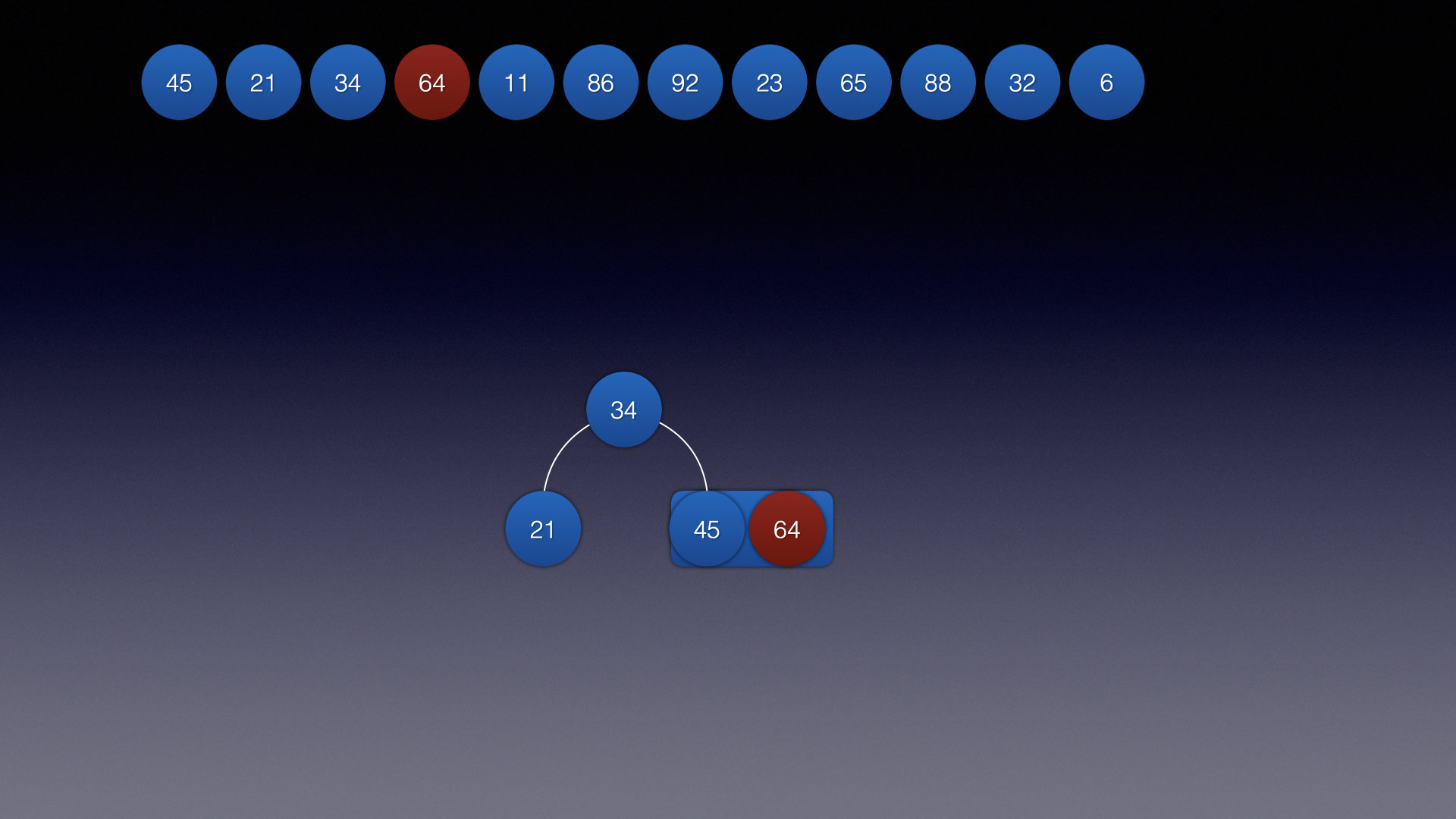
关键帧5,6:

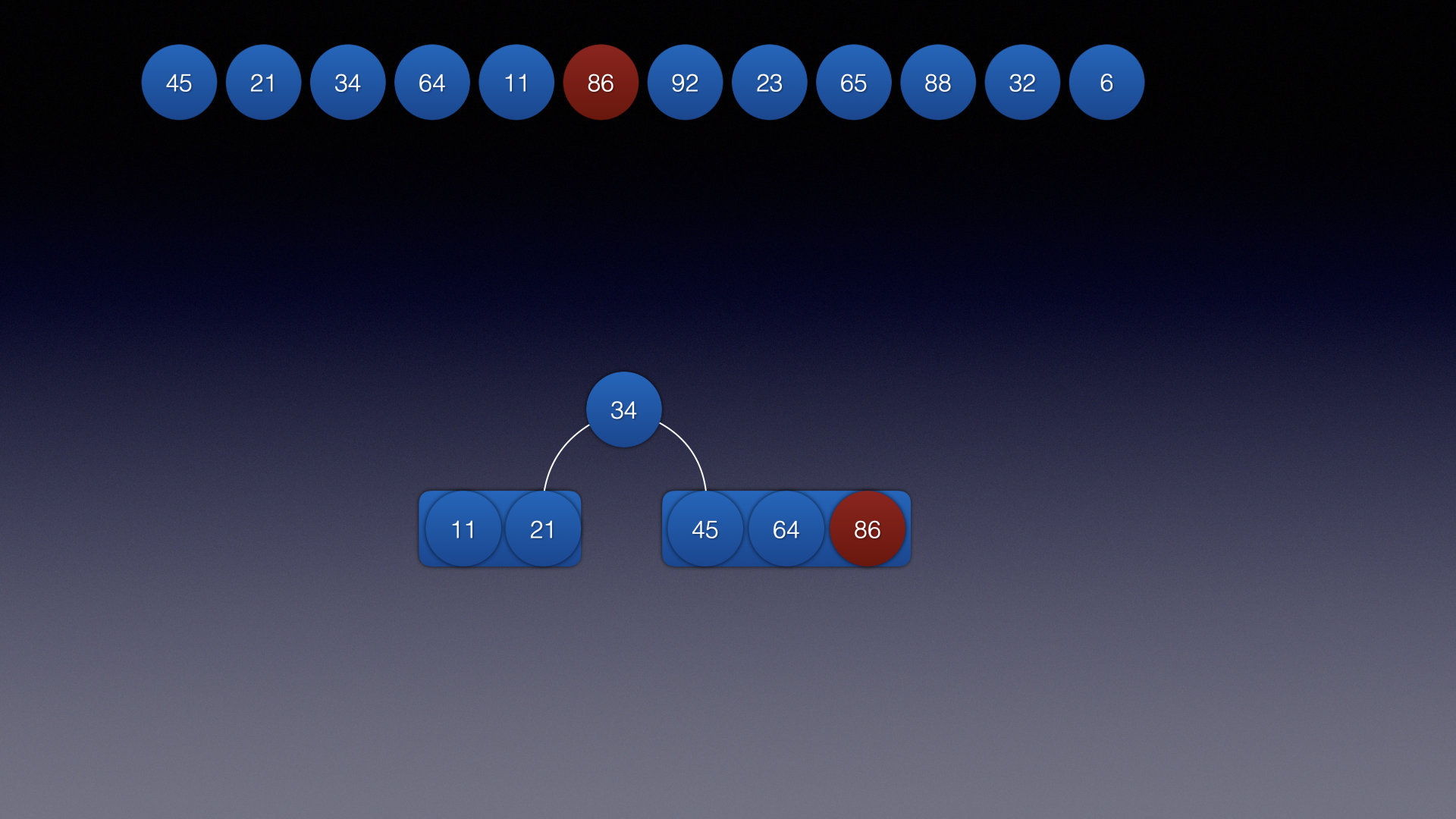
关键帧7:先拆分后合并:

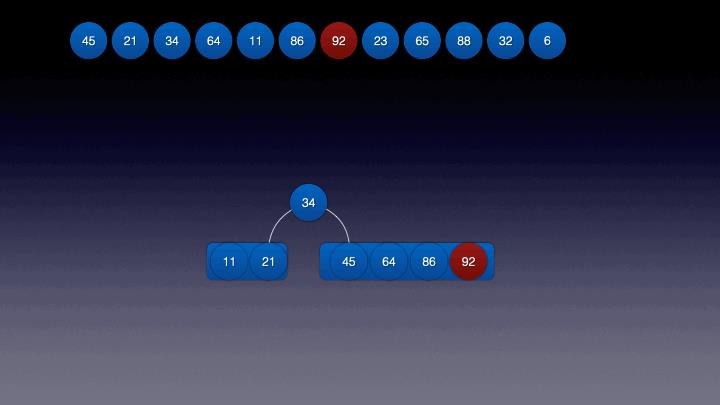
关键帧8,9:

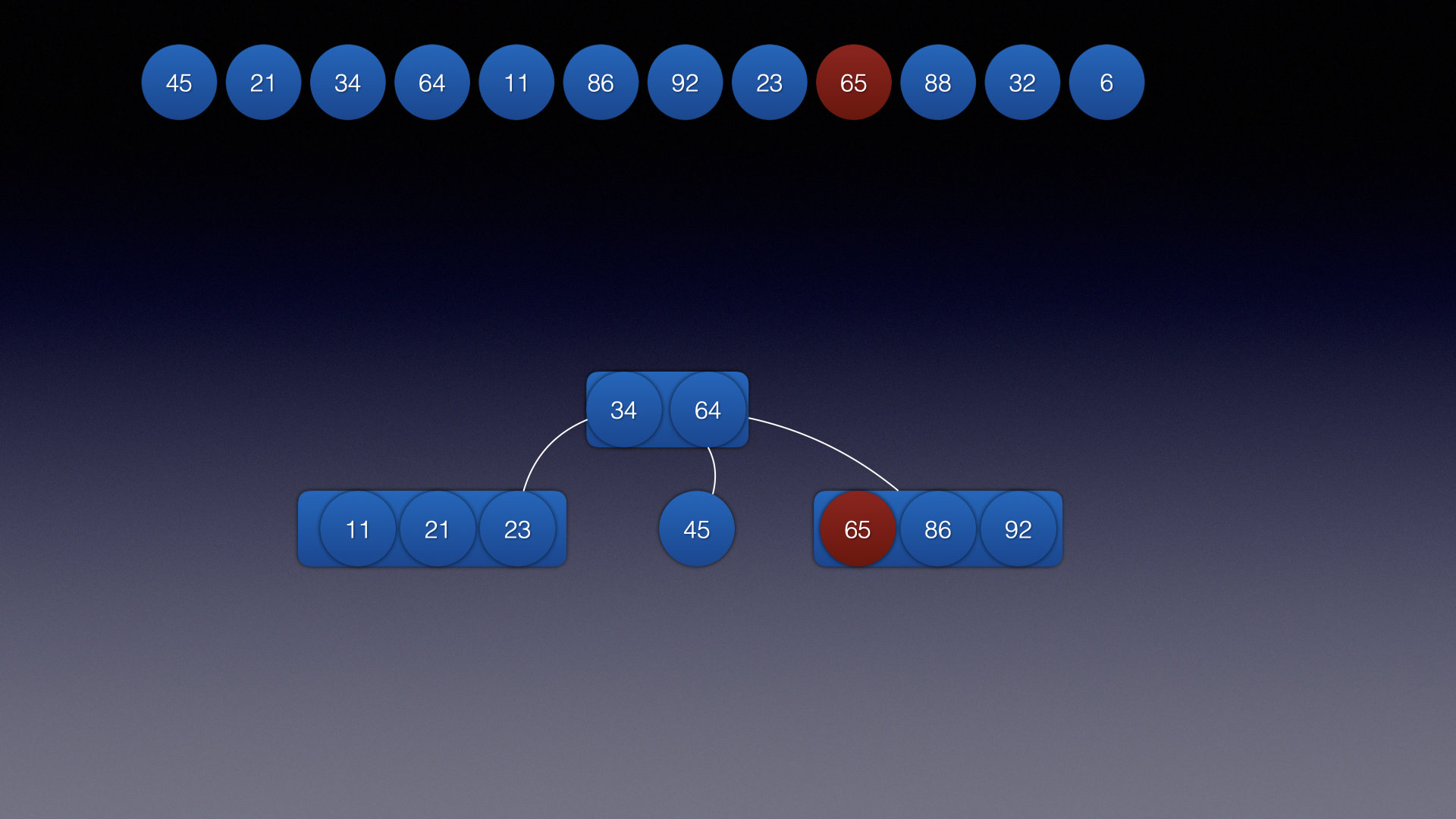
关键帧10:

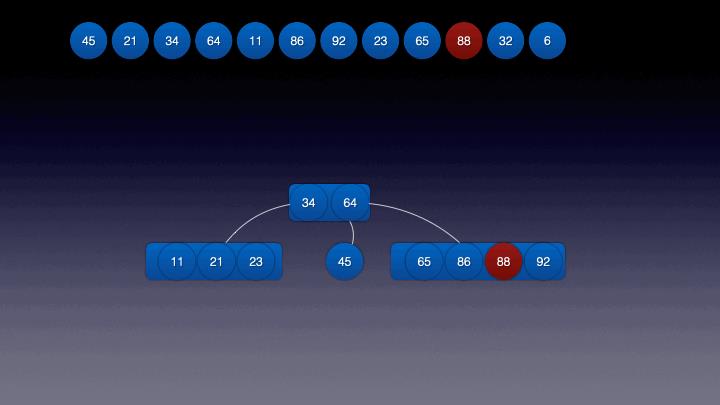
关键帧11:

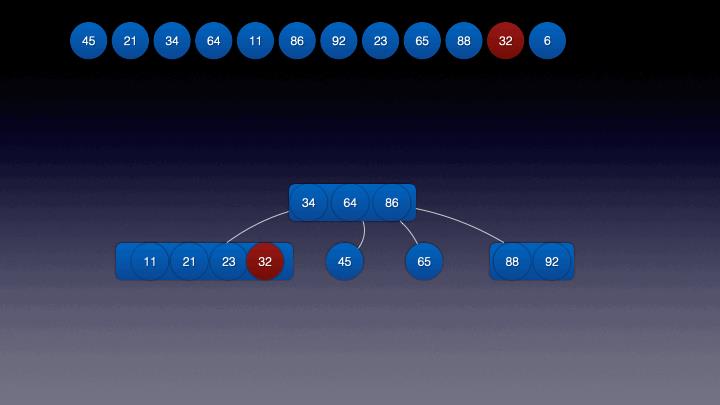
关键帧12:

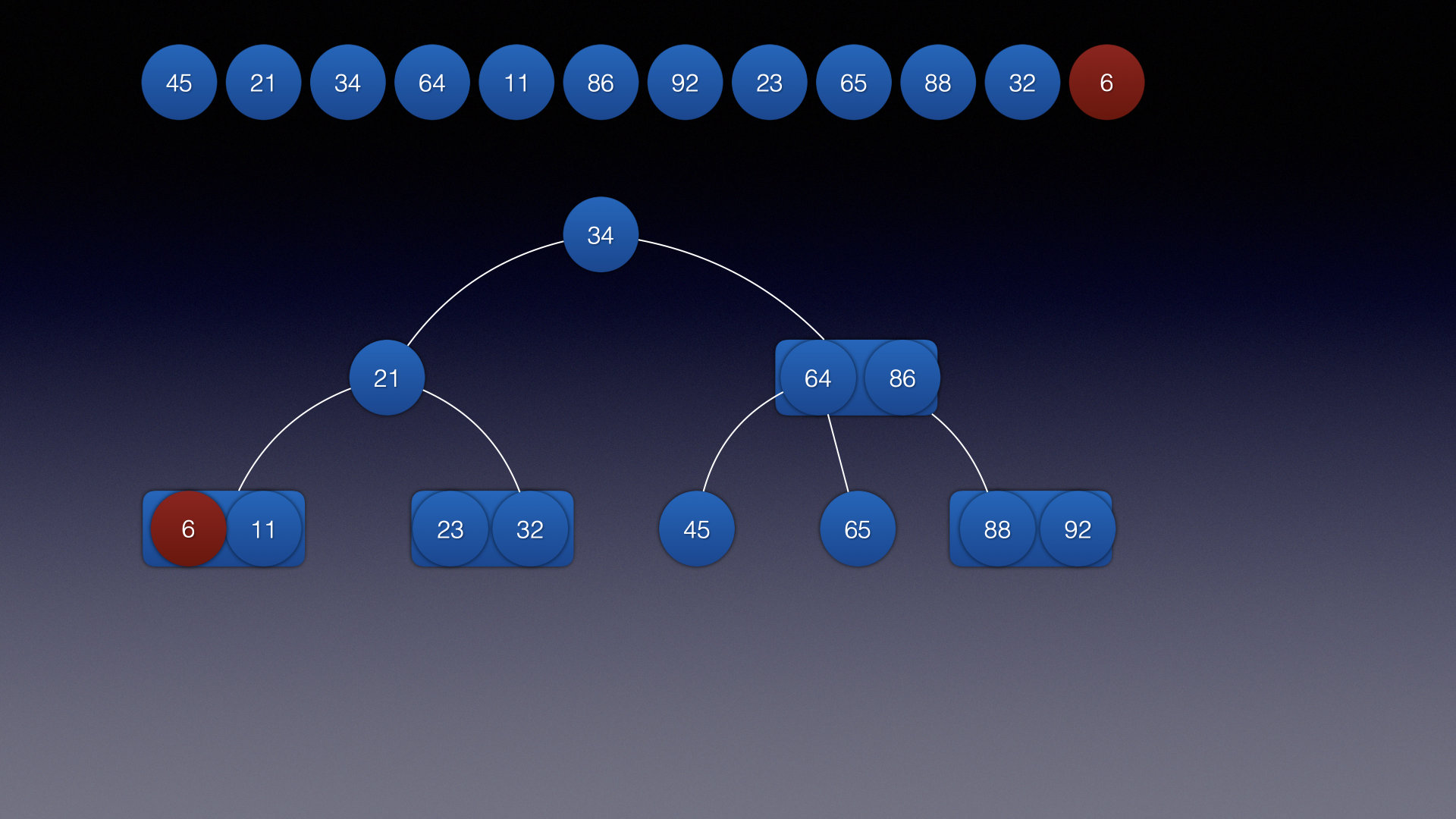
基本插入流程就是这样子…

删除流程就不说了,和2-3树基本类似…(主要是画图太累了…),而且讲了没啥用…代码太难写了,红黑树就是来代替2-3树 / 2-3-4树的,后续会有手写红黑树.

2-3-4树和红黑树的映射

基本映射方式有2种情况:

情况1:

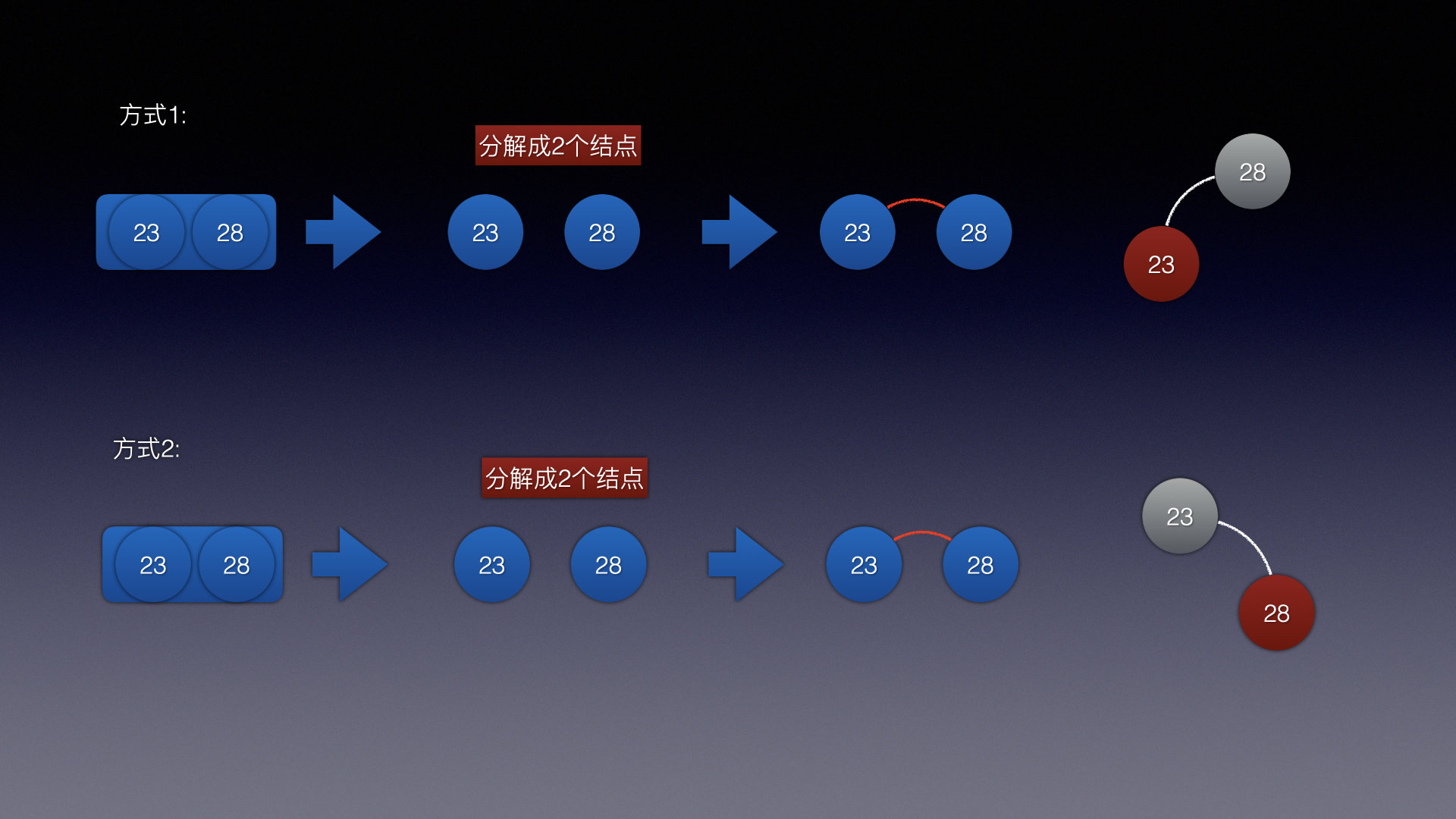
情况2:

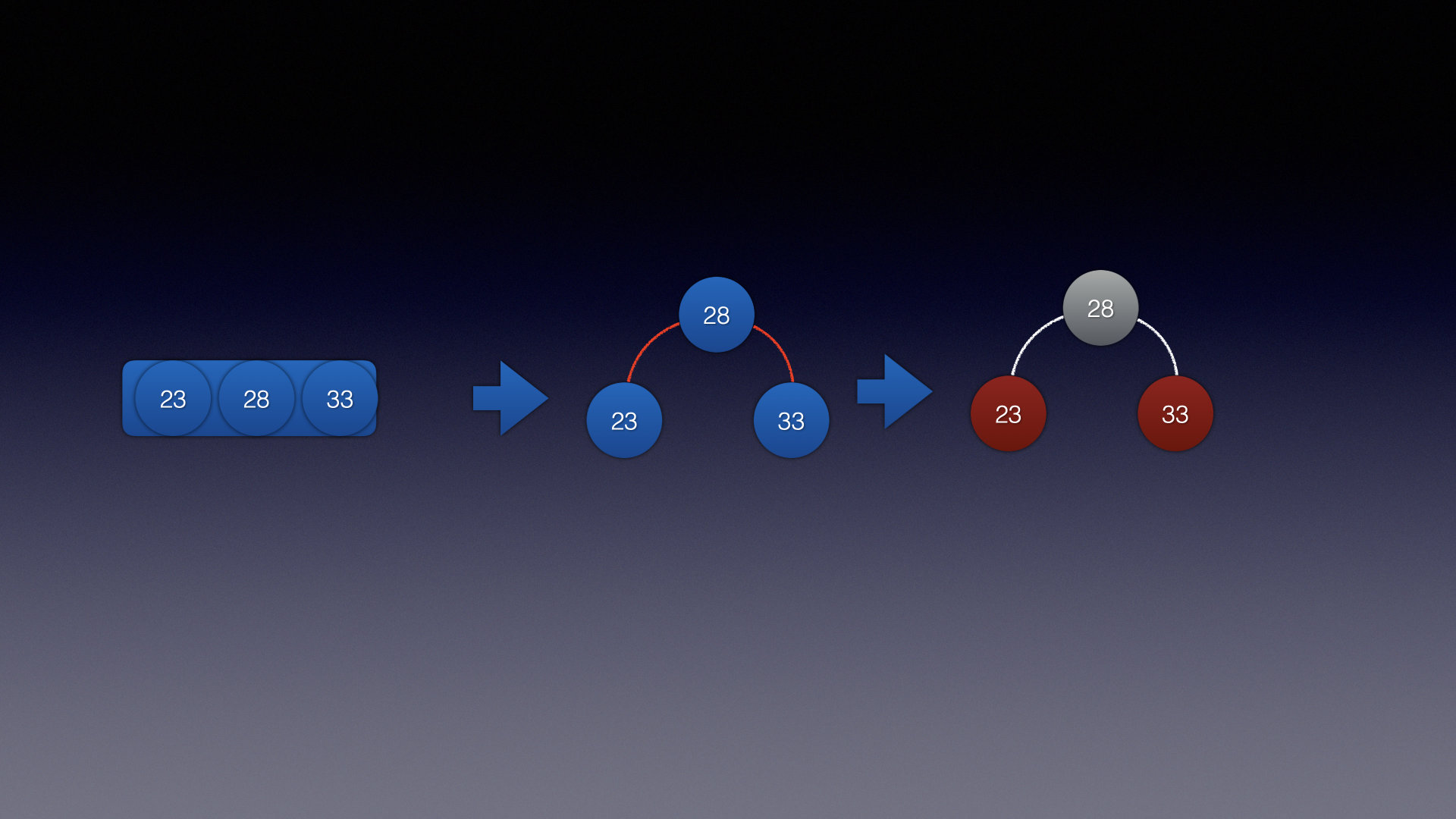
还是使用上面的数据,并且多加一点数据,来看看转变成红黑树后是什么样子:

1. 还是和2-3树一样,将所有2个结点的都连接成黑色

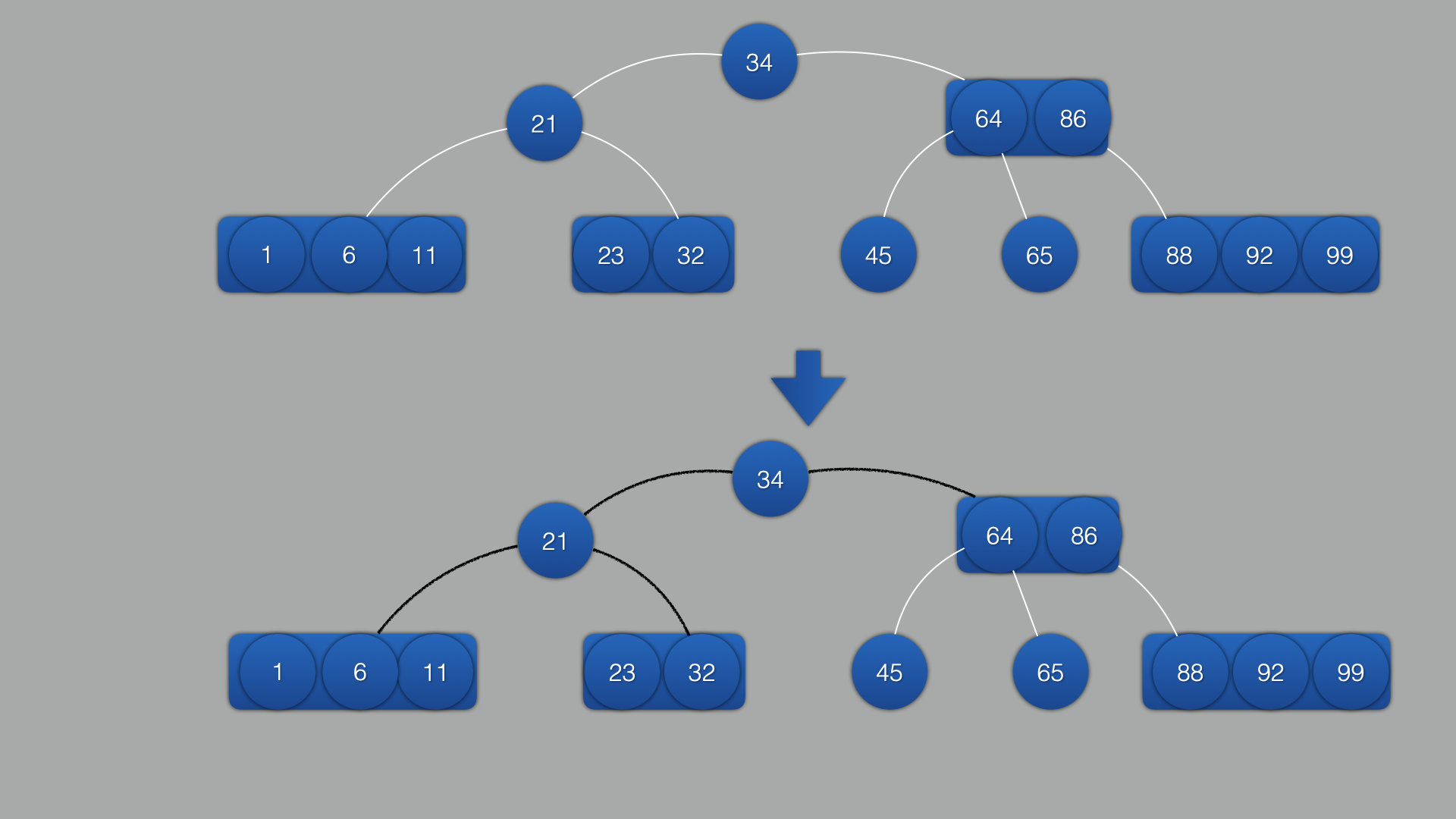
2.将所有4叉树拆分成2叉树,以中结点为根结点,左右2个结点为红色

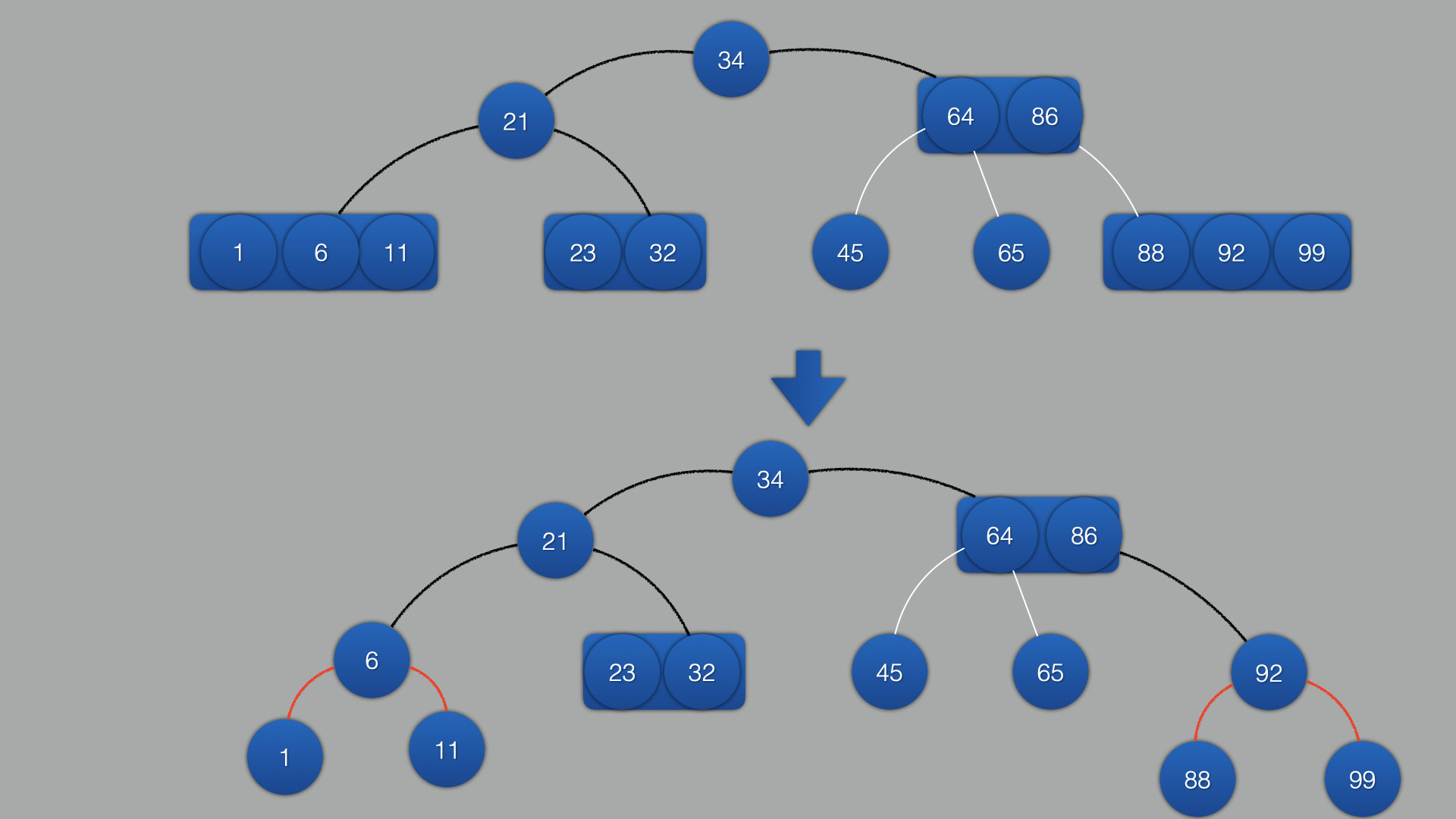
3. 将剩余2叉树拆分开,并且左子结点为红色

   

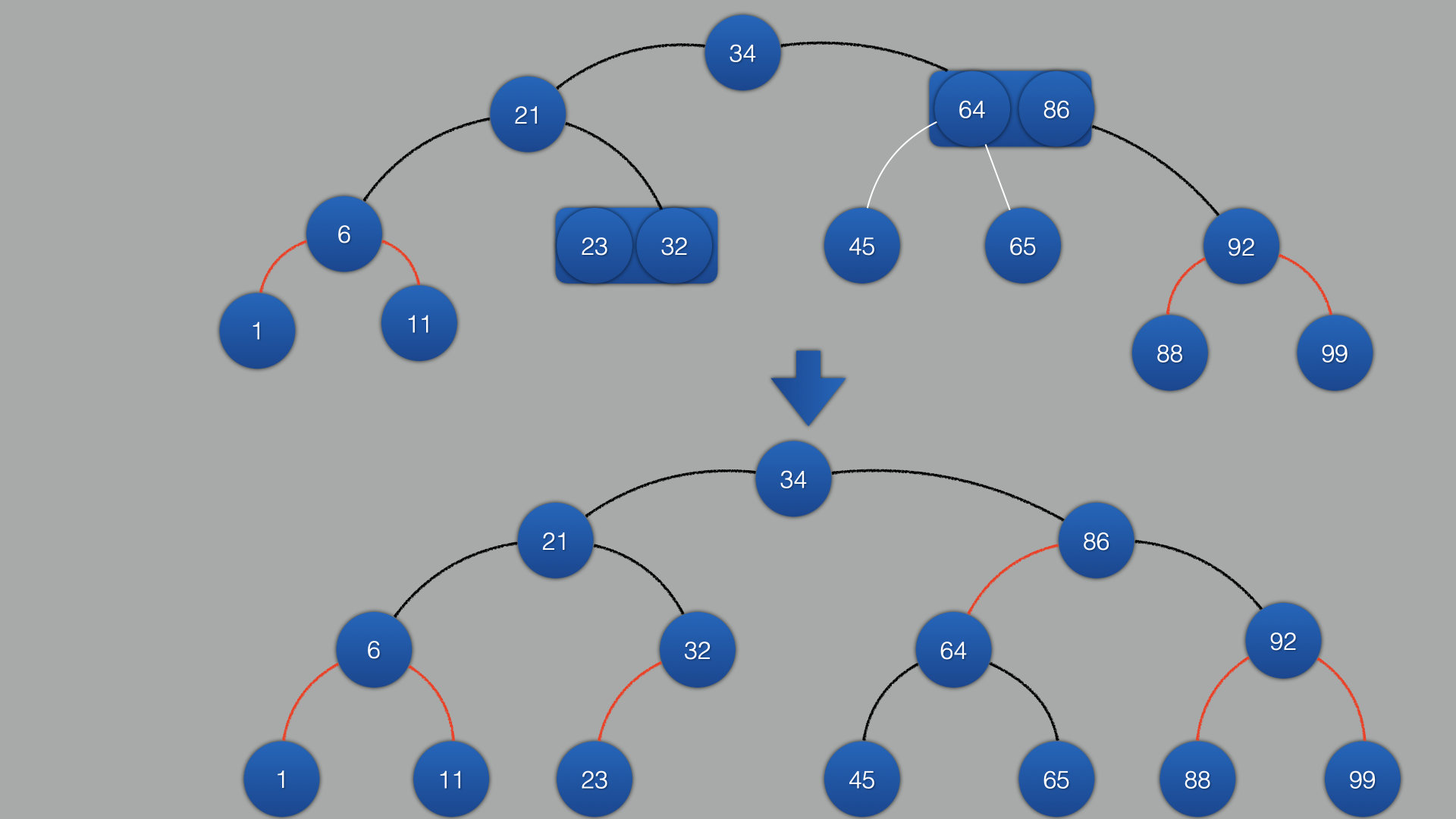
4. 最终效果:

   

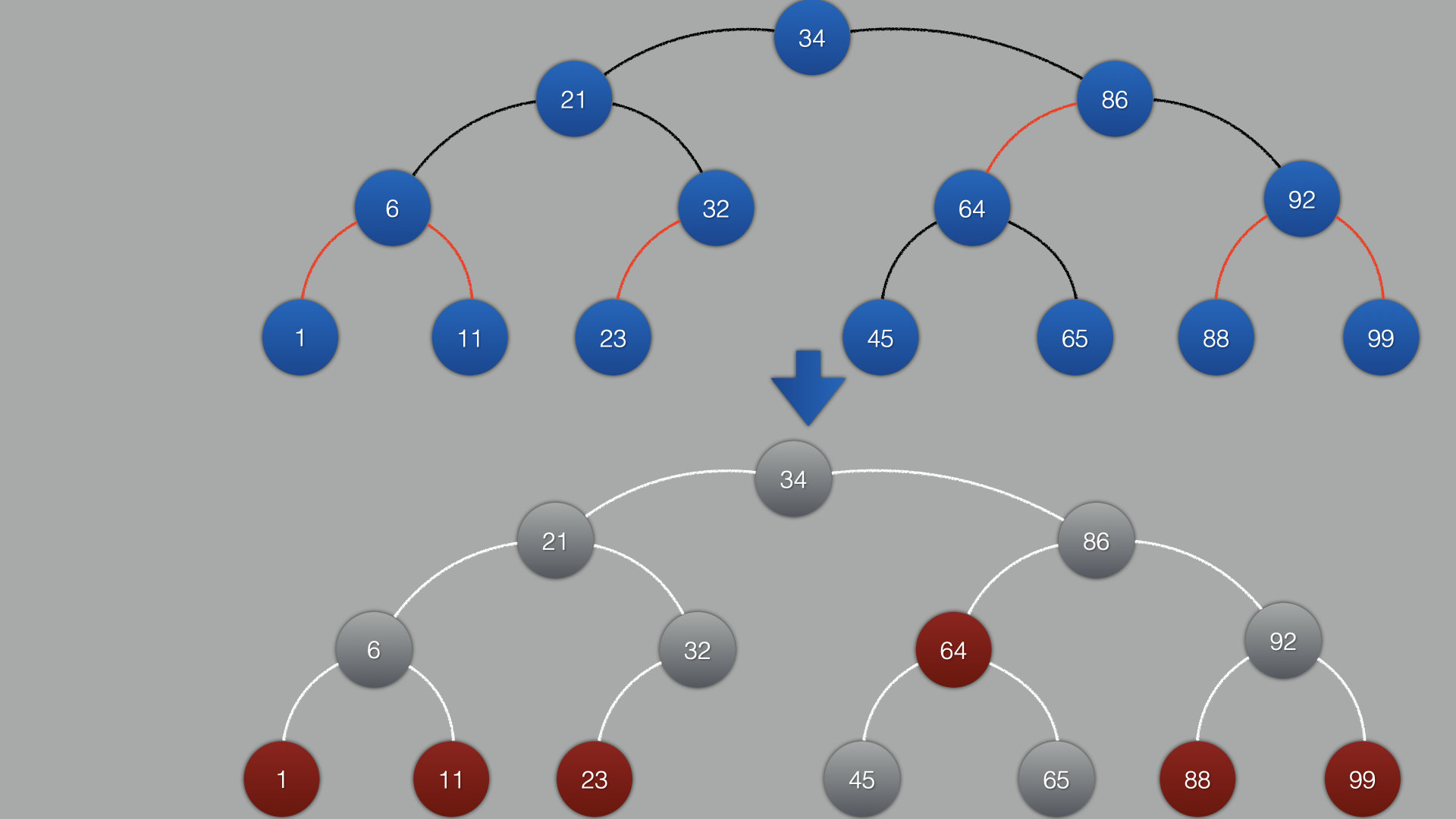
从最终结果来看,特性和2-3树一模一样 可以看出红黑树的特性:

• 根结点一定是黑色

• 根结点到每个叶子结点的黑色结点个数相同 (所以有红黑树也叫黑色平衡树的说法)

• 不存在2个相邻的红色结点 (红色结点不能有子结点是红色的)

• 如果父结点是红色,那么他一定有一个黑色的爷爷结点

B树 B+树 B*树

本来想写这个的,但是网上一看,基本说的都一样,并且对红黑树没啥用,本系列最重要的就是红黑树,所以就推荐几篇我认为好的文章看看吧!!

远古大牛文章

老外文章,可能需要用梯子

完整代码

原创不易,您的点赞就是对我最大的支持!

其他树结构文章:

1. 二叉树入门
2. 顺序二叉树
3. 线索化二叉树
4. 堆排序
5. 赫夫曼树(一)
6. 赫夫曼树(二)
7. 赫夫曼树(三)
8. 二叉排序树(BST)
9. 平衡二叉排序树AVL
10. 2-3树,2-3-4树,B树 B+树 B*树 了解 本篇
11. 数据结构与算法:树 红黑树 (十一)