计算机视觉中的深度学习5: 神经网络

Posted 2022-12-03 SuPhoebe

Slides：百度云 提取码: gs3n

前情回顾

我们讲解了

1. 用线性模型进行图片分类
2. 用Loss函数来表示不同的权重的好坏
3. 用SGD来训练模型，使得Loss函数最小

新的挑战

线性分类并不能解决一切问题

比如，下图的非线性分类问题

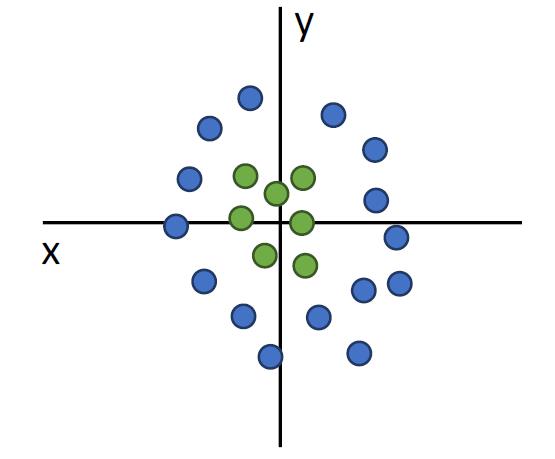
再比如，对于每个类别，都需要一个模板来表示，从而它不能识别一个类中其他状态的图片。

特征转化

用如图的方式进行极坐标和直角坐标的转化，从而使得右图是线性可分的

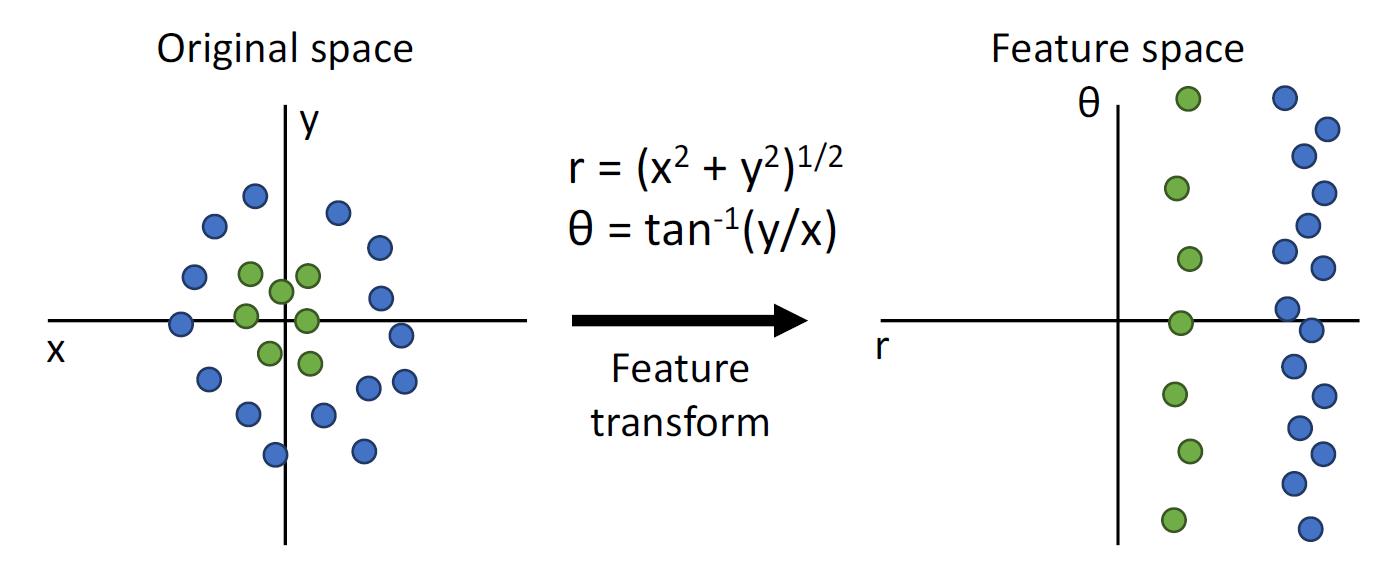
图片特征：颜色直方图

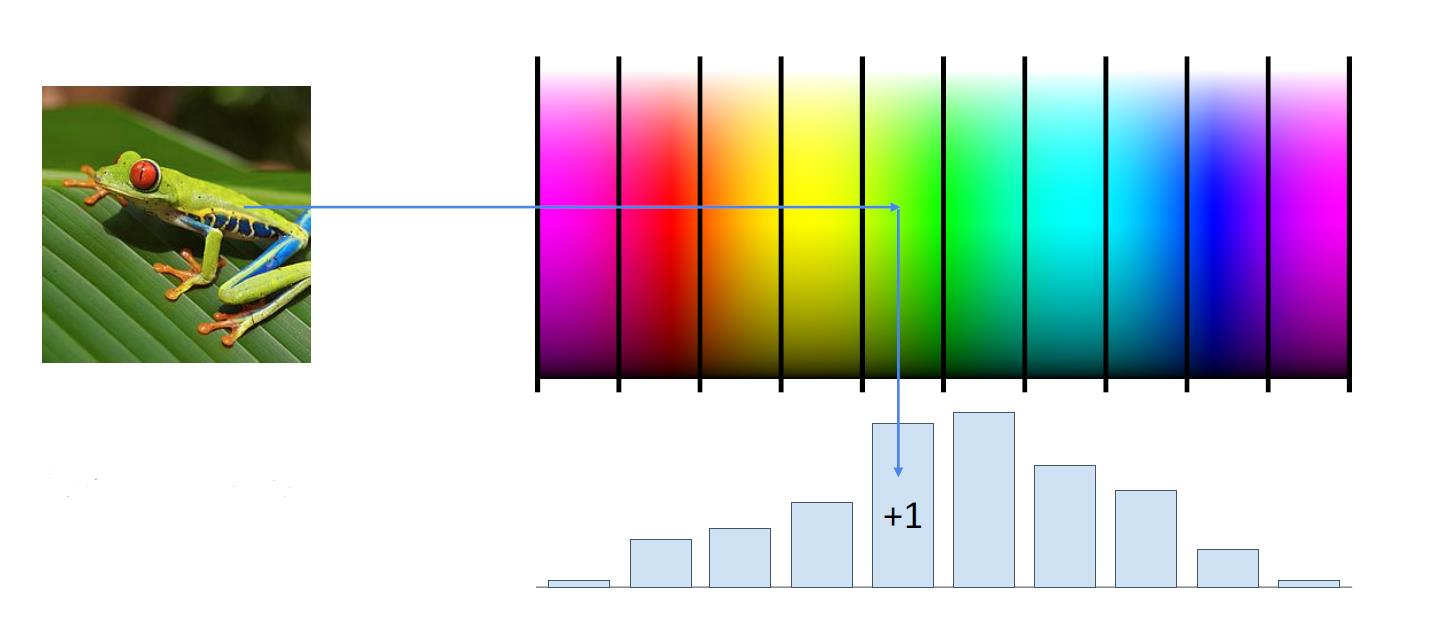
将图片进行统计学意义上的特征提取

图片特征：边缘梯度直方图

用到了经典CV边缘判断，计算一个区域内边缘方向和边缘长度的乘积，形成一个新的直方图。

还有其他方式，这些特征提取需要极多的图片识别背景知识，也需要很多脑洞。

而且他们的效果也非常不错，在2011年的ImageNet 挑战赛里，优胜者就是使用的各种图片特征提取的方式

图片特征提取 vs 神经网络

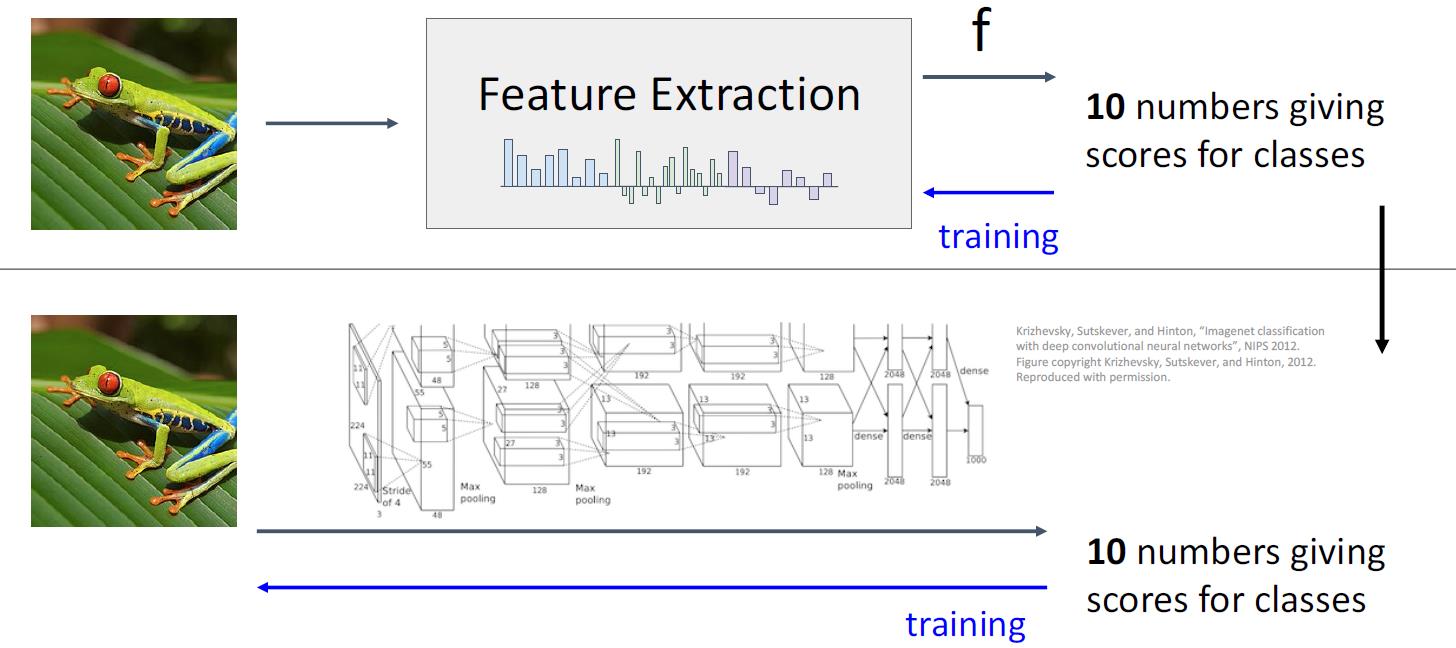
两者有着异曲同工之效，特征提取是人类通过自身知识进行提取，而神经网络是通过神经网络自行对特征进行提取。对于后者而言，人类经常不能知道神经网络提取的是哪个特征，也不能知道神经网络为什么要这样提取特征。

神经网络的本质就是通过AI代替人类进行特征提取的过程。

神经网络

对于一个两层的全连接神经网络，他的公式如下

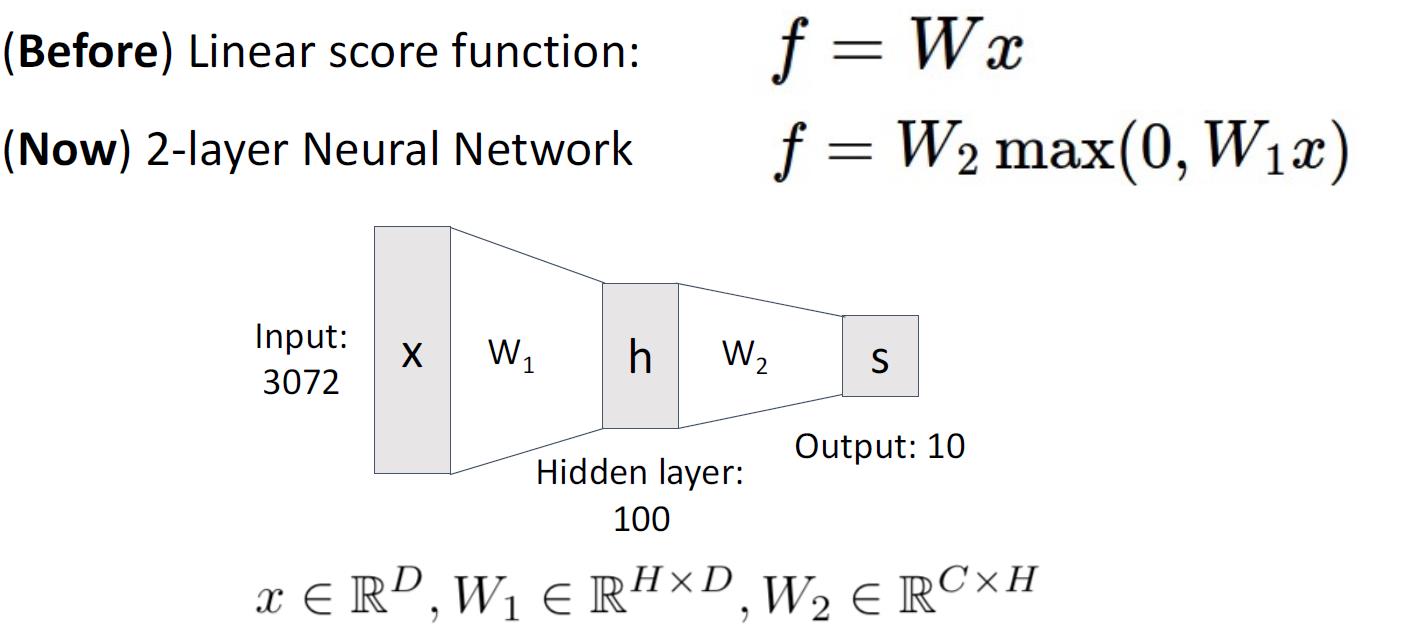
实例

import numpy as np
from numpy.random import randn

N, Din, H, Dout = 64, 1000, 100, 10
x, y = randn(N, Din), randn(N, Dout)
w1, w2 = randn(Din, H), randn(H, Dout)
for t in range(10000):
    h = 1.0 / (1.0 + np.exp(-x.dot(w1)))
    y_pred = h.dot(w2)
    loss = np.square(y_pred - y).sum()
    dy_pred = 2.0 * (y_pred - y)
    dw2 = h.T.dot(dy_pred)
    dh = dy_pred.dot(w2.T)
    dw1 = x.T.dot(dh * h * (1 - h))
    w1 -= 1e-4 * dw1
    w2 -= 1e-4 * dw2

深度神经网络

即神经网络层数特别多

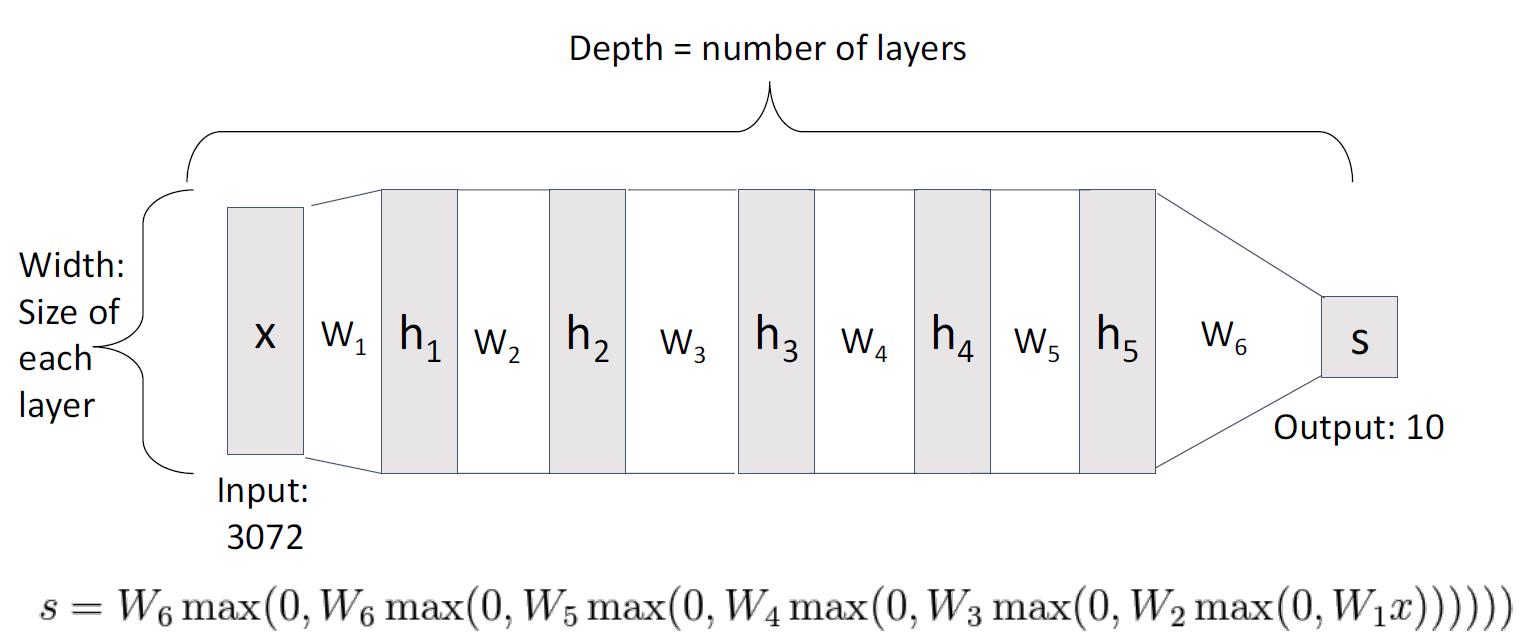
作用

能用多种类型的特征模板来识别一个类的不同模式，如上图所示，就是一个180°镜面反转的效果。

激活函数

人体神经元的工作状态是：刺激到达一定阈值后，神经元才发送神经信号。那么在神经网络中，激活函数就是同样的功能，用来描述输出的神经信号。

这里介绍一个极其通用的，甚至可以说是在大多数情况下的默认函数$ReLu(x)$

$$ReLu(x)=max(0,x)$$

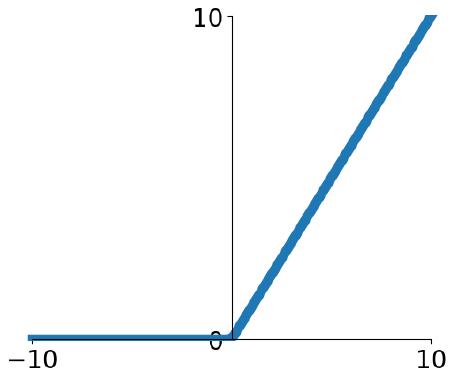
则输出为

$$f=W_{2}max(0,W_{1}x)$$

常用的激活函数

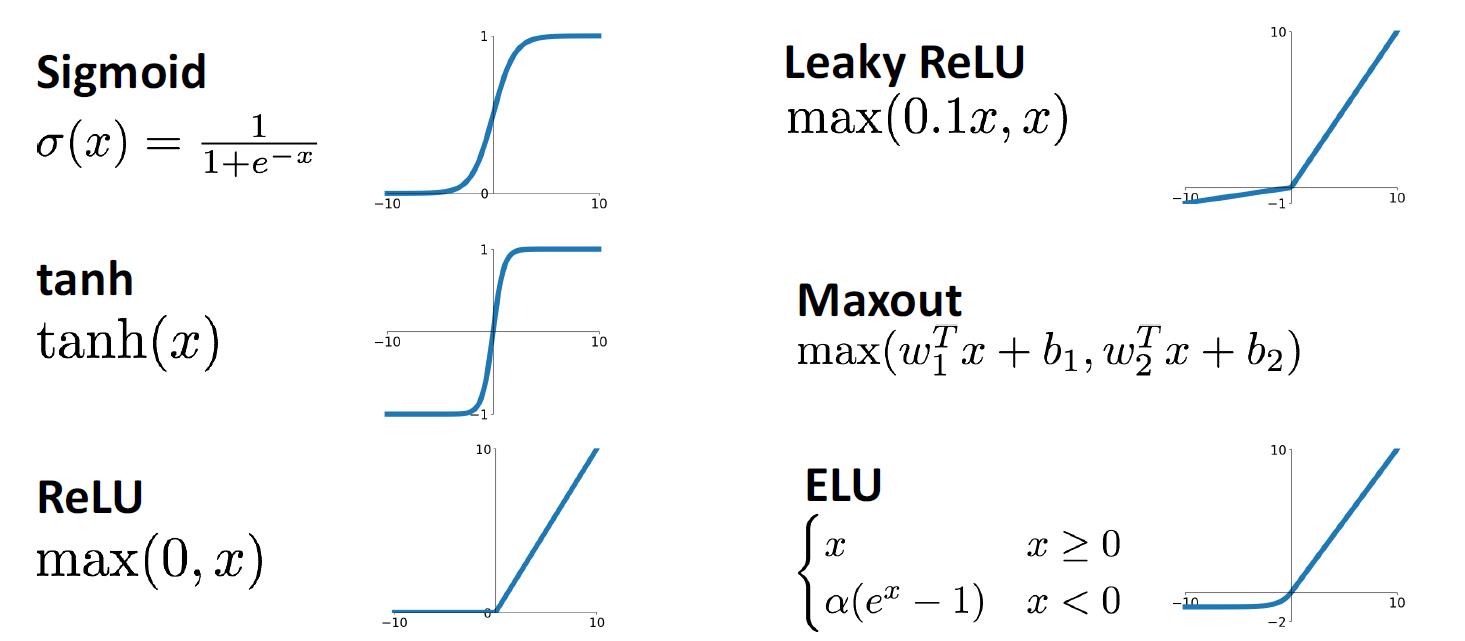
空间扭曲

没有激活函数

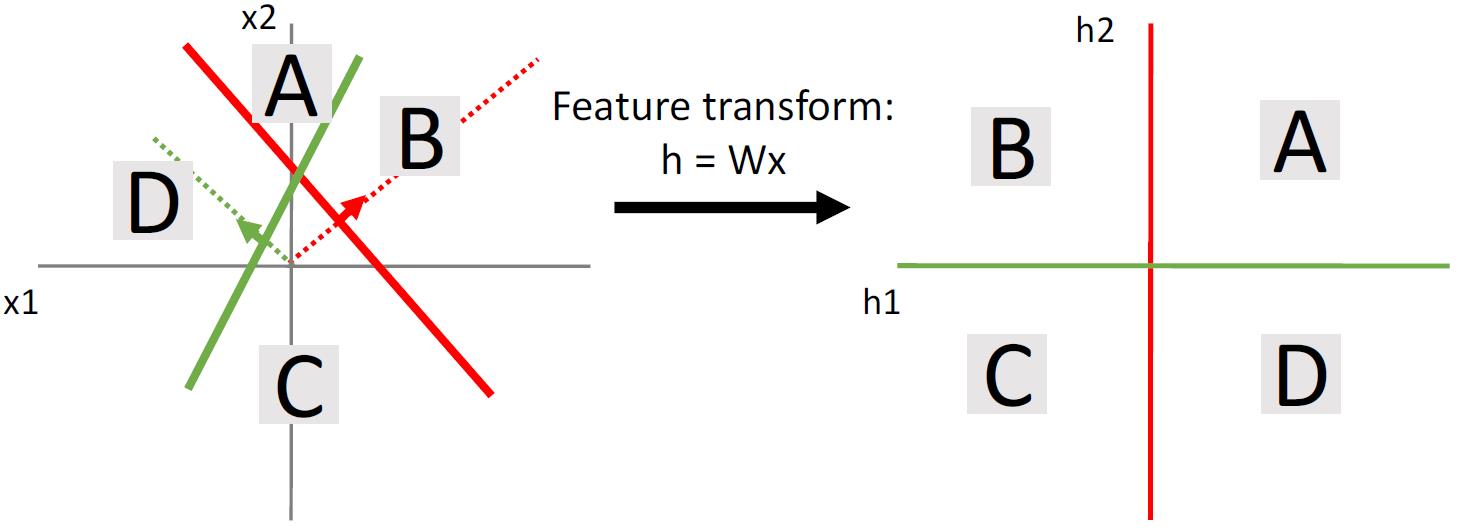
通过特征提取，我们能做到简单的空间划分，但是这样的空间划分，有点时候并不是那么有效。

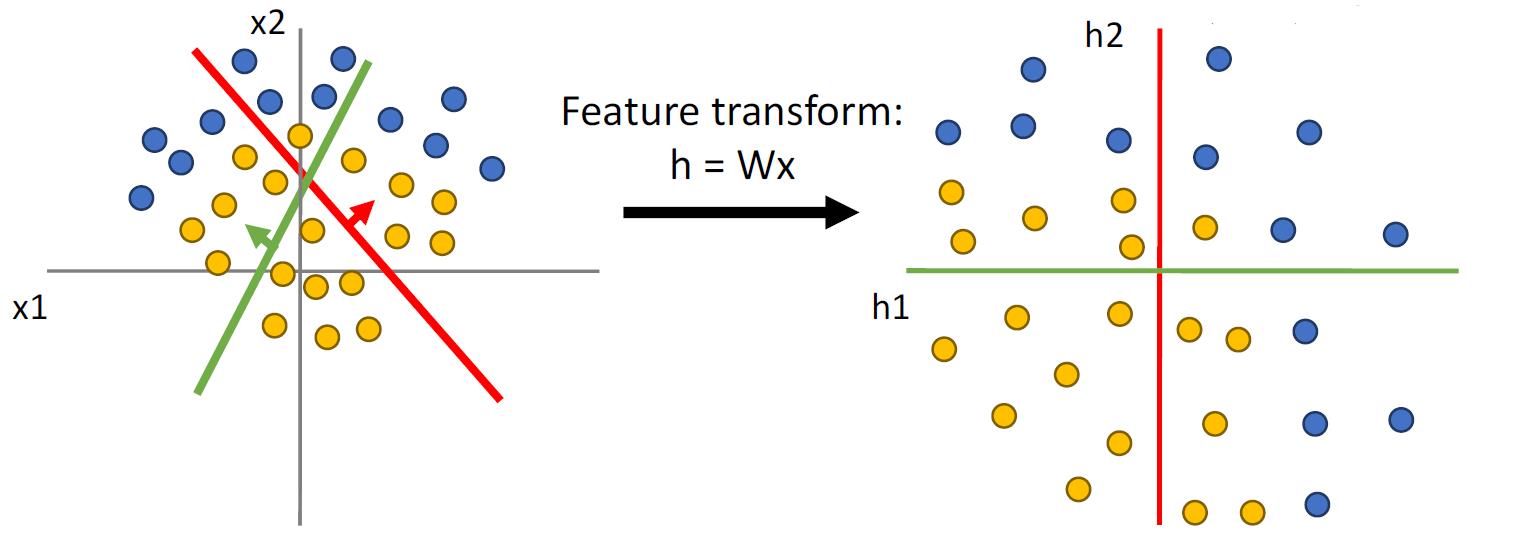
下图进行了类似的空间转化，但是还是不能使得样本线性可分。

使用激活函数

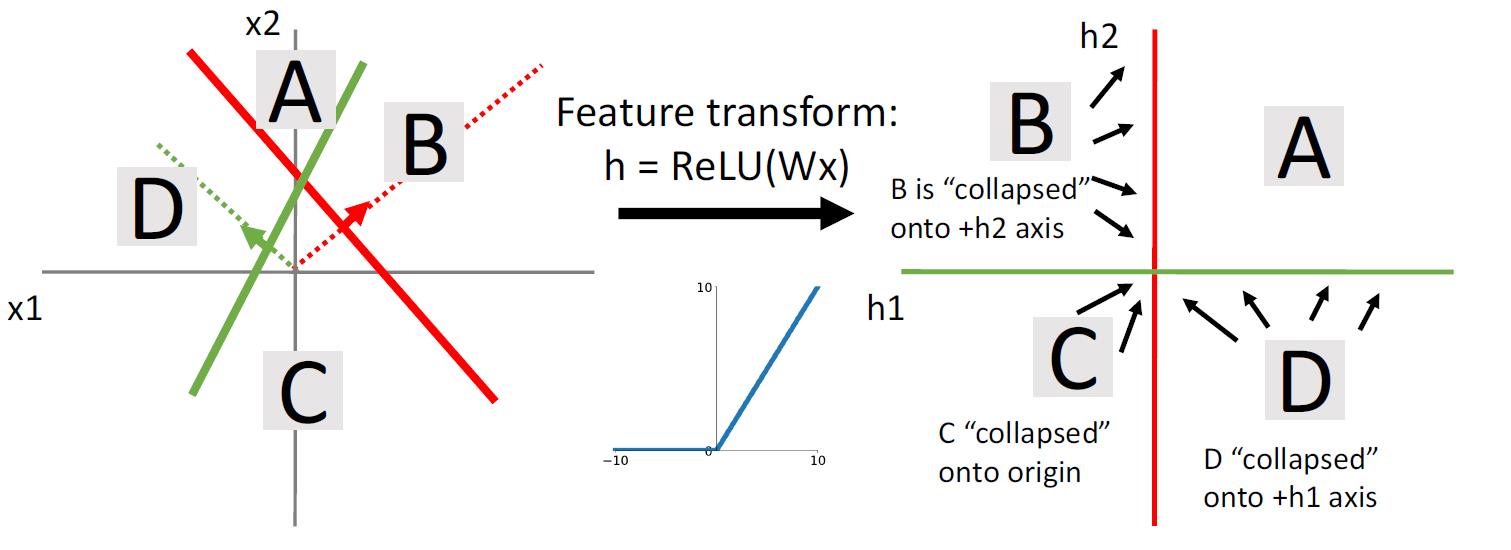
使用激活函数后，B聚集于Y轴上半部分，C聚集于原点，D聚集于X的右半部分。

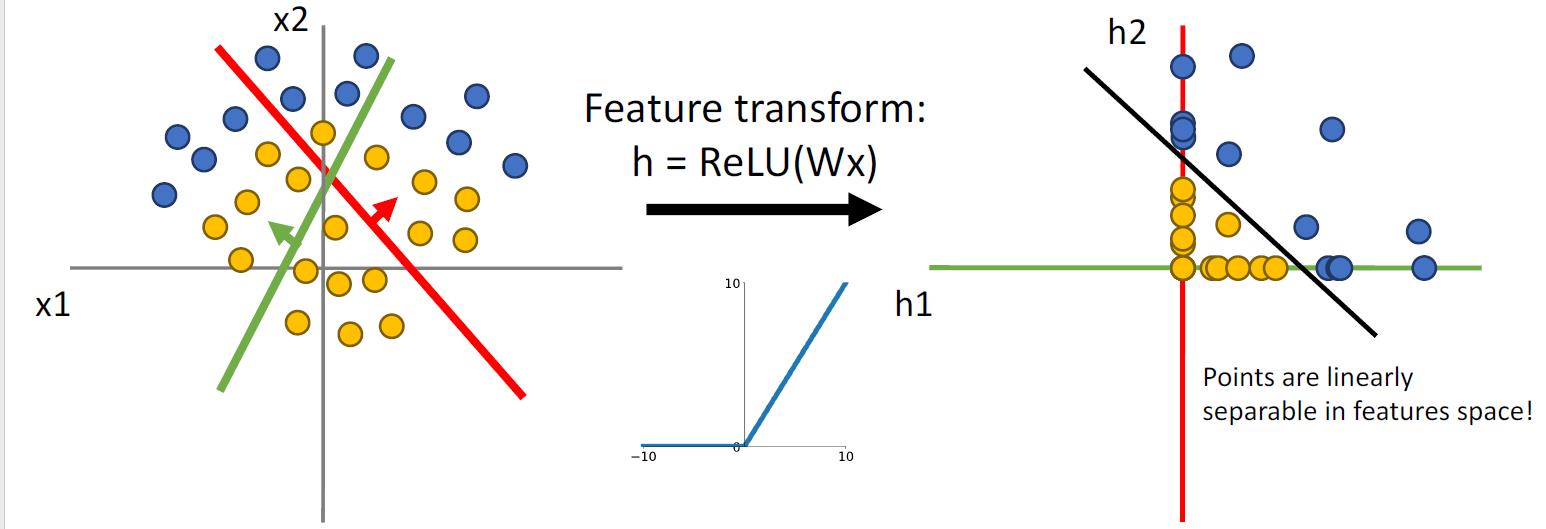
隐层单元个数

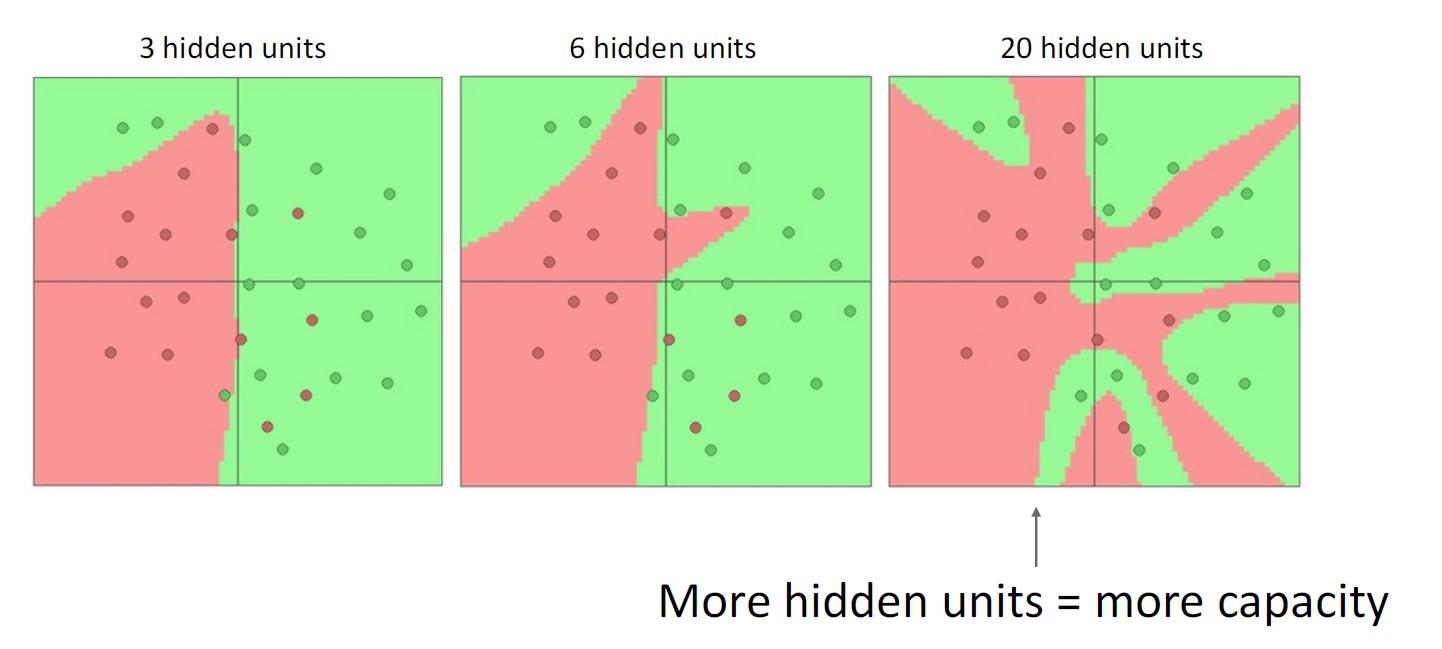
隐层的数量越多，就能更准确地识别每一个训练样本。

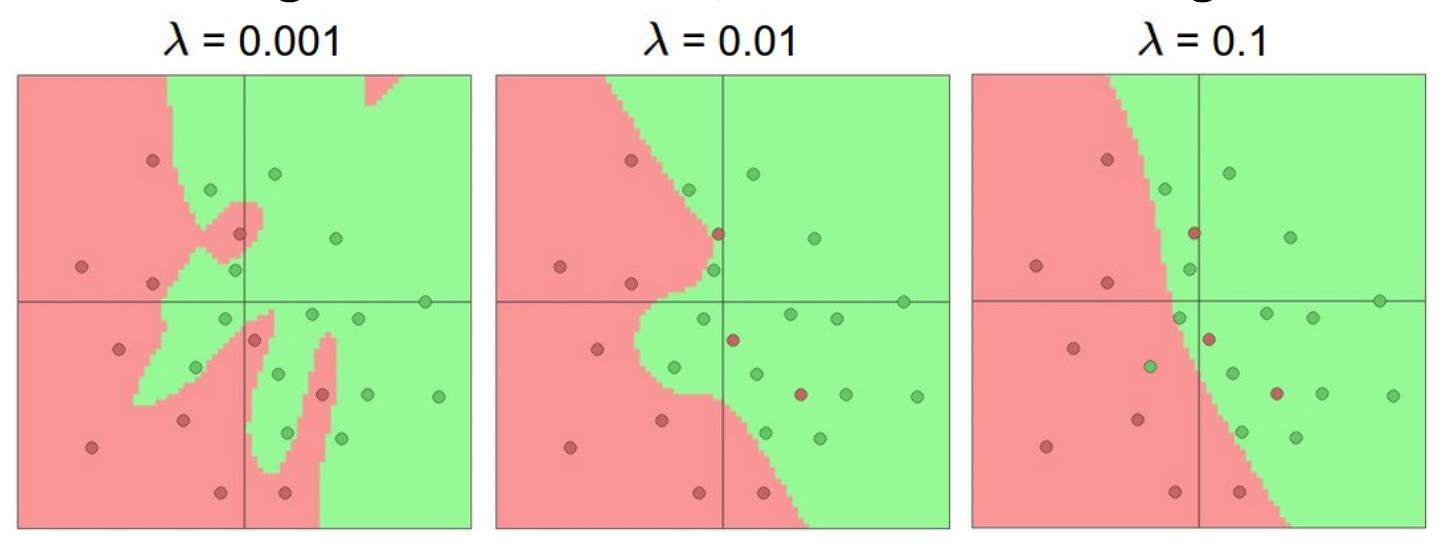
对于过拟合，我们不应该减小NN的复杂度；而是应该使用别的技术来进行regularize。

可视化demo

Universal Approximation

具有一个隐藏层的神经网络可以任意精度近似任何函数$f：R^N\to R^M$。

bump函数

对于如图的神经网络

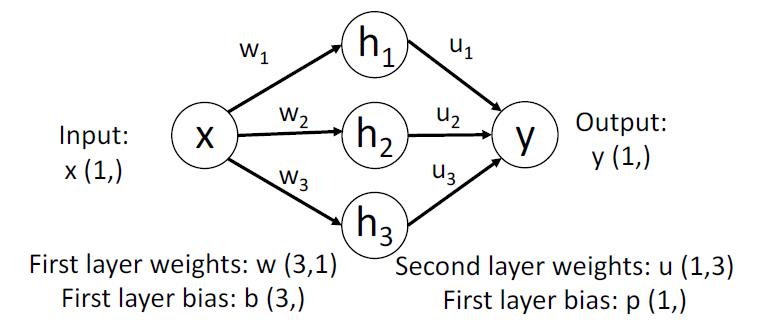
$$\begin{gathered} h1=max(0,w1\ast x+b1) \\ h2=max(0,w2\ast x+b2) \\ h3=max(0,w3\ast x+b3) \\ y=u1\ast h1+u2\ast h2+u3\ast h3+p \end{gathered}$$

对于如上的算式，如果我们有一个4单元隐层的神经网络，我们就能它来得出Bump函数

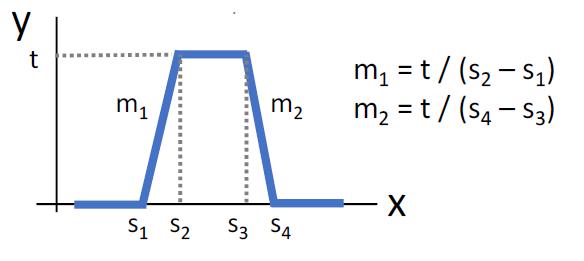
它是由4个函数叠加形成的

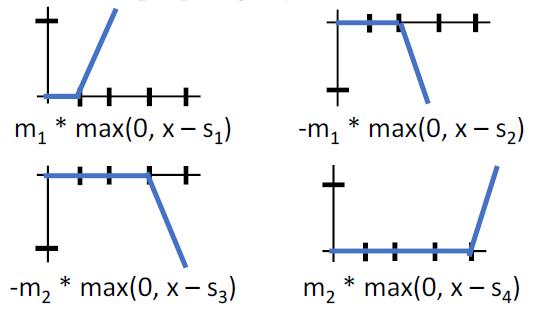
如果我们有4k个隐层单元，我们就有k个Bump函数，从而实现近似

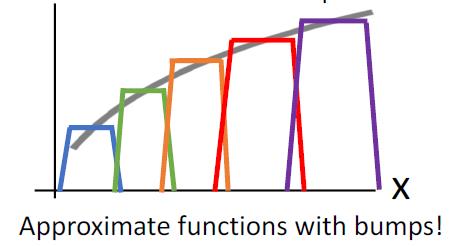
Universal approximation告诉我们：

• 神经网络可以代表任何函数

Universal approximation不能告诉我们：

• 我们是否真的可以使用SGD学习任何函数
• 学习函数需要多少数据

请记住：kNN也是Universal approximation

凸函数

凸函数的定义可以自己搜一下，百度百科的也行。

一般而言，凸函数易于优化：可以得出关于收敛到全局最小值的理论保证。而且凸函数非常适合线性分类器。

非凸函数

大多数神经网络需要非凸函数

• 很少或没有保证这个函数能收敛
• 根据经验，NN在这方面确实有效果
• 现今比较活跃的研究领域