A Probabilistic Formulation of Unsupervised Text Style Transfer

Posted 2022-12-02 Facico

A Probabilistic Formulation of Unsupervised Text Style Transfer

无监督的问题转化

设$X=x^{(1)},x^{(2)},\dots ,x^{(m)}$是领域$D_1$的数据，$Y=y^{(m+1)},y^{(m+2)},\dots ,y^{(n)}$是领域$D_2$的数据，相同的上标表示平行语句

考虑引入latent sentence将其补成平行语料库，设$\bar{X}={\bar{x}}^{(m+1)},{\bar{x}}^{(m+2)},\dots ,{\bar{x}}^{(n)}$是$D_1$的latent部分。$\bar{Y}={\bar{y}}^{(1)},{\bar{y}}^{(2)},\dots ,{\bar{y}}^{(m)}$是$D_2$的latent部分。

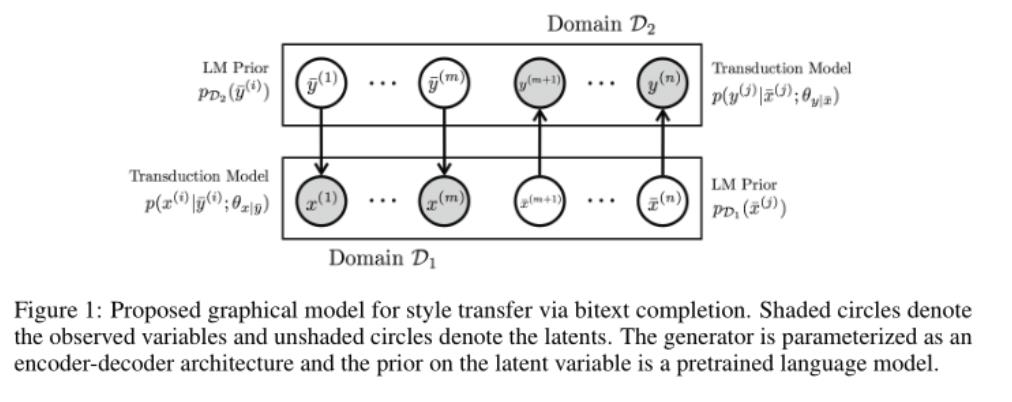
现在任务目标就变成从$X,Y$推测$\bar{X},\bar{Y}$，也就是$p(\bar{y}|x),p(\bar{x}|y)$

概率模型

直接学习$p(\bar{y}|x),p(\bar{x}|y)$是很困难的，所以改成求联合概率$p(X,Y,\bar{X},\bar{Y})$
因为我们的句子都要从latent层来生成，所以有
$$p(X,Y,\bar{X},\bar{Y})=\left(\prod _{i=1}^{m}p(x^{(i)}|{\bar{y}}^{(i)};{\theta }_{x|\bar{y}})p_{{\mathcal{D}}_2}({\bar{y}}^{(i)})\right)\left(\prod _{j=m+1}^{n}p(y^{(j)}|{\bar{x}}^{(j)};{\theta }_{y|\bar{x}})p_{{\mathcal{D}}_1}({\bar{x}}^{(j)})\right)$$

• $p(x^{(i)}|{\bar{y}}^{(i)};{\theta }_{x|\bar{y}}),p(y^{(j)}|{\bar{x}}^{(j)};{\theta }_{y|\bar{x}})$是$D_2$到$D_1$和$D_1$到$D_2$的转换模型
• $\theta$是对应的参数
• p D 1 p_\\mathcalD_1 pD以上是关于A Probabilistic Formulation of Unsupervised Text Style Transfer的主要内容，如果未能解决你的问题，请参考以下文章

  Probabilistic SVM 与 Kernel Logistic Regression（KLR）

  论文阅读：《Probabilistic Neural-symbolic Models for Interpretable Visual Question Answering》

  A Probabilistic Formulation of Unsupervised Text Style Transfer

  2018 10-708 (CMU) Probabilistic Graphical Models {Lecture 21} [A Hybrid: Deep Learning and Graphical

  概率软逻辑（PSL，Probabilistic soft logic）在Groovy语言中的规则规范

  机器学习-Probabilistic interpretation