基于OpenCV实现二值图细化，骨骼化并求出端点和交叉点

Posted 晴堂

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了基于OpenCV实现二值图细化，骨骼化并求出端点和交叉点相关的知识，希望对你有一定的参考价值。

所谓细化就是经过一层层的剥离，从原来的图中去掉一些点，但仍要保持原来的形状，直到得到图像的骨架。骨架，可以理解为物体的中轴，例如一个长方形的骨架是它的长方向上的中轴线；正方形的骨架是它的中心点；圆的骨架是它的圆心，直线的骨架是它自身，孤立点的骨架也是自身。得到了骨架，就相当于突出物体的主要结构和形状信息，去除了多余信息，根据这些信息可以实现图像上特征点的检测，如端点，交叉点和拐点。

下面先介绍经典的Zhang并行快速细化算法：

        设p1点的八邻域为：

p9 p2 p3

  p8 p1 p4

p7 p6 p5

（其中p1为白点也就是物体，如果以下四个条件同时满足，则删除p1，即令p1=0）

其中迭代分为两个子过程：

过程1 细化删除条件为：              
（1）、2 <=N(p1) <= 6，   N(x)为x的8邻域中黑点的数目
（2）、A(p1)=1,A(x)指的是将p2-p8之间按序前后分别成对值为0、1的个数（背景色：0）
（3）、p2*p4*p6=0 
（4）、p4*p6*p8=0
如果同时满足以上四个条件则该点可以删除（赋值为0）。

过程2 细化删除条件为：        
（1）、2 <=N(p1) <= 6，   N(x)为x的8邻域中黑点的数目
（2）、A(p1)=1,A(x)指的是将p2-p8之间按序前后分别为0、1的对数（背景色：0）
（3）、p2*p4*p8=0 
（4）、p2*p6*p8=0
如果同时满足以上四个条件则该点可以删除。这样反复迭代，直到获取细化图像为止。

过滤部分较为简单：

如果p2+p3+p8+p9>=1,则该点可以删除（赋值为0）。实现每两个白点之间不能紧靠在一起

检测部分比较复杂需要反复实验：

过程1 确定卷积邻域范围： 

p25 p10 p11 p12 p13

p24 p9 p2 p3 p14

  p23 p8 p1 p4 p15

p22 p7 p6 p5 p16

p21 p20 p19 p18 p17

（这里是使用5x5，实际上为了更好的检测需要至少6x6的卷积且为圆形）

过程2 统计卷积范围内白点个数：

如果白点个数较多，则说明p1为交叉点。

如果白点个数较少，则说明p1为端点。

过程3 对检测出的点进行合并：

如果两个点之间距离太近，取平均值。（下面代码没有实现该功能）

所有程序源代码：

#include <opencv2/opencv.hpp>  
#include <opencv2/core/core.hpp>  
#include <iostream>  
#include <vector>  
using namespace cv;
using namespace std;

/**
* @brief 对输入图像进行细化,骨骼化
* @param src为输入图像,用cvThreshold函数处理过的8位灰度图像格式，元素中只有0与1,1代表有元素，0代表为空白
* @param maxIterations限制迭代次数，如果不进行限制，默认为-1，代表不限制迭代次数，直到获得最终结果
* @return 为对src细化后的输出图像,格式与src格式相同，元素中只有0与1,1代表有元素，0代表为空白
*/
cv::Mat thinImage(const cv::Mat & src, const int maxIterations = -1)

	assert(src.type() == CV_8UC1);
	cv::Mat dst;
	int width = src.cols;
	int height = src.rows;
	src.copyTo(dst);
	int count = 0;  //记录迭代次数  
	while (true)
	
		count++;
		if (maxIterations != -1 && count > maxIterations) //限制次数并且迭代次数到达  
			break;
		std::vector<uchar *> mFlag; //用于标记需要删除的点  
		//对点标记  
		for (int i = 0; i < height; ++i)
		
			uchar * p = dst.ptr<uchar>(i);
			for (int j = 0; j < width; ++j)
			
				//如果满足四个条件，进行标记  
				//  p9 p2 p3  
				//  p8 p1 p4  
				//  p7 p6 p5  
				uchar p1 = p[j];
				if (p1 != 1) continue;
				uchar p4 = (j == width - 1) ? 0 : *(p + j + 1);
				uchar p8 = (j == 0) ? 0 : *(p + j - 1);
				uchar p2 = (i == 0) ? 0 : *(p - dst.step + j);
				uchar p3 = (i == 0 || j == width - 1) ? 0 : *(p - dst.step + j + 1);
				uchar p9 = (i == 0 || j == 0) ? 0 : *(p - dst.step + j - 1);
				uchar p6 = (i == height - 1) ? 0 : *(p + dst.step + j);
				uchar p5 = (i == height - 1 || j == width - 1) ? 0 : *(p + dst.step + j + 1);
				uchar p7 = (i == height - 1 || j == 0) ? 0 : *(p + dst.step + j - 1);
				if ((p2 + p3 + p4 + p5 + p6 + p7 + p8 + p9) >= 2 && (p2 + p3 + p4 + p5 + p6 + p7 + p8 + p9) <= 6)
				
					int ap = 0;
					if (p2 == 0 && p3 == 1) ++ap;
					if (p3 == 0 && p4 == 1) ++ap;
					if (p4 == 0 && p5 == 1) ++ap;
					if (p5 == 0 && p6 == 1) ++ap;
					if (p6 == 0 && p7 == 1) ++ap;
					if (p7 == 0 && p8 == 1) ++ap;
					if (p8 == 0 && p9 == 1) ++ap;
					if (p9 == 0 && p2 == 1) ++ap;

					if (ap == 1 && p2 * p4 * p6 == 0 && p4 * p6 * p8 == 0)
					
						//标记  
						mFlag.push_back(p + j);
					
				
			
		

		//将标记的点删除  
		for (std::vector<uchar *>::iterator i = mFlag.begin(); i != mFlag.end(); ++i)
		
			**i = 0;
		

		//直到没有点满足，算法结束  
		if (mFlag.empty())
		
			break;
		
		else
		
			mFlag.clear();//将mFlag清空  
		

		//对点标记  
		for (int i = 0; i < height; ++i)
		
			uchar * p = dst.ptr<uchar>(i);
			for (int j = 0; j < width; ++j)
			
				//如果满足四个条件，进行标记  
				//  p9 p2 p3  
				//  p8 p1 p4  
				//  p7 p6 p5  
				uchar p1 = p[j];
				if (p1 != 1) continue;
				uchar p4 = (j == width - 1) ? 0 : *(p + j + 1);
				uchar p8 = (j == 0) ? 0 : *(p + j - 1);
				uchar p2 = (i == 0) ? 0 : *(p - dst.step + j);
				uchar p3 = (i == 0 || j == width - 1) ? 0 : *(p - dst.step + j + 1);
				uchar p9 = (i == 0 || j == 0) ? 0 : *(p - dst.step + j - 1);
				uchar p6 = (i == height - 1) ? 0 : *(p + dst.step + j);
				uchar p5 = (i == height - 1 || j == width - 1) ? 0 : *(p + dst.step + j + 1);
				uchar p7 = (i == height - 1 || j == 0) ? 0 : *(p + dst.step + j - 1);

				if ((p2 + p3 + p4 + p5 + p6 + p7 + p8 + p9) >= 2 && (p2 + p3 + p4 + p5 + p6 + p7 + p8 + p9) <= 6)
				
					int ap = 0;
					if (p2 == 0 && p3 == 1) ++ap;
					if (p3 == 0 && p4 == 1) ++ap;
					if (p4 == 0 && p5 == 1) ++ap;
					if (p5 == 0 && p6 == 1) ++ap;
					if (p6 == 0 && p7 == 1) ++ap;
					if (p7 == 0 && p8 == 1) ++ap;
					if (p8 == 0 && p9 == 1) ++ap;
					if (p9 == 0 && p2 == 1) ++ap;

					if (ap == 1 && p2 * p4 * p8 == 0 && p2 * p6 * p8 == 0)
					
						//标记  
						mFlag.push_back(p + j);
					
				
			
		

		//将标记的点删除  
		for (std::vector<uchar *>::iterator i = mFlag.begin(); i != mFlag.end(); ++i)
		
			**i = 0;
		

		//直到没有点满足，算法结束  
		if (mFlag.empty())
		
			break;
		
		else
		
			mFlag.clear();//将mFlag清空  
		
	
	return dst;


/**
* @brief 对骨骼化图数据进行过滤，实现两个点之间至少隔一个空白像素
* @param thinSrc为输入的骨骼化图像,8位灰度图像格式，元素中只有0与1,1代表有元素，0代表为空白
*/
void filterOver(cv::Mat thinSrc)

	assert(thinSrc.type() == CV_8UC1);
	int width = thinSrc.cols;
	int height = thinSrc.rows;
	for (int i = 0; i < height; ++i)
	
		uchar * p = thinSrc.ptr<uchar>(i);
		for (int j = 0; j < width; ++j)
		
			// 实现两个点之间至少隔一个像素
			//  p9 p2 p3  
			//  p8 p1 p4  
			//  p7 p6 p5  
			uchar p1 = p[j];
			if (p1 != 1) continue;
			uchar p4 = (j == width - 1) ? 0 : *(p + j + 1);
			uchar p8 = (j == 0) ? 0 : *(p + j - 1);
			uchar p2 = (i == 0) ? 0 : *(p - thinSrc.step + j);
			uchar p3 = (i == 0 || j == width - 1) ? 0 : *(p - thinSrc.step + j + 1);
			uchar p9 = (i == 0 || j == 0) ? 0 : *(p - thinSrc.step + j - 1);
			uchar p6 = (i == height - 1) ? 0 : *(p + thinSrc.step + j);
			uchar p5 = (i == height - 1 || j == width - 1) ? 0 : *(p + thinSrc.step + j + 1);
			uchar p7 = (i == height - 1 || j == 0) ? 0 : *(p + thinSrc.step + j - 1);
			if (p2 + p3 + p8 + p9 >= 1)
			
				p[j] = 0;
			
		
	


/**
* @brief 从过滤后的骨骼化图像中寻找端点和交叉点
* @param thinSrc为输入的过滤后骨骼化图像,8位灰度图像格式，元素中只有0与1,1代表有元素，0代表为空白
* @param raudis卷积半径，以当前像素点位圆心，在圆范围内判断点是否为端点或交叉点
* @param thresholdMax交叉点阈值，大于这个值为交叉点
* @param thresholdMin端点阈值，小于这个值为端点
* @return 为对src细化后的输出图像,格式与src格式相同，元素中只有0与1,1代表有元素，0代表为空白
*/
std::vector<cv::Point> getPoints(const cv::Mat &thinSrc, unsigned int raudis = 4, unsigned int thresholdMax = 6, unsigned int thresholdMin = 4)

	assert(thinSrc.type() == CV_8UC1);
	int width = thinSrc.cols;
	int height = thinSrc.rows;
	cv::Mat tmp;
	thinSrc.copyTo(tmp);
	std::vector<cv::Point> points;
	for (int i = 0; i < height; ++i)
	
		for (int j = 0; j < width; ++j)
		
			if (*(tmp.data + tmp.step * i + j) == 0)
			
				continue;
			
			int count=0;
			for (int k = i - raudis; k < i + raudis+1; k++)
			
				for (int l = j - raudis; l < j + raudis+1; l++)
				
					if (k < 0 || l < 0||k>height-1||l>width-1)
					
						continue;
						
					
					else if (*(tmp.data + tmp.step * k + l) == 1)
					
						count++;
					
				
			

			if (count > thresholdMax||count<thresholdMin)
			
				Point point(j, i);
				points.push_back(point);
			
		
	
	return points;



int main(int argc, char*argv[])

	cv::Mat src;
	//获取图像  
	if (argc != 2)
	
		src = cv::imread("src.jpg", cv::IMREAD_GRAYSCALE);
	
	else
	
		src = cv::imread(argv[1], cv::IMREAD_GRAYSCALE);
	
	if (src.empty())
	
		std::cout << "读取文件失败！" << std::endl;
		return -1;
	

	//将原图像转换为二值图像  
	cv::threshold(src, src, 128, 1, cv::THRESH_BINARY);
	//图像细化，骨骼化  
	cv::Mat dst = thinImage(src);
	//过滤细化后的图像
	filterOver(dst);
	//查找端点和交叉点  
	std::vector<cv::Point> points = getPoints(dst,6,9,6);
	//二值图转化成灰度图，并绘制找到的点
	dst = dst * 255;
	src = src * 255;
	vector<cv::Point>::iterator it = points.begin();
	for (;it != points.end(); it++)
	
		circle(dst, *it,4,255, 1);
	
	imwrite("dst.jpg", dst);
	//显示图像  
	cv::namedWindow("src1", CV_WINDOW_AUTOSIZE);
	cv::namedWindow("dst1", CV_WINDOW_AUTOSIZE);
	cv::imshow("src1", src);
	cv::imshow("dst1", dst);
	cv::waitKey(0);
测试结果1图片：

原图

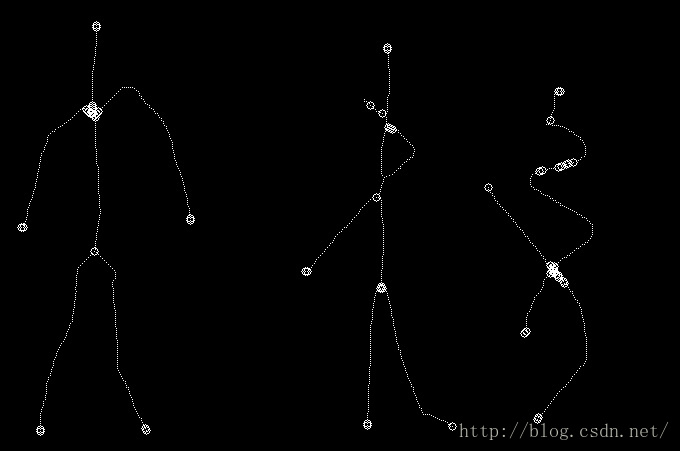
细化及检测结果

测试结果2图片：

原图

细化及检测结果

整个程序运行时间大约需要0.02秒，不会占用什么资源，代码还可以进一步优化，检测出的点也没有过滤合并。对于拐点的检测可以使用局部求导，多点拟合

或者傅里叶变换。有实现的朋友大家可以共享代码。


以上是关于基于OpenCV实现二值图细化，骨骼化并求出端点和交叉点的主要内容，如果未能解决你的问题，请参考以下文章

S0.4 二值图与阈值化

opencv统计二值图黑白像素个数

基于MATLAB的腐蚀膨胀算法实现

基于FPGA的腐蚀膨胀算法实现

OpenCV二值图求最大连通区域算法（广度优先算法 BFS）

自己写的二值图的轮廓图算法