Radiometry and Photometry 辐射度量学与光度学

Posted 2022-11-30 Matrix_11

Radiometry and Photometry

摄影是与我们周围环境的光影打交道的，但是因为人眼的特殊构造，或者说大自然的奇妙，让人眼对不同波长的光的敏感度是不同的，不仅是人类，不同生物的视觉系统，对不同波长的光谱都有一定的选择性，所以我们衡量周围环境的光线的时候，有两个不同的度量体系，一个是 Radiometry，另外一个是 Photometry，Radiometry 表示的是环境中光线的实际能量，而 Photometry 表示的是人眼感受到的环境光线的能量。

很多生物的视觉系统，包括人眼在内，都可以看成类似一个带通滤波器，对某些特定波长的光线更加敏感，人眼对于光谱中不同波长的响应是不同的，这个响应可以理解成是一个实际光线的能量与人眼感受到的光线能量的转换，国际上定义这个转换为 Luminous efficiency （$\Phi (\lambda )$）, 实验发现人眼对波长为 555nm 的光最为敏感，所以用这个波长的数据作为相对数值的标准，即 $v(\lambda )=1$，其它波长的敏感度都是小于 1 的数值，离 555nm 越远，敏感度越低，所以人眼一般能够感受的就是我们常说的可见光波段的光线，超过这个波段的，人眼基本感受不到。人眼的敏感度与不同波长的光线的关系如下图所示：

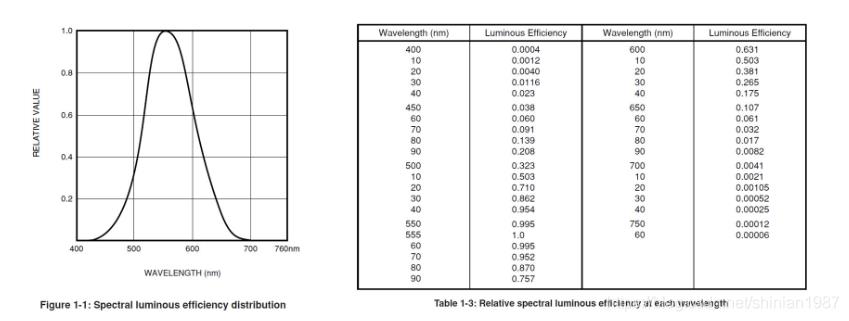
光通量–流明 lm

流明是光度学（Photometry）上类比于"功率"的概念，和辐射度量学上的瓦特（W）是可以进行对应并进行理解的，光源所发出的光能是向所有方向辐射的，对于在单位时间里通过某一面积的光能，称为通过这一面积的辐射能通量，在人眼最灵敏的555nm处，流明(lm)和瓦特（W）的换算关系常数$K_m$=638lm/W。或者说，真实的功率（Φe）为1瓦的555nm的光，其光通量（Φ）为638流明

而对于其他波长，由于人眼不那么灵敏，同样功率为1W的光，其光通量（Φ）是达不到638lm的；或者说同样1W的光，我们会觉得其他颜色的光不及555nm的亮，luminous efficiency（$v(\lambda )$）越小，我们会觉得这光越弱。对于任意波长 $\lambda$，如果其功率是 ${\Phi }_e(\lambda )$，那么在光度学（photometry）上的光通量$\Phi (\lambda )$为：

$$\Phi (\lambda )=K_m\cdot {\Phi }_e(\lambda )\cdot v(\lambda )$$

如果是非单色光，也就是混合了不同波长的光，那么整体的光通量是需要考虑不同波长的光的：

辐射测量学（radiometry）中的功率瓦特和光度学（photometry）中的光通量流明可以如下换算：

$$\Phi =\int \Phi (\lambda )\cdot d\lambda =K_m\int {\Phi }_e(\lambda )\cdot v(\lambda )\cdot d\lambda$$

照度 Illuminance – 勒克斯 lux

勒克斯（lux）这个单位以及其对应的概念照度（illuminance），用于描述单位面积的物体/探测器受到了多少"功率"（光通量）:

$$E=\frac{d\Phi }{dS}$$

发光强度 Luminous intensity – 坎德拉（cd）

坎德拉（cd）这个单位以及其对应的概念发光强度（Luminous intensity），被用于描述在人眼看来，一个点光源究竟亮不亮，以点光源为原点的单位立体角（单位为球面度sr）内总共有多大的"功率"。其在辐射测量学上对应的单位是：W/sr（瓦特每球面度）。

$$I=\frac{d\Phi }{dw}$$

发光亮度 Luminance – 坎德拉 $cd/m^2$

除了点光源，面光源也非常常见。所以另有一个发光亮度的概念来描述面光源的强度。而对于面光源，观察者和这个面所呈的角度也很重要，所以在发光强度的基础上除了需要考虑面积，还得考虑面与观察者的角度问题。

$$M=\frac{dI}{ds\cdot cos\theta }$$

参考文献：

http://share.hamamatsu.com.cn/specialDetail/838.html