编译原理笔记--语法分析

Posted 2022-11-30 FANCY PANDA

自顶向下的分析

从分析树的顶部向底部方向构造分析树
例子：

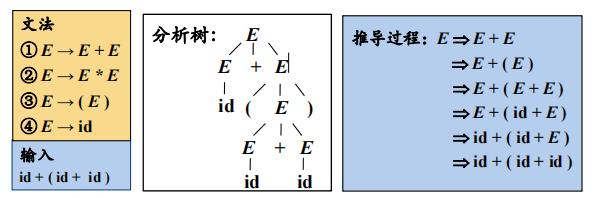
最左推导
总是选择每个句型的最左非终结符进行替换
例子：

最右推导
总是选择每个句型的最右非终结符进行替换
例子：

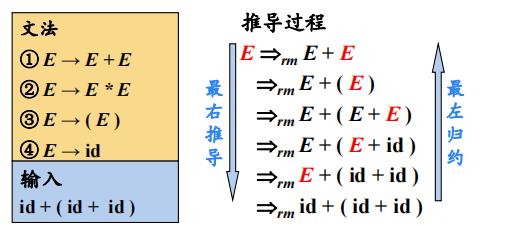
自顶向下的语法分析采用最左推导方式
例子：

文法转换

消除直接左递归

A → Aα | β(α≠ ε, β不以A开头)
A → β A′
A′ → α A′｜ε

例子：

一般形式

消除间接左递归

非终结符的后继符号集

• 非终结符A的后继符号集
• 可能在某个句型中紧跟在A后边的终结符a的集合，记为FOLLOW(A)
• FOLLOW(A)=a| S ⇒* αAaβ, a∈VT，α,β∈(VT∪VN)*
  

产生式的可选集

• 产生式A→β的可选集是指可以选用该产生式进行推导时对应的输入符号的集合，记为SELECT( A→β )
• SELECT( A→aβ ) = a
• SELECT( A→ε )=FOLLOW( A )

串首终结符集
串首第一个符号，并且是终结符
给定一个文法符号串α， α的串首终结符集FIRST(α)被定义为可以从α推导出的所有串首终结符构成的集合。如果α ⇒* ε，那么ε也在FIRST(α)中

• ∀α∈(VT∪V N)+, FIRST(α)= a | α ⇒* aβ，a∈ VT，β∈(V T∪ V N)*；
• 如果 α ⇒* ε，那么 ε∈FIRST(α)

产生式A→α的可选集SELECT

• 如果 ε∉FIRST(α), 那么SELECT(A→α)= FIRST(α)
• 如果 ε∈FIRST(α), 那么SELECT(A→α)=( FIRST(α)-ε )∪FOLLOW(A)

LL(1)文法
当且仅当G的任意两个具有相同左部的产生式A → α | β 满足下面的条件：

• 如果α 和β均不能推导出ε ，则FIRST (α)∩FIRST (β) =Φ
• α 和β至多有一个能推导出ε
• 如果 β ⇒* ε，则FIRST (α)∩FOLLOW(A) =Φ；
• 如果 α ⇒* ε，则FIRST (β)∩FOLLOW(A) =Φ；

FIRST集和FOLLOW集的计算

计算文法符号X的FIRST(X )

• FIRST ( X )：可以从X推导出的所有串首终结符构成的集合
• 如果 X ⇒* ε，那么 ε∈FIRST ( X )
  
  算法
• 不断应用下列规则，直到没有新的终结符或ε可以被加入到任何FIRST集合中为止
• 如果X是一个终结符，那么FIRST ( X ) = X
• 如果X是一个非终结符，且 X→Y1…Yk∈P (k≥1)，那么如果对于某个i，a在FIRST (Yi ) 中且ε 在所有的FIRST(Y1) , … , FIRST(Yi-1)中(即Y1…Yi-1 * ε )，就把a加入到FIRST( X )中。如果对于所有的 j = 1,2, . . . , k，ε在FIRST(Yj)中，那么将ε加入到FIRST( X )
• 如果 X→ε∈P，那么将ε加入到FIRST( X )中

计算串X1X2 …Xn的FIRST 集合

• 向FIRST(X1X2…Xn)加入FIRST(X1)中所有的非ε符号
• 如果ε在FIRST(X1)中，再加入FIRST(X2)中的所有非ε符号；
• 如果ε在FIRST(X1)和FIRST(X2)中，再加入FIRST(X3)中的所有非ε符号，以此类推
• 最后，如果对所有的i，ε都在FIRST(Xi)中，那么将ε加入到FIRST(X1X2…Xn) 中

计算非终结符A的FOLLOW(A)

• FOLLOW(A)：可能在某个句型中紧跟在A后边的终结符a的集合
• FOLLOW(A)=a| S ⇒* αAaβ, a∈VT，α,β∈(VT∪VN)*
• 如果A是某个句型的的最右符号，则将结束符“$”添加到FOLLOW(A)中

例子：

算法

• 不断应用下列规则，直到没有新的终结符可以被加入到任何FOLLOW集合中为止
• 将 $ 放入FOLLOW( S )中，其中S是开始符号，$是输入右端的结束标记
• 如果存在一个产生式A→αBβ，那么FIRST ( β )中除ε 之外的所有符号都在FOLLOW( B )中
• 如果存在一个产生式A→αB，或存在产生式A→αBβ且FIRST ( β ) 包含ε，那么 FOLLOW( A )中的所有符号都在FOLLOW( B )中
  例：
  表达式文法各产生式的SELECT 集
  
  
  

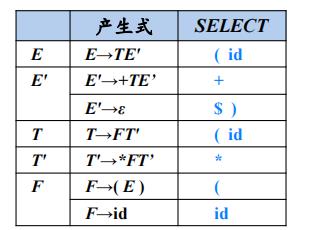
自底向上的语法分析

• 从分析树的底部(叶节点)向顶部(根节点)方向构造分析树
• 可以看成是将输入串w归约为文法开始符号S的过程
• 自顶向下的语法分析采用最左推导方式
• 自底向上的语法分析采用最左归约方式（反向构造最右推导）
• 自底向上语法分析的通用框架

例：
移入-归约分析

• 移入：将下一个输入符号移到栈的顶端
• 归约：被归约的符号串的右端必然处于栈顶。语法分析器在栈中确定这个串的左端，并决定用哪个非终结符来替换这个串
• 接收：宣布语法分析过程成功完成
• 报错：发现一个语法错误，并调用错误恢复子例程

LR分析法概述

• L: 对输入进行从左到右的扫描
• R: 反向构造出一个最右推导序列
• LR(k)分析需要向前查看k个输入符号的LR分析

LR(0) 项目

右部某位置标有圆点的产生式称为相应文法的一个LR(0)项目（简称为项目）
A→ α1·α2

LR(0)自动机

LR(0) 自动机的形式化定义
文法
G = ( VN , VT , P , S )
LR(0)自动机
M = ( C, VN∪VT , GOTO, Io , F )
C=Io∪I | J∈C, X∈VN∪VT, I=GOTO(J,X )
Io=CLOSURE(S′ →.S )
F= CLOSURE(S′ →S.)
LR(0) 分析过程中的冲突


例子：
移进/归约冲突和归约/归约冲突

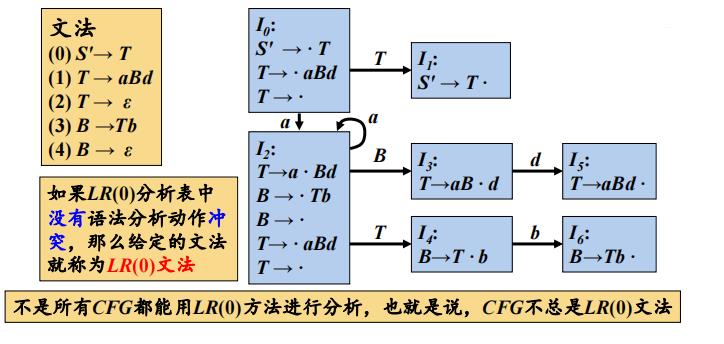
LR(1)分析
对于产生式 A→α的归约，在不同的使用位置， A会要求不同的后继符号

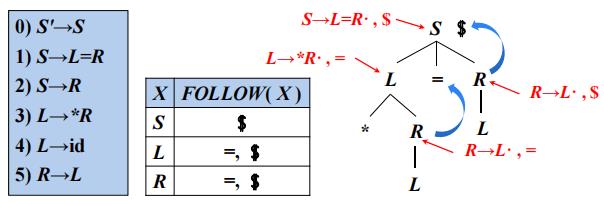
将一般形式为 [A→α·β, a]的项称为 LR(1) 项，其中A→αβ 是一个产生式，a 是一个终结符(这里将$视为一个特殊的终结符)它表示在当前状态下，A后面必须紧跟的终结符，称为该项的展望符
LR(1) 中的1指的是项的第二个分量的长度

• 在形如[A→α·β, a]且β ≠ ε的项中，展望符a没有任何作用
• 但是一个形如[A→α·, a]的项在只有在下一个输入符号等于a时才可以按照A→α 进行归约
• 这样的a的集合总是FOLLOW(A)的子集，而且它通常是一个真子集

例子：
LR(1)自动机

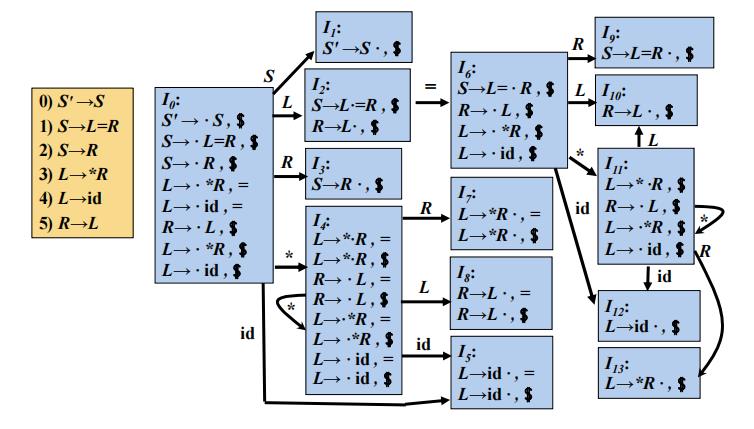
赋值语句文法的
LR(1)分析表

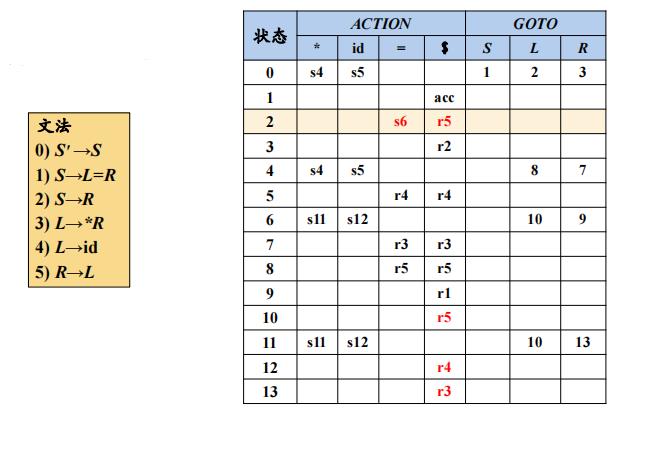
LR(1)自动机的形式化定义
文法
G = (VN , VT , P, S )
LR(1)自动机
M = (C, VN∪VT , GOTO, Io , F )
C=Io∪I | J∈C, X∈VN∪VT, I=GOTO(J,X )
Io=CLOSURE(S’ →·S, $)
F= CLOSURE(S’→S· , $)