线性回归（百米赛跑python）

Posted 2022-11-27 木头科技㉿

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

x = [1940,1960,1980,2000,2020] #年份，顺序为1940，1960，1980，2000，2020
x = np.reshape(x,newshape=(5,1)) / 1000.0
y =  [21332, 20162, 19138, 18621, 18016] #百米赛跑需要的时间，单位为毫秒
y = np.reshape(y,newshape=(5,1)) / 10000.0

plt.scatter(x,y) #先绘制散点图

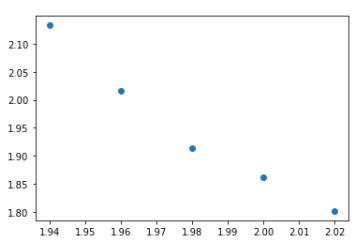
数据分析 Data Analysis

看样子像一条直线

算法采用 Algorithm

模型 Model
损失函数 Cost Function
优化方法 Optimization Method
模型 -> 损失函数 -> 优化方法

def model(a, b, x):
    return a*x + b #预测模型表达式

def cost_function(a, b, x, y):
    n = 5
    return 0.5/n * (np.square(y-a*x-b)).sum() #代价函数的计算

def optimize(a,b,x,y):
    n = 5
    alpha = 1e-1
    y_hat = model(a,b,x)
    da = (1.0/n) * ((y_hat-y)*x).sum() #梯度下降法
    db = (1.0/n) * ((y_hat-y).sum()) #梯度下降法
    a = a - alpha*da
    b = b - alpha*db
    return a, b

初始化

a = 0
b = 0

第一次遍历

def iterate(a,b,x,y,times):
    for i in range(times):
        a,b = optimize(a,b,x,y)

    y_hat=model(a,b,x)
    cost = cost_function(a, b, x, y)
    print (a,b,cost)
    plt.scatter(x,y)
    plt.plot(x,y_hat)
    return a,b

a,b = iterate(a,b,x,y,1)

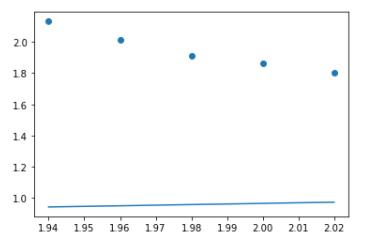
继续遍历

a,b = iterate(a,b,x,y,5)

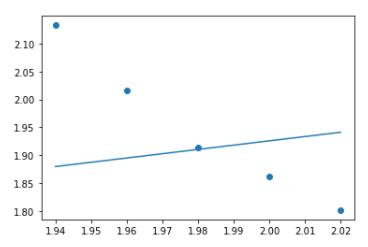
a,b = iterate(a,b,x,y,10)

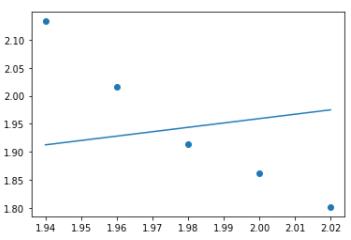
a,b = iterate(a,b,x,y,100)

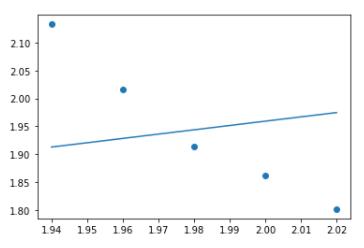
a,b = iterate(a,b,x,y,10000) #迭代10000次

a,b = iterate(a,b,x,y,90000) #迭代90000次，发现拟合效果比较好

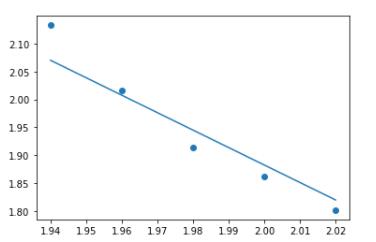
模型评价

计算R平方

y_hat=model(a,b,x)
y_bar = y.mean()
SST = np.square(y - y_bar).sum()
SSR = np.square(y_hat - y_bar).sum()
SSE = np.square(y_hat - y).sum()
SST, SSR, SSE

y_hat

y_hat-y

证明 SST=SSR+SSE

error = SST - SSR -SSE
error

R_Square = SSR/SST
R_Square