堆的创建与删除

Posted 2022-11-26 语风之

目录

一、堆的介绍

二、函数分析

1.创建小堆

2.堆的删除

3.堆的插入

4.堆排序 

4.TOP-K问题

三、完整源码与小结

1.完整源码

2.小结

---

一、堆的介绍

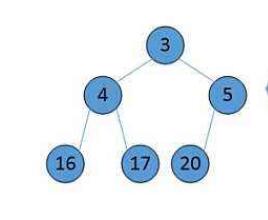
如果有一个关键码的集合K=k0,k1,k2,k3,......k(n-1),把所有的元素按照完全二叉树的顺序存储方式存储在一个一维数组中，并满足：Ki<=K(i*2+1)且Ki<=K(i*2+2)（  或Ki>=K(i*2+1)且Ki>=K(i*2+2)  ）,i=0,1,2,......,则称为小堆（或大堆）。
将根节点最大的堆称为最大堆，将根节点最小的堆称为最小堆。

小堆

二、函数分析

1.创建小堆

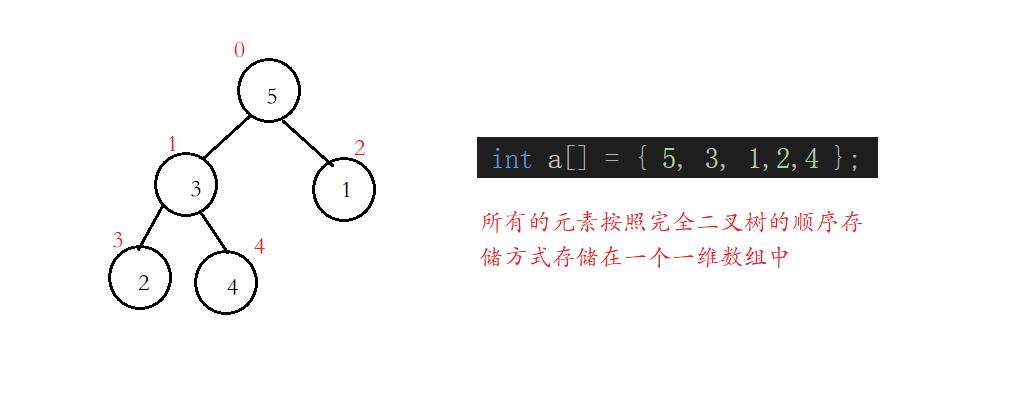
如图所示，已知一维数组a，a中存储着元素5,3,1,2,4,左侧二叉树为数组对应的完全二叉树。我们将根据向下调整法，从倒数第一个非叶子节点root开始调整，一直调整到根节点，就可以调整成小堆。

tip：

倒数第一个非叶子节点root与节点个数size的关系为：root=size/2-1,所以root=5/2-1=1。

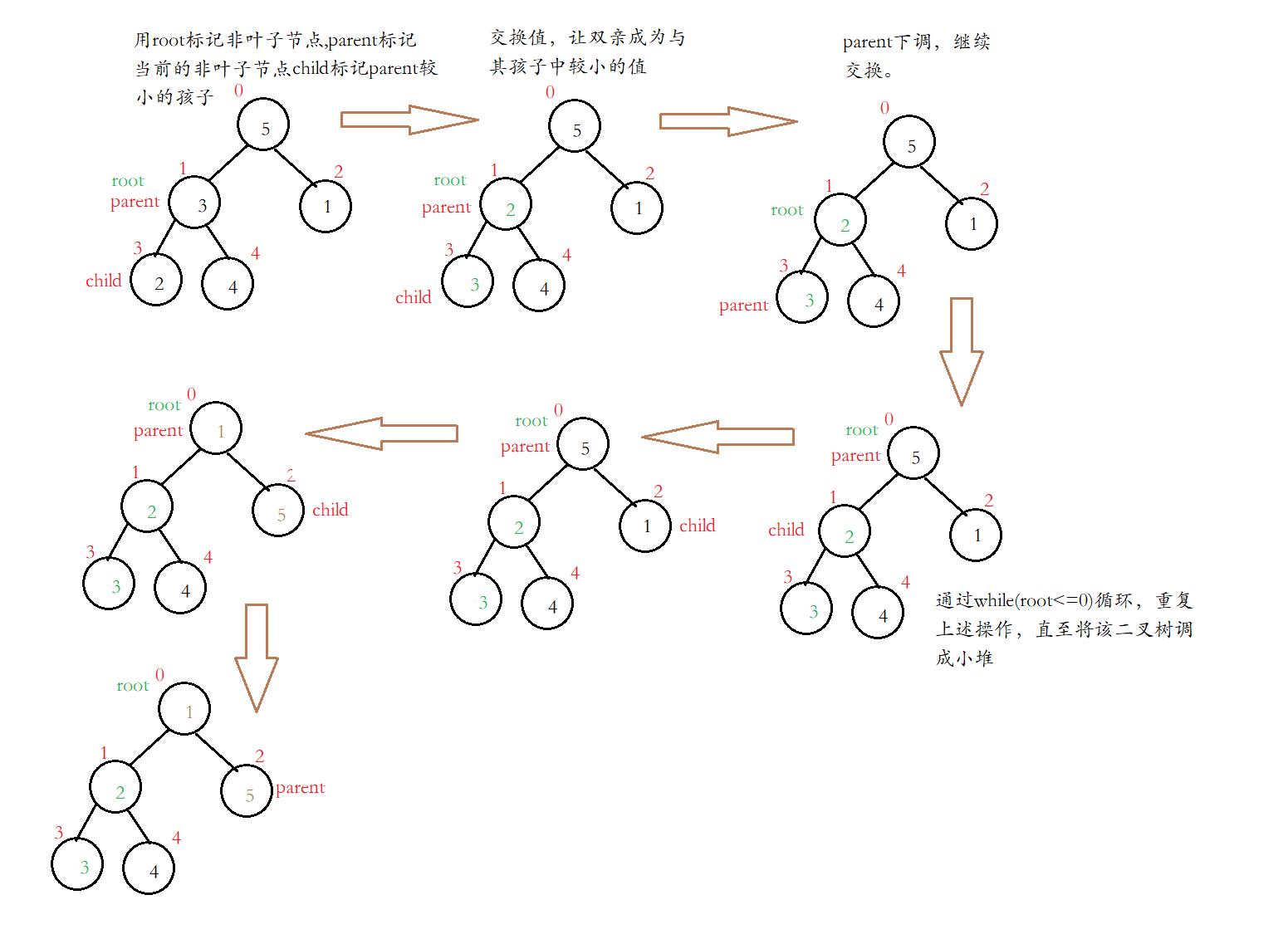
（用root标记非叶子节点，用parent标记当前的非叶子节点，用于后续的交换）

小堆的创建（1）

（1）定义child，用child标记parent的较小的孩子。
 

int parent=root;

int child=parent*2+1;

因为完全二叉树中非叶子结点至少有一个左孩子，在不确定右孩子的情况下，先使child标记左孩子。

tip：

a.简单来说二叉树中间没有缺少结点，就是完全二叉树。

b.非叶子结点就是指有孩子结点的结点。

标记较小的孩子前注意判定条件的顺序，(child + 1 < hp->size &&hp->arry[child + 1] < hp->arry[child])。若没有右孩子，而（hp->arry[child + 1] < hp->arry[child]）写在判定条件的前面，arry[child + 1]，数组越界。

	int child = parent * 2 + 1;//此时chid表示左孩子
	//1、获取较小的孩子
	if (child + 1 < hp->size &&hp->arry[child + 1] < hp->arry[child])
    //当右孩子存在并且右孩子小于左孩子的前提下
		child = child + 1;
	

（2）交换值，让双亲成为与其孩子中较小的值

tip：

注意使用传地址交换值的方法。

		//2、使双亲的值成为双亲与孩子中更小的值
		if (hp->arry[child] < hp->arry[parent])
			Swap(&hp->arry[child], &hp->arry[parent]);
		

（3）parent下调，继续交换。

交换值以后parent结点的子树可能不满足堆的特性，所以(parent = child;)，双亲下调到孩子节点处，继续交换。

		parent = child;//交换后双亲的子树可能不满足堆的条件，因此双亲下调到孩子
		child = parent * 2 + 1;

（4）循环。

从倒数第一个非叶子节点root开始调整，一直调整到根节点，所以要使用循环，使root往前调整，直到根节点。while (child < hp->size )

创建小堆的向下调整函数：

void AdjustDown(Heap* hp,int parent)
	int child = parent * 2 + 1;//此时chid表示左孩子
	while (child < hp->size ) //循环使双亲的子树满足堆的条件
		//1、获取较小的孩子
		if (child + 1 < hp->size &&hp->arry[child + 1] < hp->arry[child])//当右孩子存在并且右孩子小于左孩子的前提下
			child = child + 1;
		
		//2、使双亲的值成为双亲与孩子中更小的值
		if (hp->arry[child] < hp->arry[parent])
			Swap(&hp->arry[child], &hp->arry[parent]);
		
		parent = child;//交换后双亲的子树可能不满足堆的条件，因此双亲下调到孩子
		child = parent * 2 + 1;
	

 函数操作图示：

创建小堆过程

2.堆的删除

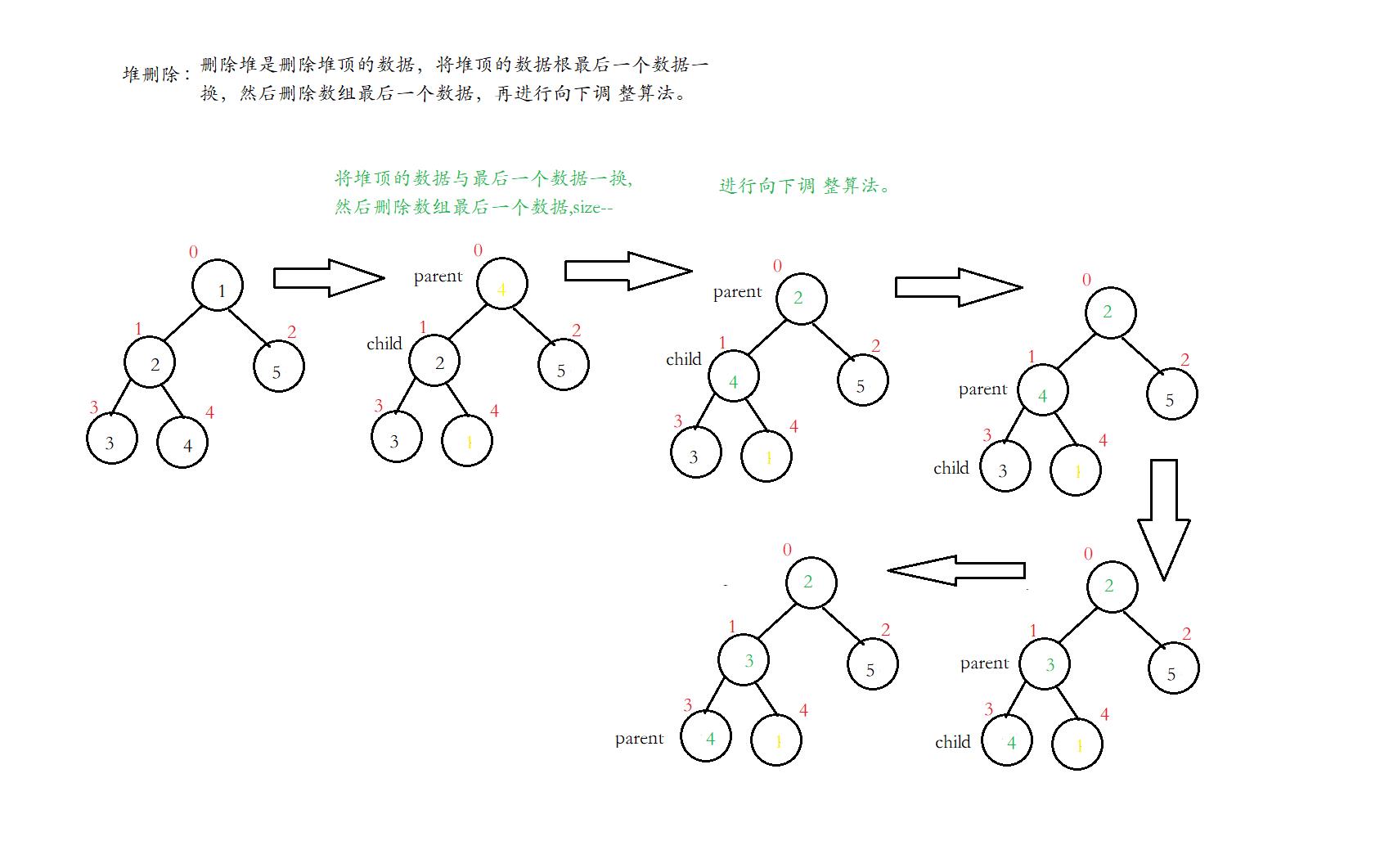
删除堆是删除堆顶的数据，将堆顶的数据与最后一个数据一换，然后删除数组最后一个数据，再进行向下调 整算法。

堆删除函数：

//堆的删除
void HeapPop(Heap* hp)
	assert(hp);
	Swap(&hp->arry[0], &hp->arry[hp->size-1]);
	hp->size--;
	AdjustDown(hp,0);

堆删除图示： 

堆删除

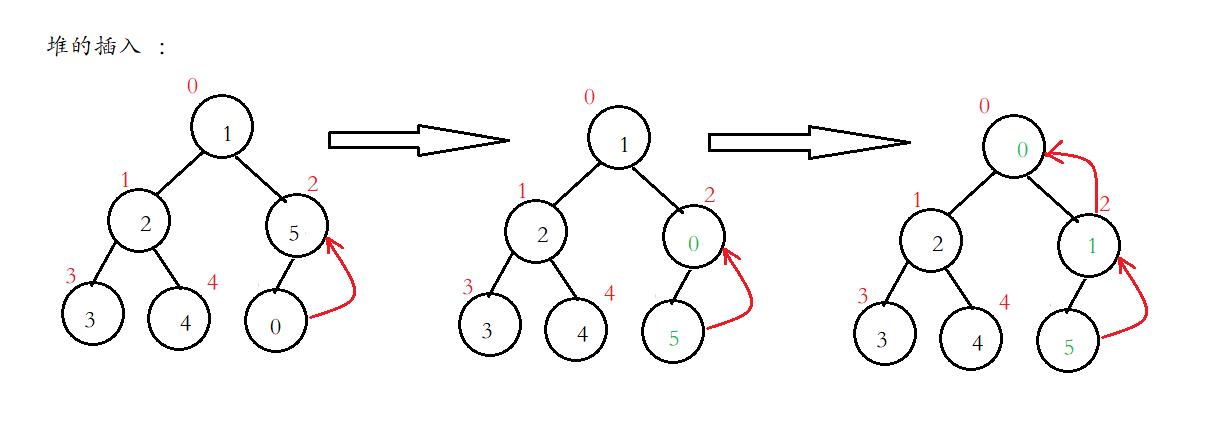
3.堆的插入

先插入一个数据到数组的尾上，再进行向上调整算法，直到满足堆。

（1）先将元素插入到堆的末尾，即最后一个孩子之后

		hp->arry[hp->size] = x;
		hp->size++;
		AdjustUp(hp);

 （2）插入之后如果堆的性质遭到破坏，将新插入的节点顺着其双亲往上调整到合适位置即可

a.标记当前插入的节点和其双亲节点

int child = hp->size - 1;

int parent = hp->size / 2 - 1

b.当child的节点的值小于其双亲节点parent的值,交换

            

Swap(&hp->arry[parent], &hp->arry[child]);

c.以parent>=0为循环的判定条件，child标记parent，parent标记此时child的非叶子节点,继续向上判定并交换，直到该二叉树满足小堆。
 

            child = parent;
            parent = child / 2 - 1;

堆的插入函数（向上调整函数）：

void AdjustUp(Heap* hp)
	int parent = hp->size / 2 - 1;//parent为堆的最后一个非叶子节点,parent与总结点数的关系为parent==size/2-1
	int child = hp->size - 1;
	while (parent >= 0)//以parent>=0为循环的判定条件，当parent==0,此时parent还可以再进行循环，当parent--，成为-1后，循环不再进行
		//1、当child的节点的值小于其双亲节点parent的值
		if (hp->arry[child] < hp->arry[parent])
			Swap(&hp->arry[parent], &hp->arry[child]);
			child = parent;
			parent = child / 2 - 1;
		
		//1、当flag的节点的值大于其双亲节点parent的值
		break;
	

 堆的插入图示：

堆插入

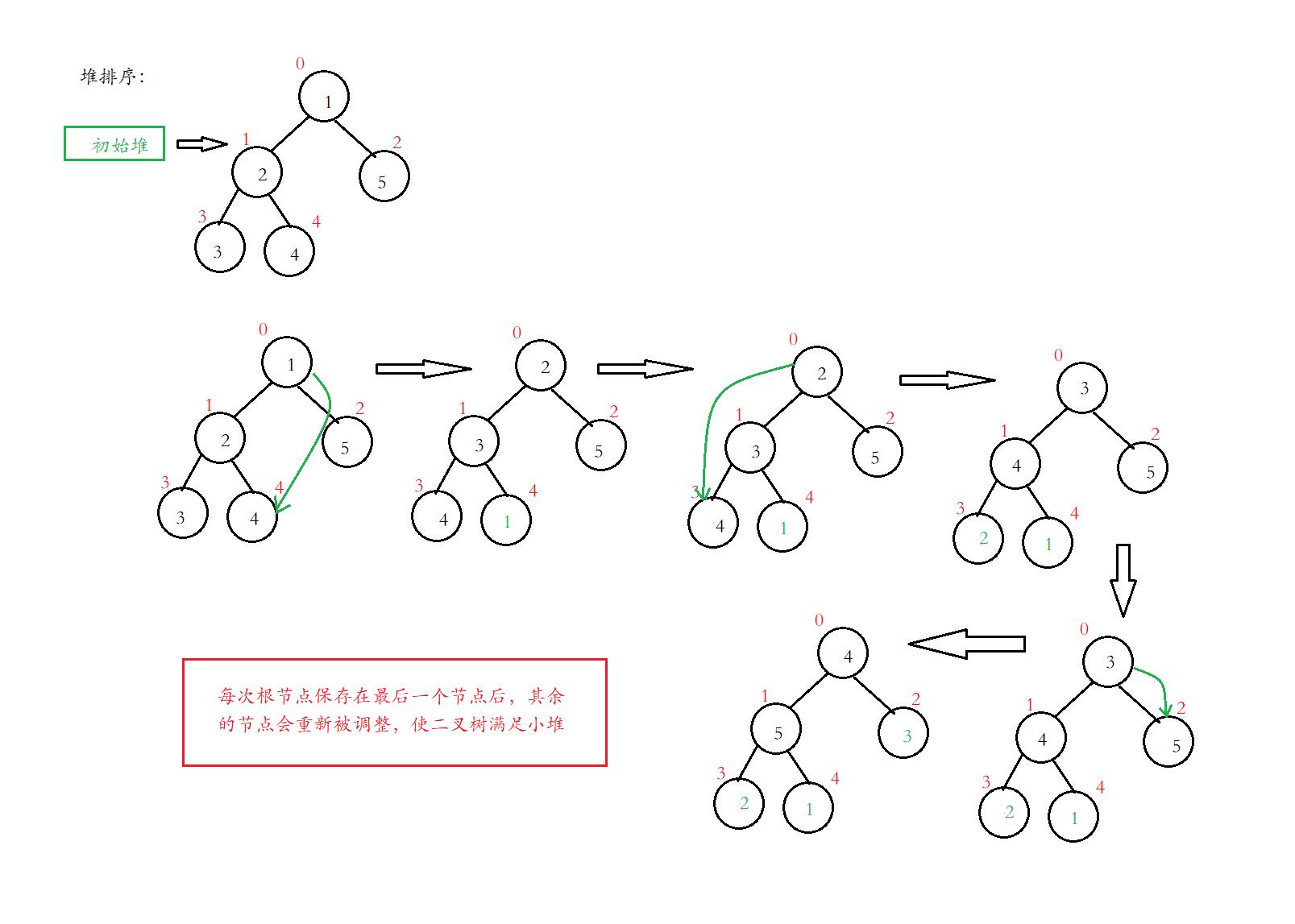
4.堆排序 

堆排序:利用堆删除的思想排序。

tip：

本次排序在小堆中获得降序排列，
（1）删除堆顶（即，将堆顶元素与最后一个元素交换）。

HeapPop(hp);//堆删除后，根节点保存在最后一个节点处

（2）除最后一个元素外，对剩下的节点从根节点开始向下调整，使二叉树满足小堆。

tip：

注意，（hp->size--）的操作在堆删除的函数中已经存在，在堆排序的函数中我们不需要再自减。

//小堆根节点保存在最后一个节点后，再对剩下的节点进行向下调整。
hp->size--;

（3）重复1、2操作（每重复一次，hp->size--），直到hp->size-->1。

tip：

若n个元素中，n-1个元素都已经完成排序，剩下的那个就不用再排序了。

while (hp->size > 1)

（4）恢复hp->size的值，hp->size=flag（flag=hp->size）

堆排序只是使用了堆删除的思想，并不是真的删除了，在完成排序后，需要恢复size的值。

	int flag = hp->size;//flag保存总的元素个数
	hp->size = flag;    //给size恢复原来的值

堆排序源码：

/*
堆排序:获得降序排列（在小堆的基础上），利用堆删除的思想排序
1、删除堆顶（即，将堆顶元素与之后一个元素交换），
2、对剩下的节点从根节点开始向下调整，使其满足小堆
3、flag=hp->size,重复1、2操作（每重复一次，hp->size--，该操作已经在堆删除中存在）直到hp->size-->1
4、恢复hp->size的值，hp->size=flag
*/
void HeapSort(Heap* hp)
	assert(hp);
	int flag = hp->size;
	while (hp->size > 1)
		HeapPop(hp);
	
	hp->size = flag;

堆排序图示： 

堆排序

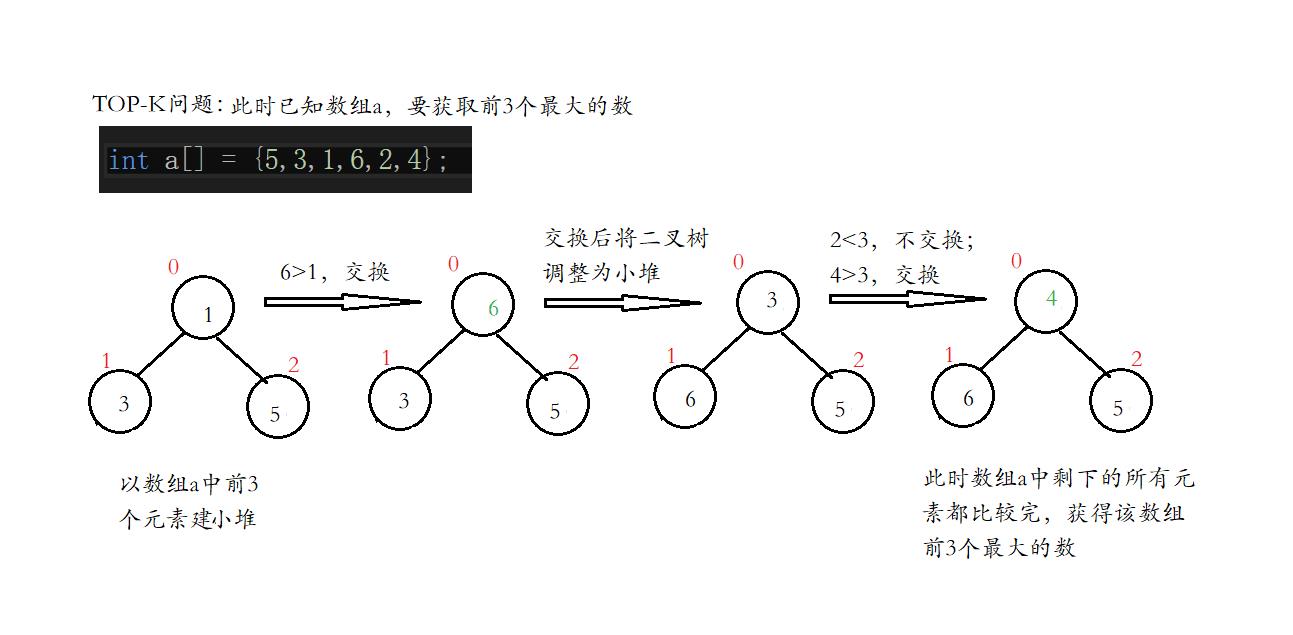
4.TOP-K问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

此处我们获取前K个最大元素 1，用数据集合前k个元素建堆。

tip：

获取前K个最大的元素就建小堆。
（1）保存数组中剩下的N-K个值的个数。

int flag=N-K;//保存数组中未建堆的数据的个数

（2）用剩下的falg个元素和堆顶一一比较，不满足则替换元素
a.若堆顶更小，则替换。替换后flag--，并从根节点开始向下调整，使二叉树满足小堆
b.重复a，直到flag==0。   

//比较的判定条件，即将数组中剩下的数比较完为止
while(flag>0)
    flag--;
 

 TOP-K问题源码：

/*
TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
此处我们获取前K个最大元素
1、
用数据集合前k个元素建堆
注意：获取前K个最大的元素就建小堆
2、
int flag=N-K;
用剩下的falg个元素和堆顶一一比较，不满足则替换元素
a.若堆顶更小，则替换。替换后flag--，并从根节点开始向下调整，使二叉树满足小堆
b.重复a，直到flag==0,即结束判定的条件为：	while(flag>0)
												flag--;
																						


void GetTopK(int* a, int n, int k)的参数介绍
a，要获取前K个最大的数据的数组，
n，数组的大小
k,要获取前K个最大的数据的数组的K的值

*/
void GetTopK(HPDataType* a, int n, int k)
	Heap* hp1 = (Heap*)malloc(sizeof(Heap));
	HeapCreate(hp1,a,k);
	int flag = n - k;
	int temp = n;
	while (flag > 0)
		if (a[n - 1] > hp1->arry[0])
			Swap(&a[n-1],&hp1->arry [0]);
		
		n--;
		AdjustDown(hp1,0);
		flag--;
	
	HeapDestory(hp1);

 TOP-K问题图示：

TOP-K问题

三、完整源码与小结

1.完整源码

点击获取源码

2.小结

在创建堆的过程中，要深刻的了解创建堆的过程与方法，总结除步骤，这样函数编写就了然于心。代码出了差错，检查不出问题，那么代码整体是没有问题的，可能只是哪个符号写错了，逐语句，逐过程执行，并打开监视窗口，逐步调试，看看在调试的过程中哪里的数据不符合预期，再分析，就能找出错误了。