矩阵基础概念之行列式与秩

Posted 2022-11-25 dqhl1990

矩阵基础概念及运算

---

1. 矩阵的线性运算

性质 1.1 设矩阵$A,B,C,D$为同型矩阵，$O$为零矩阵，$k,l$为任意常数，则有

1. $A+B=B+A$ （交换律）
2. $(A+B)+C=A+(B+C)$ （结合律）
3. $A+O=O+A=A$
4. $k(A+B)=kA+kB$
5. $(k+l)A=kA+lA$
6. $(kl)A=k(lA)$
7. $(-1)A=-A,0A=O$

2. 矩阵的乘法运算

性质 2.1 设矩阵$A,B,C$能满足相乘维度要求，$k$为常数，$E$为单位矩阵，则有

1. $(AB)C=A(BC)$
2. $A(B+C)=AB+AC$
3. $(B+C)A=BA+CA$
4. $k(AB)=(kA)B=A(kB)$
5. $E_m{A}_{m\times n}=A_{m\times n}{E}_n=A_{m\times n}$

需要注意的是，矩阵乘法与算数乘法有以下几点不同：

1. 一般的说$AB̸=BA$，即矩阵乘法不满足交换律
2. 由$AB=O$不能推出$A=O$或$B=O$，即两个非零矩阵的乘积可以是零矩阵
3. 由$AB=AC$且$A̸=O$，不能推出 $B=C$，即矩阵乘法不满足消去律

3. 矩阵的转置

性质 3.1 $k$为常数

1. $(A^T{)}^T=A$
2. $(A+B{)}^T=A^T+B^T$
3. $(kA{)}^T=k{A}^T$
4. $(AB{)}^T=B^T{A}^T$

定义 3.1 设$A$为$n$阶方阵，若$A^T=A$，则称$A$为对称阵；若$A^T=-A$，则称$A$为反对称阵。

4. 方阵的行列式

4.1 行列式计算方法

方法1 对角线规则（沙流氏规则）

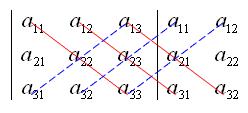
三阶矩阵的行列式为每条红线上的元素的乘积之和，减去蓝线上元素乘积之和。
$$det(A)=\left|\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right|$$