高级数据结构—斐波那契堆与二项堆详细介绍(算法导论中科大USTC)
Posted 之墨_
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了高级数据结构—斐波那契堆与二项堆详细介绍(算法导论中科大USTC)相关的知识,希望对你有一定的参考价值。

斐波那契堆与二项堆
二项堆请点击这里👈
数据结构与堆
下图列出了小顶堆在各种数据结构(链表、二叉堆、二项堆、斐波那契堆、松弛堆)的实现下,各种基本操作的时间复杂度

斐波那契堆

概述
- 斐波那契堆历史:Fredman和Tarjan(1986)
- 巧妙的数据结构和分析
- 原始动机: O ( m + n log n ) O(m+n \\log n) O(m+nlogn)最短路径算法,也导致了更快的MST算法,加权二分匹配
- 仍然领先于它的时代
- 斐波那契堆直觉:
- 类似于二项式堆,但结构不太复杂
- 减少键和联合运行时间 O ( 1 ) O(1) O(1)(均摊时间复杂度)
- “懒惰”联合
- 斐波那契堆是以斐波那契堆数命名的,用于运行时间分析。
结构
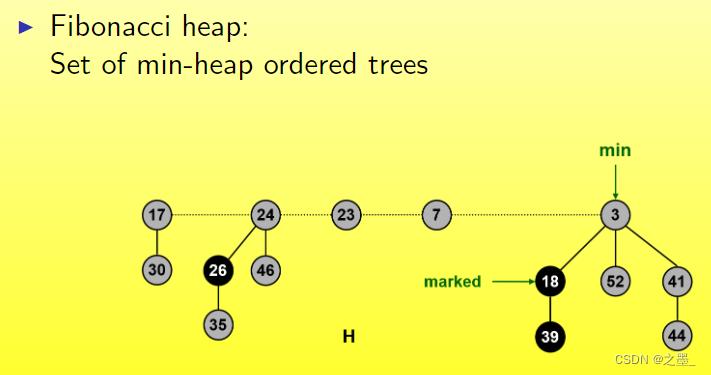
- 最小堆有序树集
实现
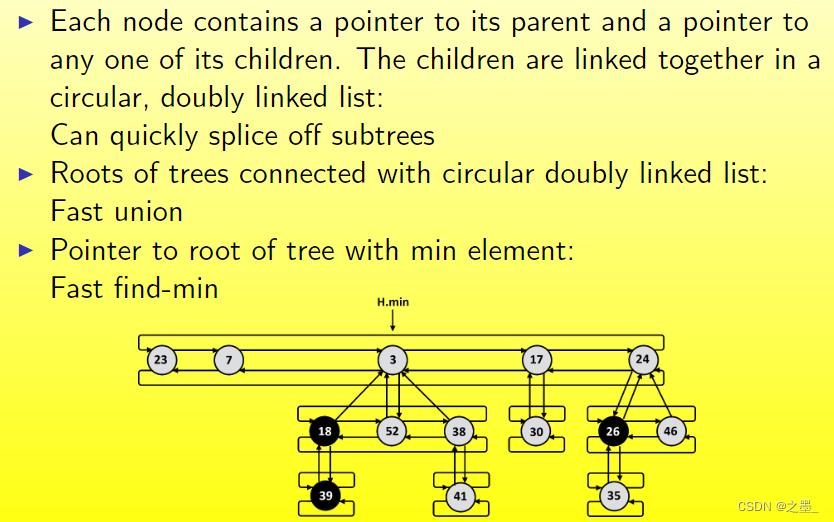
- 每个结点都有一个指向父结点的指针和指向它任意一个孩子结点的指针。孩子结点在一个循环的双链接列表中链接在一起:可以快速拼接子树
- 所有树的根在一个循环的双链接列表中链接在一起:合并操作更快
- 有一个指向最小根结点的指针:快速找到最小值结点
符号定义
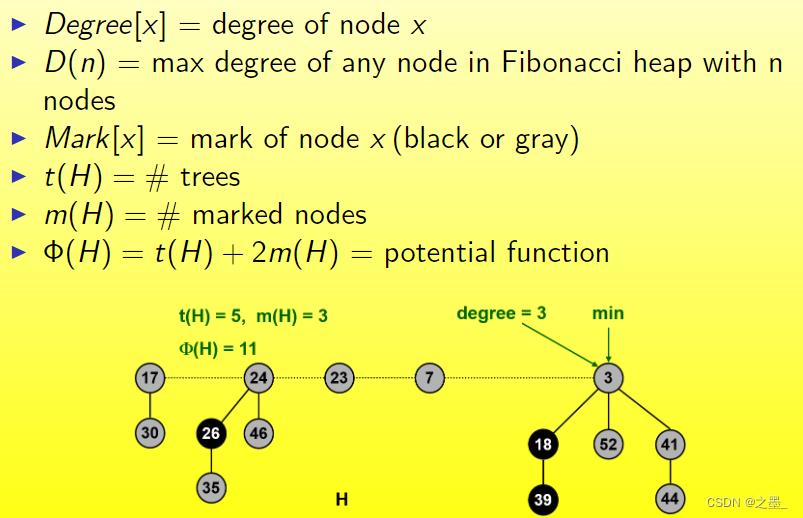
- D e g r e e [ x ] Degree[x] Degree[x] = x x x结点的度
- D ( n ) D(n) D(n) = 斐波那契堆中所有结点最大的度数
- M a r k [ x ] Mark[x] Mark[x] = 结点 x x x的标记(黑色或灰色)
- t ( H ) t(H) t(H) = H H H根链表中树的数目
- m ( H ) m(H) m(H) = H H H中已标记的结点数目
- Φ ( H ) \\Phi(H) Φ(H) = t ( H ) + 2 m ( H ) t(H) + 2m(H) t(H)+2m(H)= 斐波那契堆的势函数
插入结点
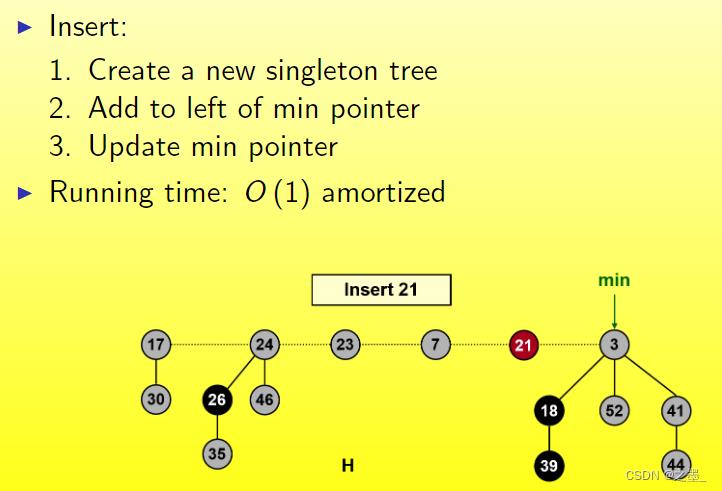
- 创建一个新的单例树
- 添加到最小指针的左侧
- 更新最小指针
- 时间复杂度: O ( 1 ) O(1) O(1)
合并

- 连接两个斐波那契堆
- 根列表是循环的双链表
- 连接两个根链,更新最小值结点
- 摊还时间复杂度为 O ( 1 ) O(1) O(1)
示例
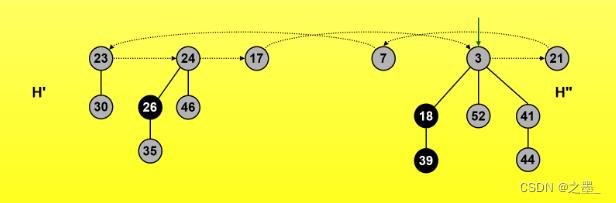
抽取最小结点

- 删除最小结点并把它的孩子结点链入根链
- 合并根链中相同度数的树
示例
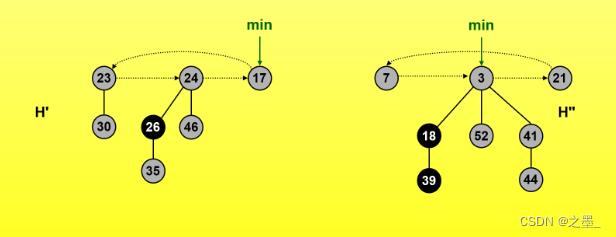
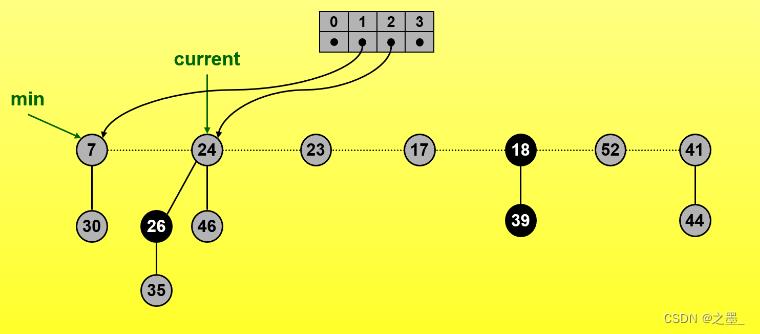
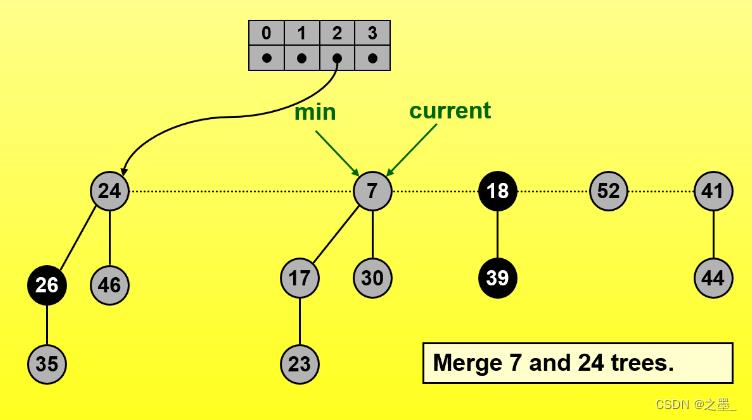
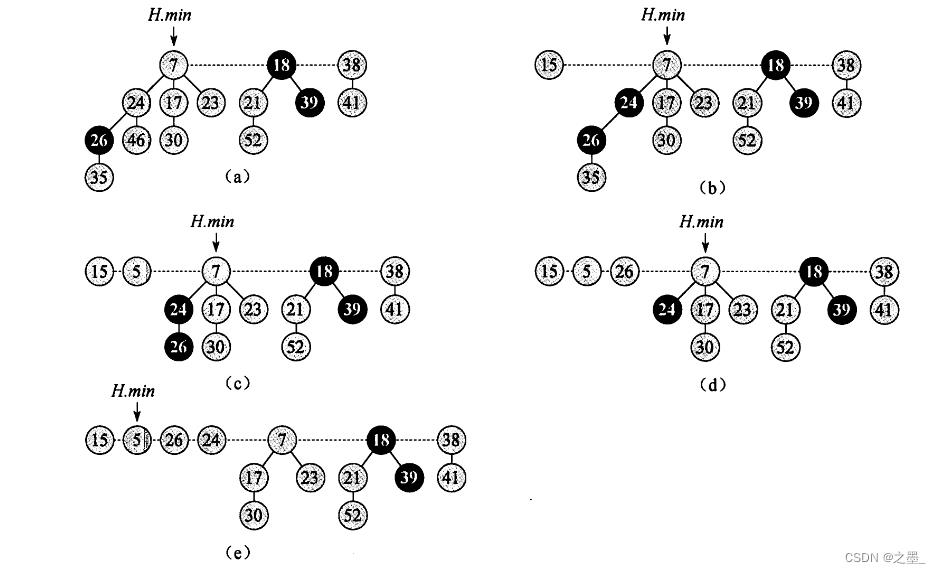
删除键值为3的根结点后将它的孩子结点链入根链
有一个0~3的数组表示当前堆中从0到最大度数,这个数组用于记录当前存在的度数,从而寻找相同度数的树
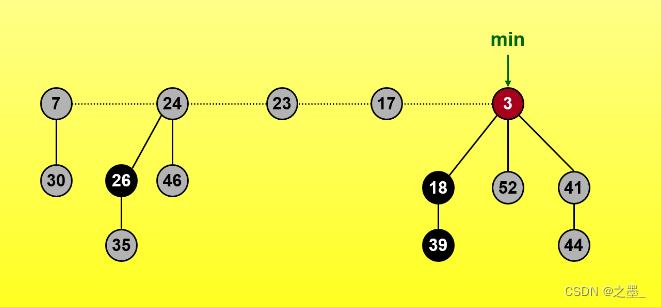
删除3后指针H.min指向根链中除3以外的某个根结点,没必要一定是新的最小结点,这里指针向右移动(双向链表,也可以指向17)
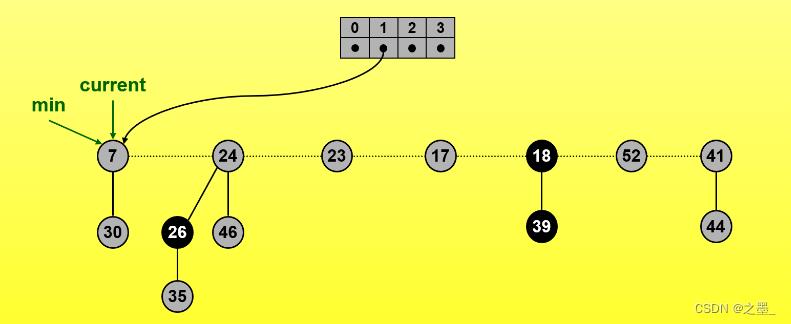
这里新的最小结点指向7,同时度数数组记录度数1
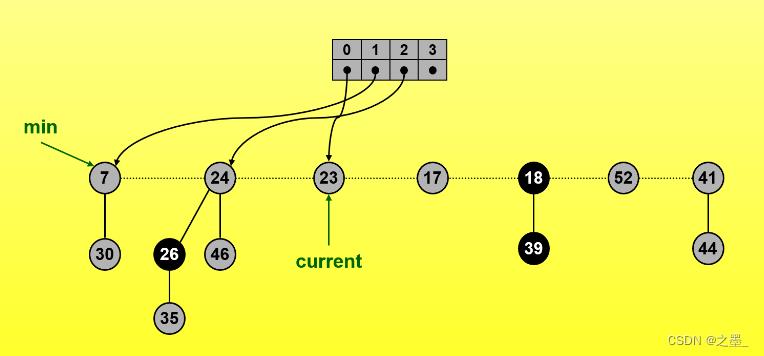
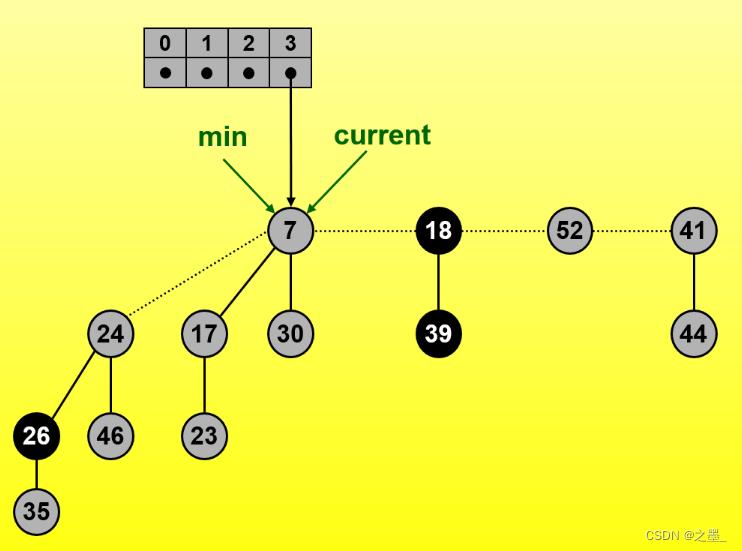
指针向右移,记录一个度数为2
继续右移找到一个度为0
右移找到相同度数0,合并两个度数为0的树,这里将较大值合并为较小值的子树(最小堆性质)
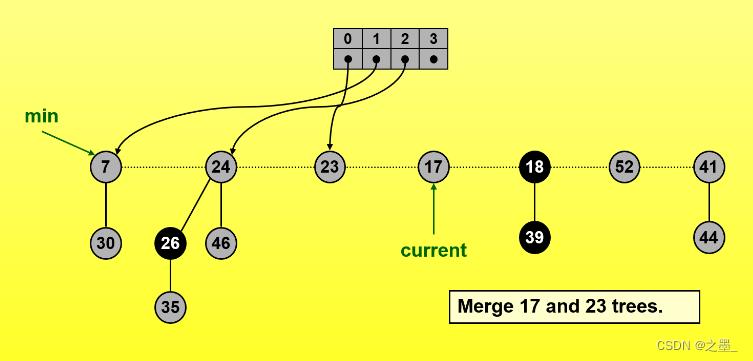
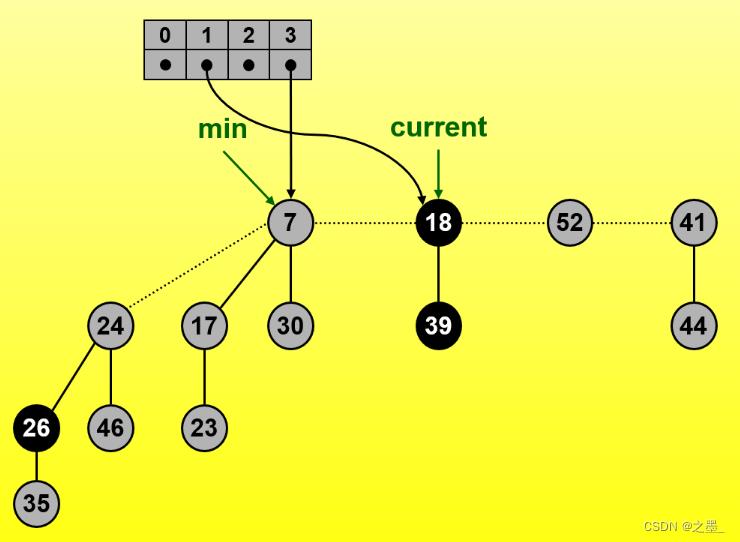
合并后得到一个度数为1的树,再次合并
合并后得到一个度为2的树,再次合并
得到一个度为3的树
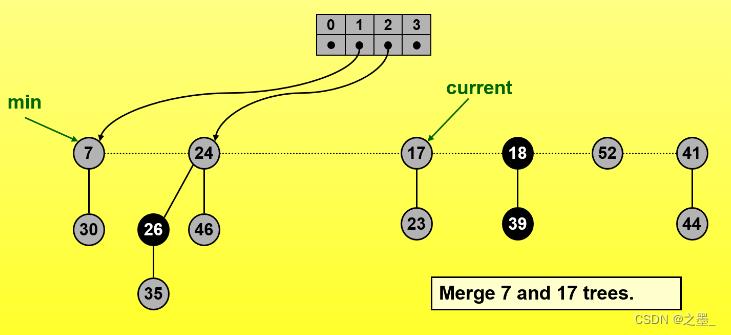
指针继续右移,记录度1
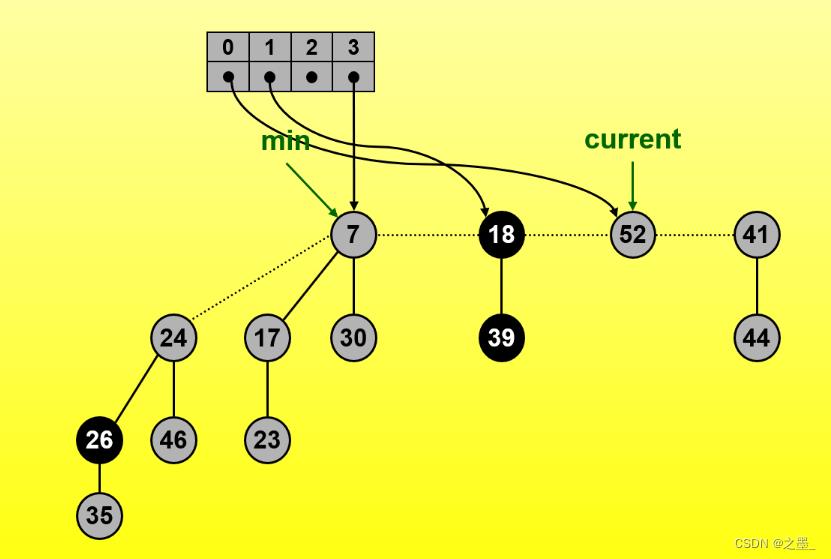
继续右移,记录度0
继续右移,找到一个度为2的树
合并相同度为1的树
继续右移
没有相同度数时执行完毕,最终得到一个斐波那契堆如下:
分析

- 实际开销:
O
(
D
(
n
)
+
t
(
H
)
)
O(D(n)+t(H))
O(D(n)+t(H))
- O ( D ( n ) ) : O(D(n)): O(D(n)):将最小结点的孩子结点加入根链中并更新最小结点
- O ( D ( n ) + t ( H ) ) : O(D(n)+t(H)): O(D(n)+t(H)):合并相同度的树
- 摊还时间复杂度:
O
(
D
(
n
)
)
O(D(n))
O(D(n))
- t ( H ′ ) ≤ D ( n ) + 1 t(H ') \\le D(n) + 1 t(H′)≤D(n)+1因为所有树度数均不同
- ∆ Φ ( H ) ≤ D ( n ) + 1 − t ( H ) ∆\\Phi(H ) \\le D(n) + 1- t(H) ∆Φ(H)≤D(n)+1−t(H)

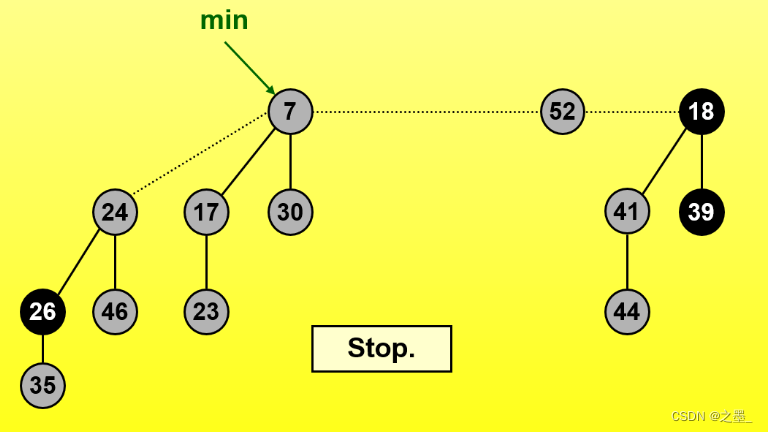
Decrease Key
第一种情况

- 最小堆性质未被破坏
- 有必要的话可以改变最小指针
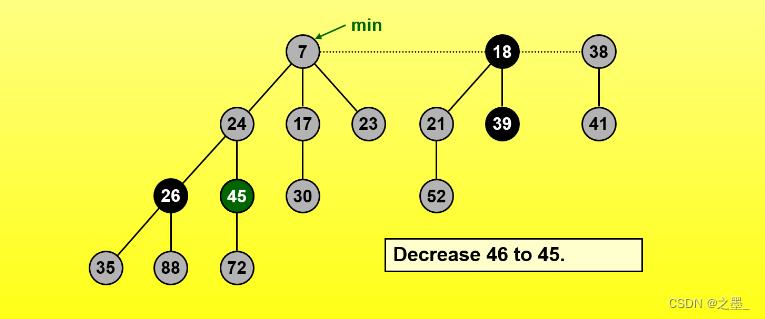
示例
剩余情况用书上的例子解释
附上伪代码



删除

最大度数的界


以上是关于高级数据结构—斐波那契堆与二项堆详细介绍(算法导论中科大USTC)的主要内容,如果未能解决你的问题,请参考以下文章