面试中的算法

Posted 2022-11-25 喵喵喵爱吃鱼

面试中的算法

面试，是大家从学校走向社会的第一步。大型互联网公司的校园招聘，从形式上说，一般分为2-3轮技术面试+HR面试。技术面试=基础知识和业务逻辑面试+算法面试。本章重点讲解面试的算法，助你拿到自己期望的offer。

本教程中的练习题，请移步 1024乐学编程-面试中的算法 进行练习。

您也可以在该网站免费学习到更多课程

判断链表是否有环

面试遇到的算法题目千变万化，不但要依靠扎实的算法基础，还需要随机应变。
下面我来考考你：有一个单向链表，链表中有可能出现“环”，就像下图这样。那么，如何用程序来判断该链表是否为有环链表呢?

我们可以从头结点开始遍历整个单链表

我们试一试。首先从头节点开始，依次遍历单链表中的每一个节点。每遍历一个新节点，就从头检查新节点之前的所有节点，用新节点和此节点之前所有节点依次做比较。如果发现新节点和之前的某个节点相同，则说明该节点被遍历过两次，链表有环；如果之前的所有节点中不存在与新节点相同的节点，就继续遍历下一个新节点，继续重复刚才的操作。

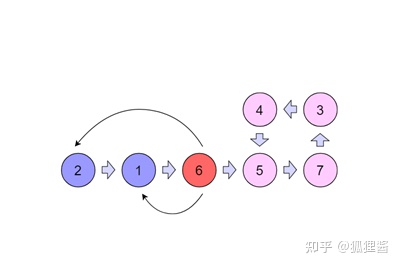
就像图中这样，当遍历链表节点6时，从头访问节点2和节点1，发现已遍历的节点中并不存在节点6，则继续往下遍历。
当第2次遍历到节点5时，从头访问曾经遍历过的节点，发现已经遍历过节点5，说明链表有环。
假设链表的节点数量为n，则该解法的时间复杂度为O(n²)。由于并没有创建额外的存储空间，所以空间复杂度为O(1)。
有没有效率更高的解法呢？

或者我们创建一个哈希表作为额外的储存。

首先创建一个以节点ID为Key的HashSet集合， 用来存储曾经遍历过的节点。然后同样从头节点开始，依次遍历单链表中的每一个节点。每遍历一个新节点，都用新节点和HashSet集合中存储的节点进行比较， 如果发现HashSet中存在与之相同的节点ID， 则说明链表有环， 如果HashSet中不存在与新节点相同的节点ID， 就把这个新节点ID存入HashSet中， 之后进入下一节点， 继续重复刚才的操作。请看下面的幻灯片

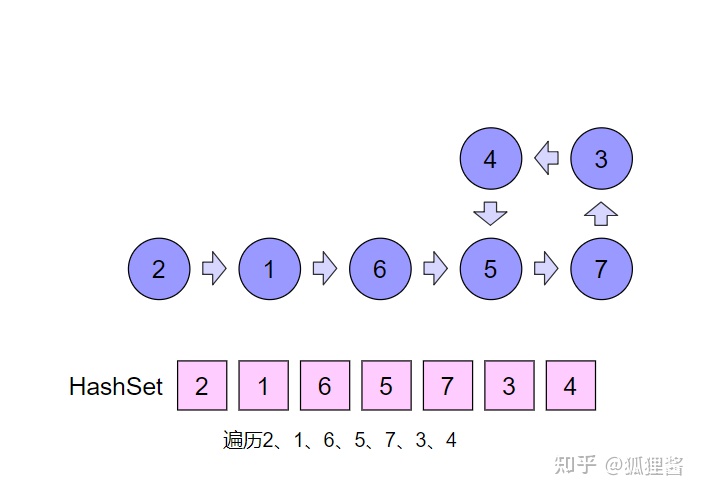
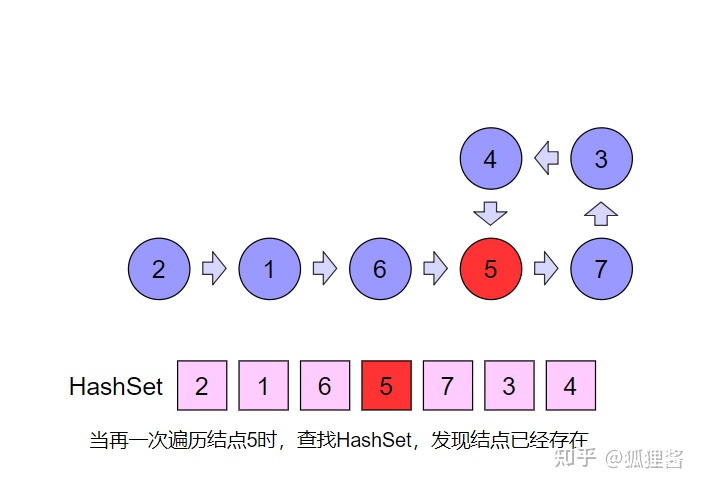
由此可知，链表有环。
这个方法在流程上和刚才的方法类似， 本质的区别是使用了HashSet作为额外的缓存。
链表的节点数量为n，则该解法的时间复杂度是O(n)。由于使用了额外的存储空间，所以算法的空间复杂度同样是O(n)。
这种方法在时间上已经是最优了，有没有可能在空间上也得到优化？

解题思路

有环链表的判断问题是很基础的算法题，许多面试官都喜欢考查，对于这道题，有一个很巧妙的方法，这个方法利用了两个指针。
首先创建两个指针 p1 和 p2 ， 让它们同时指向这个链表的头节点。然后开始一个大循环，在循环体中，让指针 p1 每次向后移动 1 个节点，让指针 p2 每次向后移动 2 个节点，然后比较两个指针指向的节点是否相同。如果相同，则可以判断出链表有环，如果不同，则继续下一次循环。请看下面的图片。

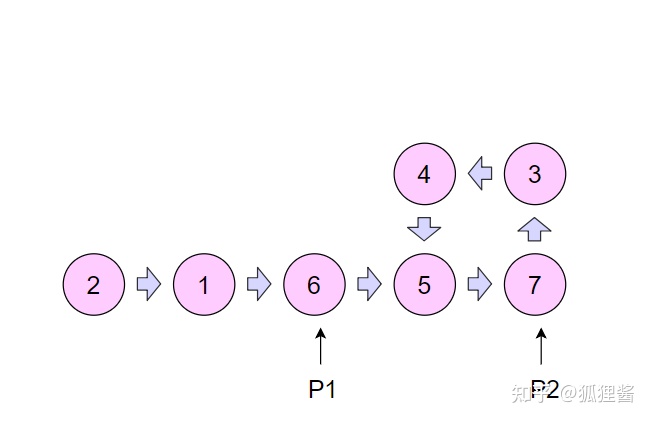
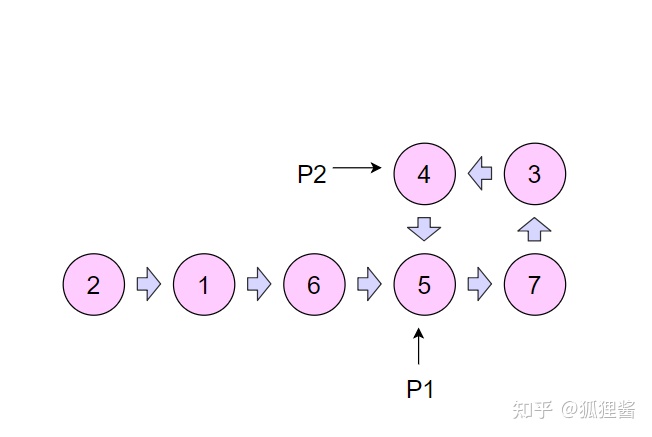
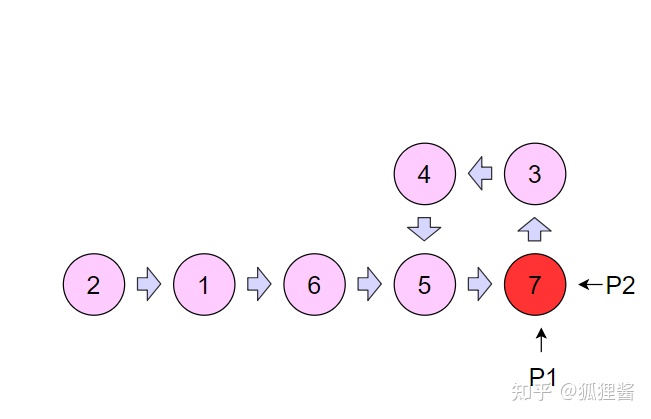
如上面的幻灯片，最后p1和p2指向的结点相通，说明链表有环。
此方法就类似于一个追及问题。在一个环形跑道上，两个运动员从同一地点起跑，一个运动员速度快，另一个运动员速度慢。当两人跑了一段时间后，速度快的运动员必然会再次追上并超过速度慢的运动员，原因很简单，因为跑道是环形的。
假设链表的节点数量为n，则该算法的时间复杂度为O(n)。除两个指针外，没有使用任何额外的存储空间，所以空间复杂度是O(1)。

代码实现如下：

#include <iostream>
using namespace std;
struct ListNode
 double value;
 ListNode *next;
;
bool isCircle(ListNode *head)
 ListNode *first = head, *second = head;
 while (first -> next != nullptr && second -> next -> next != nullptr)
 
        first = first -> next;
        second = second -> next -> next;
  if (first == second)
  
   return true;
   
 
   return false;

int main()
 ListNode *node1 = new ListNode;
    node1 -> value = 2;
 ListNode *node2 = new ListNode;
    node2 -> value = 1;
    node1 -> next = node2;
 ListNode *node3 = new ListNode;
    node3 -> value = 6;
    node2 -> next = node3;
 ListNode *node4 = new ListNode;
    node4 -> value = 5;
    node3 -> next = node4;
 ListNode *node5 = new ListNode;
    node5 -> value = 7;
    node4 -> next = node5;
    node5 -> next = node2;
    cout << "isCircle: " << isCircle(node1) << endl;
 return 0;

输出结果为：

isCircle: 1

1 也同样代表true 。

习题

下面我们做个练习题吧，还是接着上面，如果链表有环，如何求出环的长度呢？

给你个提示，当两个指针首次相遇，证明链表有环的时候，让两个指针从相遇点继续循环前进，并统计前进的循环次数，直到两个指针第2次相遇。此时，统计出来的前进次数就是环长。因为指针 p1 每次走1步，指针 p2 每次走2步，两者的速度差是1步。当两个指针再次相遇时，p2 比 p1 多走了整整1圈。

请移步到该网站的 《如何判断链表有环》课程中，习题在内容最后。

http://www.eluzhu.com:1818/my/course/60

最小栈的实现

再考你一个问题。
实现一个栈， 该栈带有出栈(pop) 、入栈(push) 、取最小元素(getMin) 3个方法。要保证这3个方法的时间复杂度都是O(1)。

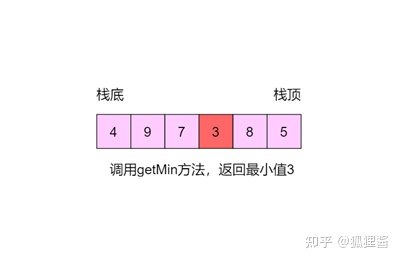
先创建一个整型变量min，用来储存栈中的最小元素。当第一个元素进栈时，把进栈的元素赋值给min，就是把栈中唯一的元素当做最小值。之后，每当一个新元素进栈，就和min比较大小。如果新元素小于min，则赋值给min，如果大于或等于min，则不做改变。当调用getMin方法时，直接返回min的值即可。

你想的太简单啦，你只考虑了进栈的场景，没考虑出栈的场景。

解题思路

原本，栈中最小元素是3，min量记录的值也是3，这时栈顶元素出栈了。

此时的min变量应该等于几呢？虽然此时的最小元素是4，但是程序并不知道。

所以说、只暂存一个最小值是不够的，我们需要存储栈中曾经的最小值，作为“备胎”。请看下面的幻灯片。

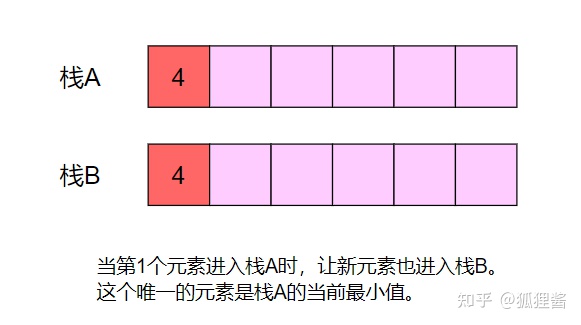
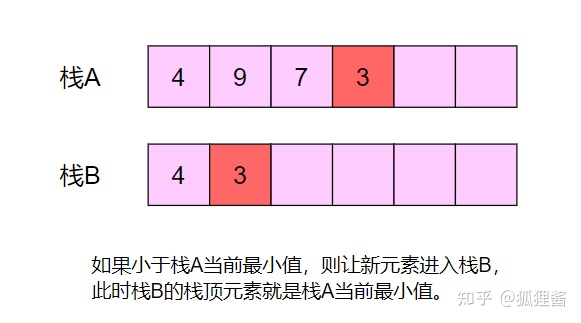
代码实现

当调用getMin方法时， 返回栈B的栈顶所存储的值， 这也是栈A的最小值。显然，这个解法中进栈、出栈、取最小值的时间复杂度都是O(1)，最坏情况空间复杂度是O(n)。
下面让我们看看代码如何实现。

#include <iostream>
#include <stdio.h>
#include <stack>
using namespace std;
class MinStack

public:
 MinStack()
 
 void push(int x)
      _data.push(x);
 if (_min.empty())
     _min.push(x);
 
 else
 if (x > _min.top())
     x = _min.top();
 
     _min.push(x);
 
 
 void pop()
     _data.pop();
     _min.pop();
 
 int top()
 return _data.top();
 
 int getMin()
 return _min.top();
 
private:
    std::stack<int> _data;
    std::stack<int> _min;
;
int main()
 MinStack it;
    it.push(4);
    it.push(9);
    it.push(7);
    it.push(3);
    it.push(8);
    it.push(5);
    cout << it.getMin() << endl;
    it.pop();
    it.pop();
    it.pop();
    cout << it.getMin() << endl;
 return 0;

这段代码第一个输出3 ，因为当时的最小值是3，第二个输出4，因为元素3出栈后最小值是4.

最后我们做一道练习题，请移步到该网站的 《最小栈的实现》课程中，习题在内容最后。

1024乐学编程-面试中的算法

好，我们这次先讲到这里，请进入作者主页继续学习后续的算法课程。或进入上面的地址免费学习完整的算法课程。