即将开源STD:用于3D位置识别的稳定三角形描述子
Posted Being_young
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了即将开源STD:用于3D位置识别的稳定三角形描述子相关的知识,希望对你有一定的参考价值。
文章:STD: Stable Triangle Descriptor for 3D place recognition
作者:Chongjian Yuan, Jiarong Lin , Zuhao Zou , Xiaoping Hong, and Fu Zhang
编辑:点云PCL
代码:https://github.com/hku-mars/STD.git(接受后开源)
欢迎各位加入免费知识星球,获取PDF论文,欢迎转发朋友圈。文章仅做学术分享,如有侵权联系删文。未经博主同意请勿擅自转载。
公众号致力于分享点云处理,SLAM,三维视觉,高精地图相关的文章与技术,欢迎各位加入我们,一起交流一起进步,有兴趣的可联系微信:920177957。本文来自点云PCL博主的分享,未经作者允许请勿转载,欢迎各位同学积极分享和交流。
摘要
在这项工作中,我们提出了一种新的全局描述子,称为稳定三角形描述子(STD),用于3D位置识别。对于三角形,其形状由边的长度或唯一夹角确定。此外,三角形的形状对于刚性变换是完全不变的。基于这一特性,我们首先设计了一种从3D点云中有效提取局部关键点并将这些关键点编码为三角形描述子的算法。然后,通过匹配点云之间描述子的边长(和一些其他信息)来实现位置识别。从描述子匹配对获得的点对应关系可以进一步用于几何验证,这大大提高了位置识别的准确性。在公共数据集(即KITTI、NCLT和Complex Urban)和我们的自收集数据集(使用非重复扫描固态激光雷达)上,将我们提出的系统与其他最先进的系统(即M2DP、 Scan Context扫描上下文)进行了广泛比较。所有的定量结果表明,STD具有更强的适应性,并且在精度上大大提高。为了分享我们的发现并为社区做出贡献,在GitHub上开源代码:https://github.com/hku-mars/STD.git。

图1.(a)显示了从查询点云提取的稳定三角形描述子(STD),(b) 显示从历史点云提取的STD。在(c)中,点云的这两个帧之间的STD匹配示例。正确匹配的STD描述子由白框表示,点云由STD提供的位姿进行匹配,这两帧点云由一个小视场激光雷达(Livox Avia)收集,并以相反的方向移动,导致低点云重叠和剧烈的视点变化。
主要贡献
本文开发了一种新的描述子,称为稳定三角形描述符(STD),它将场景中的任意三个关键点用三角形编码。与其他描述子中使用的多边形相比,三角形更稳定,因为三角形的形状是根据边的长度(或夹角)唯一定义的。与关键点周围的局部描述符相比,三角形的形状是具有旋转和平移不变的。为了提取三角形描述子的关键点,我们在平面上进行点云投影,并提取边界上的关键点。根据三角形的相似性进行匹配。图1显示了一个典型的STD位置识别案例,它成功地识别了在同一地点以相反视角收集的两个点云。具体而言,我们的贡献如下:
设计了一个三角形描述子,一个六维向量,由三条三角形边的长度和连接到每个三角形顶点的相邻平面的法向量之间的角度组成,描述子对旋转和平移完全不变,同时保持高度的可区分性。
提出了一种基于关键帧的快速关键点提取方法,为了表示场景的结构信息,将点云投影到平面边界并提取其中的关键点,这将与相邻关键点形成三角形描述子。
在多种场景(城市、室内和非结构化环境)和不同的激光雷达数据(传统旋转激光雷达和固态激光雷达)下评估我们的算法,充分的实验结果验证了该方法的有效性。
为了分享我们的发现并为社区做出贡献,让我们的读者能够在后续研究中快速复制我们的工作,我们在GitHub公开了代码。
主要内容
在本节将介绍如何构建描述子字典以及如何选择循环候选,最后,针对完整的回环检测流程,提出了基于RANSAC的环路检测和几何验证,我们的方法的总体流程如图2所示。
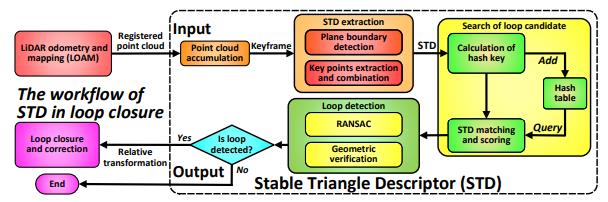
图2.STD描述子回环检测的工作流程,我们的方法从关键帧计算三角形描述子,然后使用哈希表作为描述子的数据库,以便快速存储和匹配,具有前10个描述符匹配分数的帧将被选为候选,一旦通过几何验证,循环候选将被视为有效循环,当循环被触发时,还将获得循环帧和候选帧之间的相对的位姿变换。
A、 稳定三角形描述子
受[ Segmatch: Segment based place recognition in 3d point clouds ]的启发,为了提高点云分割的稳定性,我们对关键帧执行循环检测,这些关键帧具有从几次连续扫描中累积的点云数据,因此无论特定的激光雷达扫描模式如何,都会增加点云密度。具体来说,我们使用LiDAR里程计[ Efficient and probabilistic adaptive voxel mapping for accurate online lidar odometry ]将每个新的输入点云配准到当前关键帧中。当子帧的数量累积到一定数量时,将创建新的关键帧。当给定点云的关键帧时,我们首先通过区域增长进行平面检测。具体来说,我们将整个点云划分为给定大小(例如,1米)的体素。每个体素包含一组点pi(i=1,…,N);然后我们计算点协方差矩阵∑:
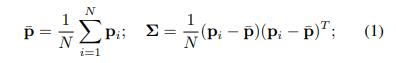
λk表示矩阵∑的第k个最大特征值。判断平面基本原则为:
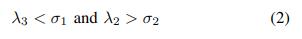
其中σ1和σ2是预设的超参数,根据这个标准,我们可以检查体素中的点是否形成平面,如果是,体素称为平面体素。然后,我们用任意的平面体素初始化平面,并通过搜索其相邻体素来扩展平面。如果相邻体素是相同的平面(具有相同的平面法线方向,距离低于阈值),则会将它们添加到正在增长的平面中。否则,如果相邻体素不在同一平面上,则会将其添加到正在增长的平面的边界体素列表中。上述增长过程重复,直到所有添加的相邻体素都展开,或达到边界体素(见图4)。

图4 平面区域生成的过程
对于边界体素,我们将其包含的点投影到相应的平面(见图5(a)和图5(b))。对于每个平面,我们创建一个图像,其中图像平面与平面重合,每个像素表示平面边界体素中包含的点的最大距离。然后选择一个点,它的5个像素中像素值最大∗5邻域作为关键点(见图5(c))。每个提取的关键点对应于输入点云中的3D点,并且可以与提取的平面的法线相关联。

图5.(a)边界体素中的点用黄色表示。(b) 这些点将投影到相邻平面上(蓝色点)。(c) 平面图像,其中每个像素表示边界体素中的点到平面的最大距离(以厘米为单位)。如果一个点在其5*5邻域中具有最大像素值,它将被视为关键点(红色点)。
利用关键帧中提取的关键点,我们构建一个k-D树,并为每个点搜索20个相邻点以形成三角形描述子。具有相同边长的冗余描述子将被剔除,每个三角形描述符子包含三个顶点,p1、p2和p3,以及投影法向量n1、n2和n3。此外,三角形的顶点按照边长规则按升序排列(见图3)。我们总结出一个三角形描述符∆ 具有以下内容:
p1、p2、p3:三个顶点,
n1、n3、n3:三个投影法向量,
l12、l23、l13:三面,和l12≤ I23≤ l13中。
q:三角形的中心,
k:描述子对应的帧编号,除了描述子之外,我们还将保存从该关键帧中提取的所有n个平面∏=(π1,π2,…,πn),用于以下几何验证步骤。
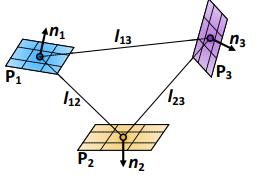
图3.标准三角形描述子,每个顶点p1、p2、p3对应于相邻平面。n1、n2、n3是相邻平面的法线向量。顶点按l12≤ I23≤ l13排列。
B、 循环候选帧搜索
由于可以从关键帧中提取数百个描述子,为了快速查询和匹配描述符,我们使用哈希表来存储所有描述子,使用描述子中具有旋转和平移不变性的六个属性来计算哈希键值,它们分别是边长l12、l23、l13和法线投影向量n1•n2、n2•n3、n1•n 3的点积,具有所有六个相似属性的描述符将具有相同的哈希键,因此将存储在同一容器中,对于查询关键帧,提取其所有描述子。对于每个描述符∆i,我们计算它的哈希键值,将其定位到哈希表中的相应容器中,并为该容器中有描述符的关键帧投票一次,当所有描述子处理查询关键帧中的i。具有前10个投票的关键帧将被选择为候选,其匹配的描述子被保存以供循环检测步骤使用。
Remark 1 :由于边界点被投影到从3D点云而不是从距离图像中提取的平面,因此提取的关键点对视角变化是不变的,此外,六个描述符属性对任何刚性变换都是不变的,因此,整体方法是具有旋转和平移不变性。
Remark 2:由于三角形边长的有序性和三角形的稳定性,当且仅当两个三角形的有序边的长度相等时,两个三角形就可以确保相同,而无需列举边对应关系。
C、 环路检测
当给定循环候选关键帧时,我们执行几何验证以消除由于不正确的描述子匹配对而导致的错误检测,由于三角形的形状是在确定边长后唯一确定的∆a与匹配∆b、 它们的顶点(pa1、pa2、pa3)和(pb1、pb2、pb3)自然匹配,然后,通过此点对应关系,我们可以通过奇异值分解(SVD)轻松计算这两个关键帧之间的相对变换T=(R,T):
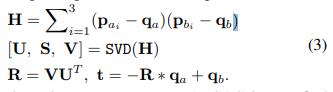
为了提高鲁棒性,我们使用RANSAC来找到最大化正确匹配描述子数量的变换帧。
基于该变换,我们计算当前帧和候选帧之间的平面重叠,以进行几何验证。设中心点g和法向量u表示体素中的平面π。表示当前帧的平面组为B,候选帧的平面群为C,刚体变换为C_BT,其中n是当前帧中的平面数并且m是候选帧中的面数,我们用的中心点构造一个k-D树(k=3),然后对于每个平面中心点Bgi,我们首先通过变换C_BT变换Bgi,然后在k-D树中搜索最近的点C_gj,并通过法向量差和点顶面距离判断两个平面是否重合:
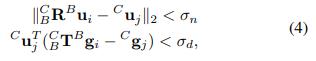
其中σn和σd是预设的超参数,用于确定平面是否重叠。如果一对平面满足等式(4)中的法向量和点到距离约束,则这对平面重合,检查当前帧的所有平面后,我们计算平面重合百分比(Nc):
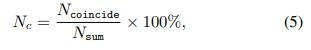
其中Nconmission是圆锥平面的数目,Nsum是当前帧的所有平面的数目。如果当前帧和候选帧的Nc超过某个阈值σpc,最终认为它是有效的回环检测。值得注意的是,基于平面的几何验证比基于ICP的方法更有效,因为平面的数量远小于点云的数量,此外,可以进一步优化方程(4)中的法向量差和点到平面距离,以获得更精确的环路校正位姿变换,这可以使用Ceres Solver轻松实现。我们将此优化过程定义为STD-ICP,并将在实验中验证STD-ICP的性能。
实验
为了验证我们的方法的有效性、鲁棒性和适应性,我们使用不同类型的激光雷达(机械旋转激光雷达和固态激光雷达)在不同场景(城市、室内和非结构化环境)中评估我们的算法,在每个实验中,将我们的方法与最先进的方法进行比较,所有实验都在同一系统上进行,该系统采用Intel i7-11700k@3.6 GHz,16 GB内存。
A、 基准数据集评估
在本实验中,我们对开放式城市数据集(包括KITTI里程数据集、NCLT数据集和复杂城市数据集)评估了我们的方法。所有数据都是在城市环境中使用具有不同扫描线的机械旋转激光雷达收集的。我们将我们的方法与其他两个全局描述符进行比较:Scan Context 和M2DP。我们每10帧将这些数据集累加为一个关键帧。如果查询关键帧和匹配关键帧之间的地面真实姿态距离小于20m,则认为检测为真阳性。
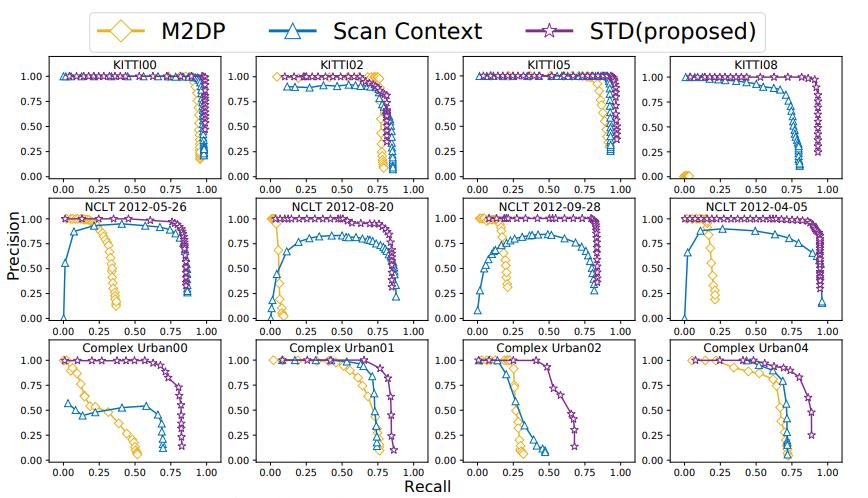
图6:KITTI、NCLT和复杂城市数据集的精度召回曲线
1) 精确召回评估:我们通过精确召回曲线来评估STD在不同平面重合阈值σpc时的性能,如图6所示。由于 Scan Context-50 在大多数情况下优于 Scan Context-10 ,因此我们仅显示 Scan Context-50 的结果,从结果来看,STD在几乎所有数据集中都优于 Scan Context和M2DP。然而,我们的方法并不局限于场景的高度,在这种场景中成功的环路检测如图7(a)所示,只有当场景的结构或平面特别稀疏时,我们的方法才会表现得很差,因为在这样的场景中提取的关键点很少,典型错误示例如图7(b)所示,这两个案例都来自NCLT数据集。

图7.狭窄场景中的挑战案例和STD的失败案例
2) 运行时间评估:我们在KITTI00上记录所有方法的计算时间,如图8所示。
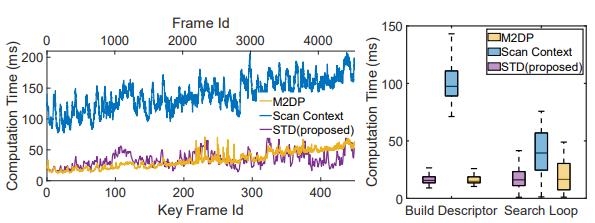
图8.KITTI00的时间评估
对于M2DP,我们使用默认参数的开源MATLAB代码进行测试。对于Scan Context修改了他们的MATLAB代码,有方法都使用0.5m体素网格的点云下采样。如图8所示,Scan Context和M2DP中每帧的时间消耗随着库中的帧数线性增加,而我们的方法没有这种线性增长趋势。这主要是因为我们使用哈希表作为数据库来存储描述符,这避免了为M2DP和Scan Context这样的历史描述符构建k-D树。总体而言,STD的计算时间与M2DP相似,但它处理的点数是M2DP的10倍。Scan Context使用增强的描述符,这增加了描述子构建和搜索回环的时间消耗。
3) 平面重合阈值选择:如图6所示,STD的精度召回曲线总是从等于1的精度下降,主要是由于选择了平面重合阈值σpc。当给定相对较大的σpc时,将只选择具有较大点云重叠的环路,这在我们使用的城市数据集中是100%准确的。当阈值降低时,将选择更多重叠较小的循环,从而引入可能的误报。我们在图9中记录了Kitti08上不同σpc对应的真阳性率和假阳性率,从图中可以看出,0.5∼ 0.6是一个良好的折衷值。
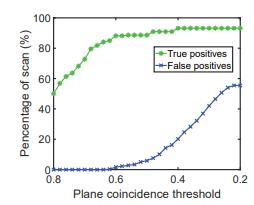
图9.平面重合阈值σpc对KITTI08的真阳性率和假阳性率的影响
4) 定位评估:一些其他描述子可以在执行回环检测时估计环路帧和候选帧之间的偏航角,我们提出的描述子进一步改进了该函数,因为我们可以提供循环帧和候选帧之间所有六个自由度的相对变换,而无需额外计算。为了验证这一点,我们在KITTI00的回环节点上进行了实验,对于每个回环节点,我们将相对于匹配帧的变换设置为从邻域±5◦ 在每个旋转轴上和在每个平移轴上的±5m。
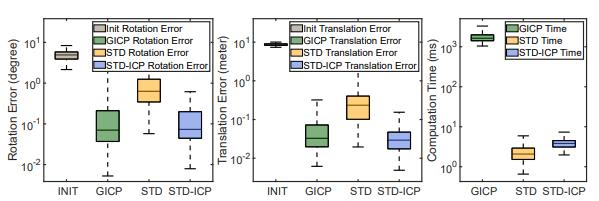
图10显示了GICP、STD和STD-ICP的误差和计算时间,STD-ICP可以实现与GICP相似的精度,旋转和平移的方差较小,这是因为STD为STD-ICP提供了一个良好的初始值,而GICP可能具有重叠较少的局部最优环内节点。此外,STD和STDICP比GICP花费的时间要少得多,仅不到GICP的1%。这是因为与点云的大小(超过100K)相比,平面的数量(数百)非常小。
B、 适用于其他类型的激光雷达
在本实验中,为了评估STD在不同环境和使用不同激光雷达时的适应性和适用性,我们使用Livox系列固态激光雷达在城市、非结构化和室内环境中进行了实验。在图11中显示了公园和室内环境的精细点云图和回环节点。

图11.公园和室内环境中的精细点云图,回环节点由白框表示
结果分析:STD和M2DP的精度召回曲线如图12所示。
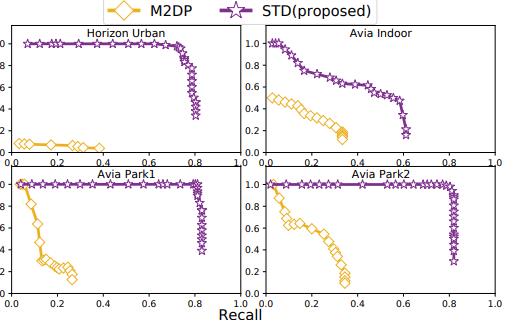
从图中可以看出,M2DP在Livox数据集上表现不佳,这主要是因为建筑物每层的走廊非常相似,导致相对较低的精确度和召回率,但是,我们仍然可以为回环校正提供一定数量的有效环路节点,以便LiDAR环路闭合可以应用于室内映射,例如多层停车场、博物馆等。
总结
本文提出了一种基于三角形的全局描述子STD,这是一个基于平面检测和边界投影的高效关键点提取算法,用于提取具有几何特征的关键点,这些关键点与其相邻点形成三角形描述符,这种组合大大提高了描述子的旋转和平移不变性。此外,三角形的稳定性和唯一性使得该描述子自然适合于位置识别中的相似性比较。为了加快描述符的查询和匹配,我们使用哈希表作为数据库来存储所有历史描述子,这避免了在循环搜索中构建k-D树,与其他全局描述子相比,STD不仅在公共数据集上表现更好,而且对不同环境和激光雷达类型的适应性更强。
更多详细内容请加入知识星球查看原文。
资源
自动驾驶及定位相关分享
【点云论文速读】基于激光雷达的里程计及3D点云地图中的定位方法
自动驾驶中基于激光雷达的车辆道路和人行道实时检测(代码开源)
更多文章可查看:点云学习历史文章大汇总
SLAM及AR相关分享
结构化PLP-SLAM:单目、RGB-D和双目相机使用点线面的高效稀疏建图与定位方案
如果你对本文感兴趣,请后台发送“知识星球”获取二维码,务必按照“姓名+学校/公司+研究方向”备注加入免费知识星球,免费下载pdf文档,和更多热爱分享的小伙伴一起交流吧!
以上内容如有错误请留言评论,欢迎指正交流。如有侵权,请联系删除
扫描二维码
关注我们
让我们一起分享一起学习吧!期待有想法,乐于分享的小伙伴加入免费星球注入爱分享的新鲜活力。分享的主题包含但不限于三维视觉,点云,高精地图,自动驾驶,以及机器人等相关的领域。
分享及合作方式:微信“920177957”(需要按要求备注) 联系邮箱:dianyunpcl@163.com,欢迎企业来联系公众号展开合作。
点一下“在看”你会更好看耶

以上是关于即将开源STD:用于3D位置识别的稳定三角形描述子的主要内容,如果未能解决你的问题,请参考以下文章