杠上数据结构 - 树

Posted 2022-11-22 星火燎原2016

线性与非线性

线性： 指的是元素之间是 “一对一” 的关系，比如只有唯一 一个"前驱"和唯一一个"后继"。

非线性： 指的是元素之间是一对多的关系，比如 “树” 中节点可能有多个孩子节点，“图” 中可能有多个元素与之关联。

树

树是一种非线性的数据结构，是由 n （n >= 0）个节点组成的有限集合。如果 n = 0，则树是空树。除了根节点外，其余节点被分成 M (M > 0) 个互不相交的集合 T1, T2, T3,……Tn, 其中每一个集合又是一棵结构和树类似的子数，每棵子树的根节点有且只有一个前驱，有 0 个或多个后继。

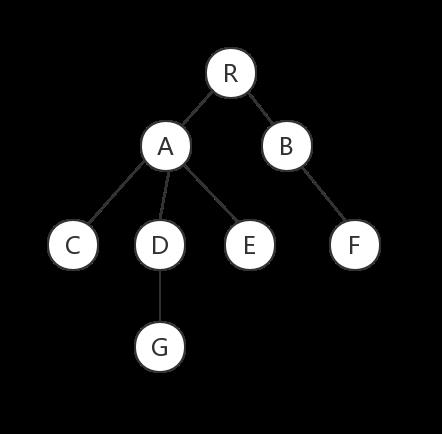
树有关的基本概念：

• 节点： 节点包含数据和指向其他节点的指针。
• 根节点： 树的第一个节点。
• 节点的度： 该节点所拥有的子树的个数。
• 树的度： 树中所有节点的度的最大值称为该树的度。
• 叶子节点： 没有子节点的节点，也称终端节点。
• 父子节点： 一个节点 father 指向另一个节点 child ，则 child 为孩子节点， father 为父节点。
• 兄弟节点： 具有相同父节点的节点互为兄弟节点。
• 祖先节点： 从根节点开到该节点所经过的所有节点都是该节点的祖先。
• 子孙节点： 以某节点为根的子树中任意一个节点都称为该节点的子孙节点。
• 树的高度： 树中距离根节点最远节点的路径长度。

树的存储结构

1. 双亲表示法
2. 孩子表示法
3. 孩子兄弟表示法

1. 双亲表示法

以一组地址连续的空间(数组)存储树的节点，同时在每个节点中，附设一个指示器指示其双亲节点在数组中的位置。

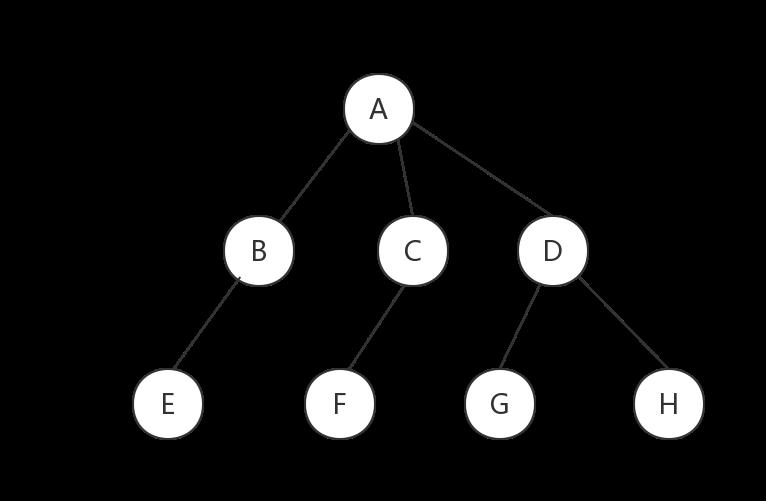
下标	data	parent
0	A	-1
1	B	0
2	C	0
3	D	0
4	E	1
5	F	2
6	G	3
7	H	3

二叉树

二叉树： 二叉树的每个节点至多只有二棵子树，子树有左右之分且顺序不能颠倒，左的称为 左子树，右边的称为右子树。

二叉树特点

• 每个节点至多有两棵子树，即二叉树中不存在度大于2 的节点。

• 二叉树的子树有左右之分，且子树的次序不能颠倒。

• 二叉树第 i 层上的节点数目最多为 $2^{i-1}(i>=1)$

• 深度为 k 的二叉树至多有 $2^k-1$ 个节点 (k >=1)

• 包含 n 个节点的二叉树的高度至少为 $log2(n+1)$

• 在任意一个二叉树中，若叶子节点的个数为 n , 度为 2 的节点的个数为 m , 则 n= m +1

二叉树的种类

(1) 斜树

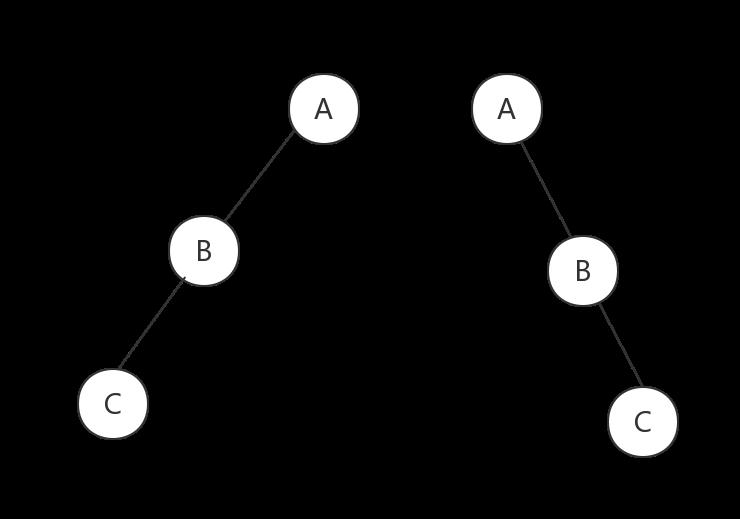
(2) 满二叉树

叶子节点都在同一层，并且除了叶子节点外的所有节点都有两个子节点。

(3) 完全二叉树

对于一颗二叉树，假设起深度为 d (d > 1) , 除了第 d 层外的所有节点构成满二叉树，且第 d 层所有节点从左向右连续的紧密排列，这样的二叉树称为完全二叉树。

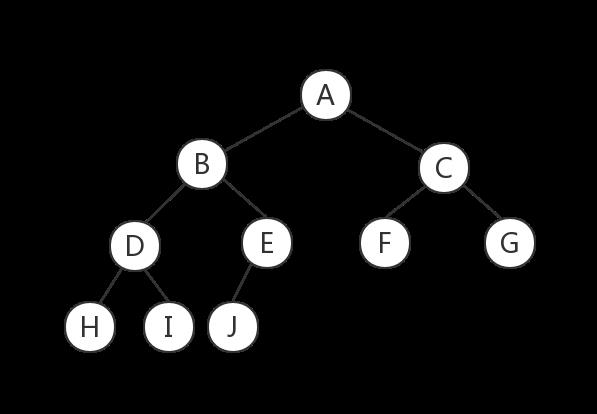
（4）平衡二叉树

它是一颗空树或 他的左右两个子树的高度差的绝对值不超过 1， 并且左右两个子树都是一颗平衡二叉树，同时，平衡二叉树必定是二叉搜索树。

（5）二叉查找树(二叉排序树)

若任意节点的左子树不为空，则左子树上所有节点的值均小于它的根节点的值；

若任意节点的右子树不为空，则右子树上所有节点的值均大于它的根节点的值；

任意节点的左，右子树也分别为 二叉查找树。

（6）红黑树

1. 节点是红色或黑色的
2. 根节点是黑色的
3. 每个叶子节点是黑色的
4. 每个红色节点的两个子节点都是黑色的，因此每个叶子节点到根节点的所有路径不能有两个连续的红色节点。
5. 从任意一个节点到其每个叶子节点的所有路径都包含相同数量的黑色节点。