零知识证明BLS12-381介绍译文
Posted Anyanyamy
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了零知识证明BLS12-381介绍译文相关的知识,希望对你有一定的参考价值。
原文链接:https://hackmd.io/@benjaminion/bls12-381#BLS12-381-For-The-Rest-Of-Us
强烈建议阅读原文。
Everything I wish I’d known before I started fiddling with this thing.
椭圆曲线BLS12-381最近很火。许多协议使用它来实现数字前面和零知识证明:Zcash, Ethereum 2.0等等。然而目前的介绍都很难懂。本文不介绍椭圆曲线和群的性质,读者需要自行了解。
Motivation 动机
BLS12-381是 pairing-friendly 的椭圆曲线。基于双线性对(pairing)的密码学已经发展了很多年,被用于简短数字签名(short digital signature)、基于身份的密码学(identity-based cryptography)、单轮多方密钥交换等领域。
pairing-friendly 的椭圆曲线是指有很好的嵌入度(favourable embedding degree)、很大的质数阶子群(large prime-order subgroup)。这种椭圆曲线很少,BLS曲线就是特地构造的符合条件的曲线。
About curve BLS12-381
History 历史
BLS12-381是Sean Bowe在2017年设计的椭圆曲线,用于对Zcash协议进行更新,该曲线pairing-friendly并且可用于高效构建zkSnarks。
Naming 命名
BLS12-381属于BLS曲线家族,由Barreto, Lynn, and Scott发明。
12:曲线的嵌入度(后面再介绍概念)
381:曲线上的点坐标表示所需的bit位数,即有限域的modulus q 的位数。因为点的坐标来自质数阶有限域,我们可以用384位(48Bytes)来表示每个域元素,留3 bit来做标志位或者算术优化。这个位数是由安全需求与实现高效所共同决定的。
Curve equation and parameters 曲线公式和参数
BLS12-381的最基本的椭圆曲线公式为: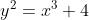
曲线的参数由一个参数x来决定,注意这里的x不是公式里的自变量,只是一个决定曲线的参数值。x需要满足以下条件:
1. x具有low hamming weight,很少有位被置为1。This is particularly important for the efficiency of the algorithm that calculates pairings (the Miller loop).
2. 有限域的modulus q是质数,位数<=383位。which makes 64-bit or 32-bit arithmetic on it more efficient.
3. 子群的阶 r 是质数,且位数<=255位。which makes 64-bit or 32-bit arithmetic on it more efficient.
4. 安全等级是128位。
5. 为支持zkSnark需要一些限制,这里不翻译了。
最终选定的x= -0xd201000000010000 ,从这个参数可以计算出BLS12-381的其他参数:

Field extensions 域扩展
域扩展对椭圆曲线双线性对很重要。12不仅是嵌入度,也是我们需要使用的域扩展的degree
有限域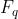 :一些模
:一些模 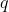 的整数,比如 0, 1, .. q-1。 那
的整数,比如 0, 1, .. q-1。 那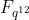 是什么样的呢?
是什么样的呢?
我目前没找到很直观的解释,以下是我的解释。
首先构建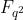 ,把域元素表示为1阶多项式,例如
,把域元素表示为1阶多项式,例如 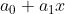 ,可以简写为
,可以简写为 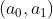
于是加法变成了如下操作:
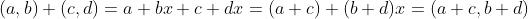
只需要把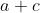 和
和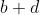 模
模 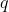 即可。
即可。
乘法变成了:
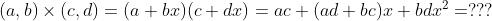
该怎么处理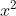 的系数呢?
的系数呢?
我们需要化简多项式,使得它小于2阶。在这个例子中,我们制定规则 ,当然也可以制定其他规则,只要满足以下两个条件即可
,当然也可以制定其他规则,只要满足以下两个条件即可 :
:
1. 需要是一个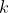 阶多项式,其中
阶多项式,其中 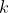 是extension degree。例子中
是extension degree。例子中 
2. 在我们扩展的域中是不可约的,不能被分解成更多低次多项式
应用我们制定的规则,乘法变成了:
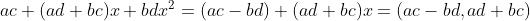
这跟复数算术很像: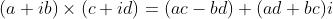
这不是巧合!因为复数就是实数的二次扩展 quadratic extension
复数不能再扩展,因为在复数上没有不可约多项式了。
但是对有限域,如果在 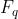 中能找到
中能找到 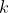 阶不可约多项式,通常就能把域扩展到
阶不可约多项式,通常就能把域扩展到 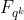 ,并且把扩展域中的元素表示成
,并且把扩展域中的元素表示成  阶多项式:
阶多项式: ,简写成:
,简写成: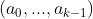
我们可以精心设计这种模约减(modular reduction)的规则,以实现twisting operation。
通常,大的扩展域例如 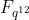 are implemented as towers of smaller extensions。
are implemented as towers of smaller extensions。
The curves 椭圆曲线具体参数
BLS12-381中其实有2条曲线,而不是一条,其实这两条的椭圆曲线公式只是定义在不同的域上。
本质上:BLS12-381使用了两条定义在有限域上的椭圆曲线
一、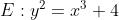
即上面介绍的最基本的一条椭圆曲线方程,又称为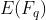 ,满足方程的
,满足方程的 都属于有限域
都属于有限域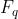
群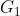 是定义在椭圆曲线上、阶为 r 的循环群,由有限域中的基础点base point BP=(x,y)生成
是定义在椭圆曲线上、阶为 r 的循环群,由有限域中的基础点base point BP=(x,y)生成
【1】BLS12-381的具体参数:
https://tools.ietf.org/id/draft-yonezawa-pairing-friendly-curves-02.html#rfc.section.1.1
参数含义:
p:有限域的参数,即椭圆曲线上的点坐标都要mod p,是381位的,这里写法不同,文中使用q
r:子群G1的阶,即点的总个数
BP:群的生成元
h: A subgroup’s cofactor is the ratio of the size of the whole group to the size of the subgroup.
即大群的阶/子群的阶
a, b:方程的系数


二、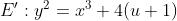
是twisted curve,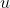 其实就是上面定义的复数
其实就是上面定义的复数 ,定义在二次扩展域
,定义在二次扩展域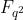 上,又称为
上,又称为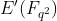
群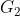 是定义在椭圆曲线上、阶为 r 的循环群,由有限域
是定义在椭圆曲线上、阶为 r 的循环群,由有限域 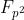 (只是写法不同,上面用的q字母)中的基础点base point BP'=(x',y')生成
(只是写法不同,上面用的q字母)中的基础点base point BP'=(x',y')生成
群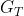 是阶为 r 的定义在有限域
是阶为 r 的定义在有限域 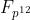 上的乘法群的子群。
上的乘法群的子群。
双线性映射为: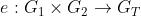
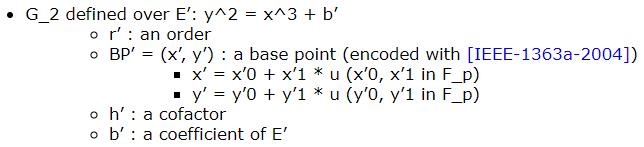

The Subgroups 子群
双线性对的定义不再赘述。
由于简单的椭圆曲线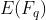 只有1个阶为r的大的子群,无法单独在这条椭圆曲线上定义pairing
只有1个阶为r的大的子群,无法单独在这条椭圆曲线上定义pairing
然而,如果保留定义的扩展域,可以证明存在椭圆曲线拥有不止1个子群。下面不太好翻译,直接放原文:
However, if we keep extending the field over which E is defined, it can be proved that we eventually find a curve that has more than one subgroup of order rr (in fact, r+1 of them). That is, for some k, E(Fqk)[6] contains other subgroups of order r that we can use. One of these subgroups contains only points having a trace of zero[7], and we choose that subgroup to be G2.
This number k, the amount that we need to extend the base field by to find the new group, is called the embedding degree of the curve, which in our case is the “12” in BLS12-381. We’ll discuss embedding degree more in a moment.
在椭圆曲线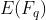 上有阶为r的群
上有阶为r的群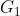 在椭圆曲线
在椭圆曲线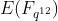 上有阶为r的群
上有阶为r的群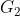
Twists
然而,在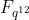 上算术运算低效,而椭圆曲线操作需要大量算术操作,因此上面这个群
上算术运算低效,而椭圆曲线操作需要大量算术操作,因此上面这个群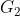 不好用。
不好用。
twist类似于坐标变换,可以用于把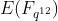 曲线转到定义在low degree filed的曲线,且仍具有阶为r的子群。
曲线转到定义在low degree filed的曲线,且仍具有阶为r的子群。
A twist is something like a coordinate transformation. Rather wonderfully, this can be used to transform our E(Fq12) curve into a curve defined over a lower degree field that still has an order r subgroup. Moreover, this subgroup has a simple mapping to and from our G2 group[9].
BLS12-381使用sextic twist,它把扩展域的度降低了6倍。因此,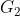 可以定义在
可以定义在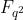 而不是定义在
而不是定义在 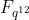 上,这样能大大降低复杂度。
上,这样能大大降低复杂度。
如果可以找到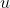 使得
使得 ,那么twisting transformation可以定义为:
,那么twisting transformation可以定义为:
这个转换把原来的曲线: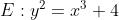 转换成曲线:
转换成曲线: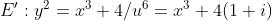
这两个看起来不同,但是实际上是同样的对象 the same object presented with respect to coefficients in different base fields[10]
因此最终使用的两个群为:
 其中:
其中: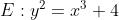
 其中:
其中: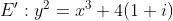
这也是 BLS12-381看起来用了2条曲线的原因。
注意: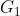 中的点的坐标是整数,而
中的点的坐标是整数,而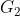 中点的坐标是一对对复数,因此
中点的坐标是一对对复数,因此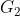 的点存储空间是
的点存储空间是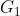 的两倍,成本更高。
的两倍,成本更高。
Pairings 双线性对
双线性对即上面提到的: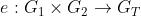
通常将两个点映射到一个点: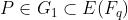
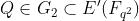
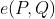 落到
落到 
具有以下性质:
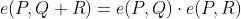
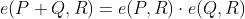
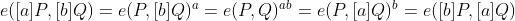
最后一条经常用于验证数字签名
Embedding degree 嵌入度
嵌入度 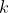 :最小的正整数满足
:最小的正整数满足  能整除
能整除 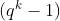
在BLS12-381中  是
是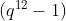 的最大素数因子
的最大素数因子


选择嵌入度是平衡安全与效率。在安全性方面,更高的嵌入度使得在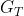 中的离散对数问题更难求解。然而更高的嵌入度也意味着更低效的计算。
中的离散对数问题更难求解。然而更高的嵌入度也意味着更低效的计算。
Security level 安全级别
密码系统的安全性是由bits来衡量的。一般来说,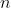 -bit安全是指大概需要
-bit安全是指大概需要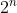 次操作来攻破密码。
次操作来攻破密码。
对于椭圆曲线密码学,安全性指的是离散对数问题。即给出点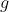 和
和 ,寻找
,寻找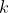 是非常困难的。
是非常困难的。
对于基于双线性对的曲线,在使用的3个群中离散对数问题都必须很难求解。

BLS12-381可以提供大约128bit的安全等级,实际上可能在117~120bits之间。
Cofactor
A subgroup’s cofactor is the ratio of the size of the whole group to the size of the subgroup.
cofactor: 大群的阶/子群的阶
一般椭圆曲线密码学要求cofactor很小,通常是1,为了防止离散对数上的small subgroup attack
在pairing-based密码学中,cofactor可能非常大
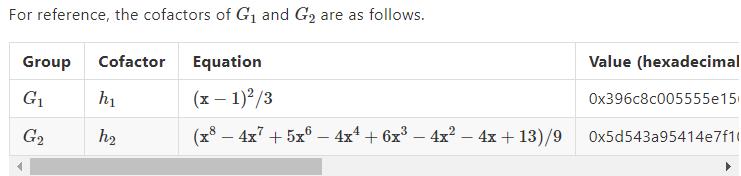
cofactor的用途:乘以cofactor就能把椭圆曲线上的任一点转换到对应的子群 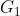 或者
或者 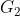
在做hash to curve操作时很重要,首先把在椭圆曲线上make a point,然后映射到子群上,也被称为 cofactor clearing.
Roots of unity
这一节不太懂,直接放原文:
Just a note on roots of unity, because they come up in two completely different and unrelated contexts, which can be confusing.

Using curve BLS12-381
BLS digital signatures
以上是关于零知识证明BLS12-381介绍译文的主要内容,如果未能解决你的问题,请参考以下文章