轻松解决TSP问题之强化学习(BaseLine)
Posted Huterox
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了轻松解决TSP问题之强化学习(BaseLine)相关的知识,希望对你有一定的参考价值。
文章目录
前言
由于这个时间关系(好吧其实是我懒),咱们的话就只写了这个最简单的一个BaseLine版本。那么后面还有Lite,Plus版本,区别的话就是神经网络模型的一个区别,其他的思想都是一样的。那么为什么不写后面的版本呢,一方面是懒,另一方面是,这样搞,我后面怎么水呀。而且一步到位的话,这个阅读量还是挺大的。那么后续的版本什么时候更新呢,这个不急,而且改进的点也很简单。
那么本文也是,TSP系列的第三篇文章,也是作为一个拓展文章,那么关于原理部分的话,这里就不细说了,需要一定的基础进行观看。
强化学习
那么咱们这边所使用到的强化学习算法呢还是这个DDPG,为什么用这个,待会在模型阐述的时候我会进行说明。那么咱们这边简单聊一下DDPG,之后的话结合到我们具体的TSP求解当中。
强化学习
强化学习是机器学习领域之一,受到行为心理学的启发,主要关注智能体如何在环境中采取不同的行动,以最大限度地提高累积奖励。
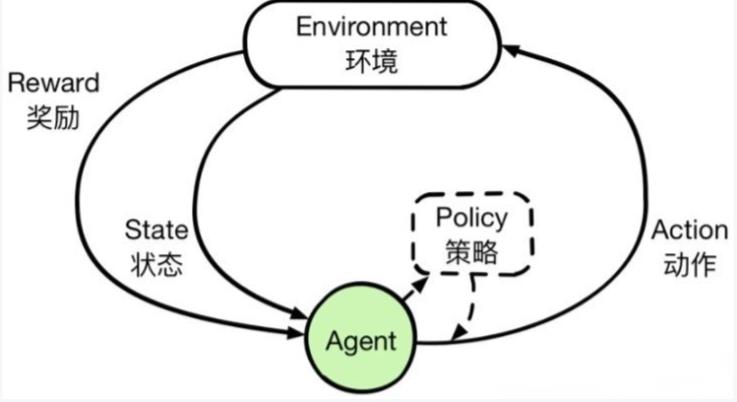
关键概念
关于强化学习这里面主要有几个概念。
智能体
强化学习的本体,作为学习者或者决策者。环境
强化学习智能体以外的一切,主要由状态集合组成。状态
一个表示环境的数据,状态集则是环境中所有可能的状态。动作
智能体可以做出的动作,动作集则是智能体可以做出的所有动作。奖励
智能体在执行一个动作后,获得的正/负反馈信号,奖励集则是智能体可以获得的所有反馈信息。策略
强化学习是从环境状态到动作的映射学习,称该映射关系为策略。通俗的理解,即智能体如何选择动作的思考过程称为策略。目标
智能体自动寻找在连续时间序列里的最优策略,而最优策略通常指最大化长期累积奖励。
因此,强化学习实际上是智能体在与环境进行交互的过程中,学会最佳决策序列。
基本框架
强化学习主要由智能体和环境组成。由于智能体与环境的交互方式与生物跟环境的交互方式类似,因此可以认为强化学习是一套通用的学习框架,是通用人工智能算法的未来。
强化学习的基本框架如图所示,智能体通过状态、动作、奖励与环境进行交互。
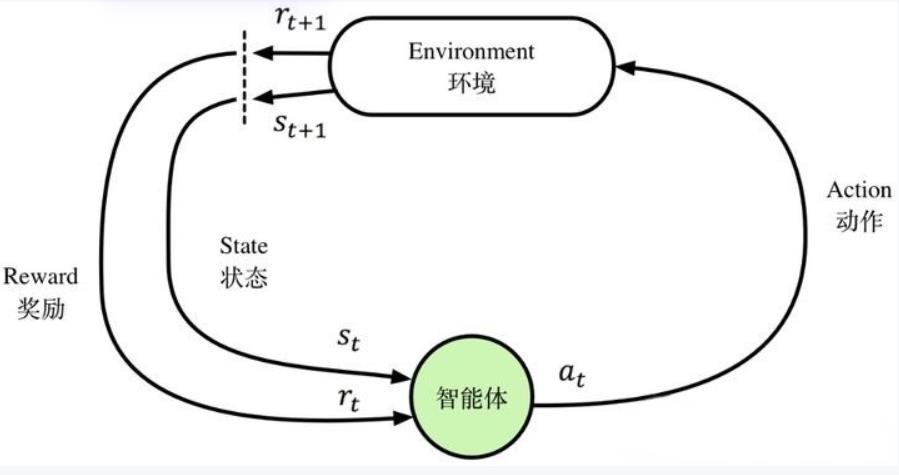
在线学习(简述)
这里先做一个简述,后面我们会进行深入一点的探讨。
关于强化学习呢,还可以划分:在线学习和离线学习。在论文当中使用的DDPG,使用的是在线学习策略,所以本文也是简单说一下在线学习和离线学习。
这里以QLearn 为代表

离线学习(简述)
离线学习其实和在线学习类似,区别在于选择动作的时候,离线学习单纯按照价值最大的去现在。而在线学习的话还是有一定概率来选择并不是当前价值最大的动作。

实际核心代码的区别:
Q Learn
def QLearning():
QTable = Init(N_STATES, ACTIONS)
for ecpho in range(ECPHOS):
step_counter = 0
S = 0
# 是否回合结束
isWin = False
updateEnvShow(S, ecpho, step_counter)
while not isWin:
#选择行为
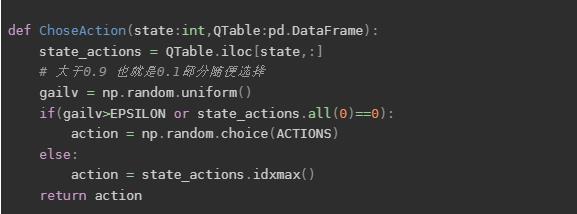
A = ChoseAction(S, QTable)
# 得到当前行为会得到的Reward,以及下一步的情况
S_, R = GetReward(S, A)
# 估算的(状态-行为)值
q_predict = QTable.loc[S, A]
if S_ != 'win':
# 实际的(状态-行为)值 这个就是类似与G1
q_target = R + GAMMER * QTable.iloc[S_, :].max()
else:
# 实际的(状态-行为)值 (回合结束)
q_target = R
isWin = True
QTable.loc[S, A] += ALPHA * (q_target - q_predict) # QTable 更新
S = S_ # 探索者移动到下一个 state
# 环境更新显示
updateEnvShow(S, ecpho, step_counter+1)
step_counter += 1
return QTable
Sarsa 离线学习
def SARSA():
QTable = Init(N_STATES, ACTIONS)
for ecpho in range(ECPHOS):
step_counter = 0
S = 0
# 是否回合结束
isWin = False
updateEnvShow(S, ecpho, step_counter)
A = ChoseAction(S, QTable) # 先初始化选择行为
while not isWin:
S_, R = GetReward(S, A)
try:
A_ = ChoseAction(S_, QTable)
except:
# 这里说明已经到了终点(如果报错)
pass
q_predict = QTable.loc[S, A]
if S_ != 'win':
q_target = R + GAMMER * QTable.iloc[S_, :].max()
else:
q_target = R
isWin = True
QTable.loc[S, A] += ALPHA * (q_target - q_predict) # QTable 更新
S = S_
A = A_
updateEnvShow(S, ecpho, step_counter+1)
step_counter += 1
return QTable
对于离线学习而言,如果从上面的代码来改的话,那么只需要把动作选择函数的概率调整为1,并且先提前选择一个价值最大的动作即可。
无论是对于在线学习还是离线学习,其目的都是需要得到这样一张表:
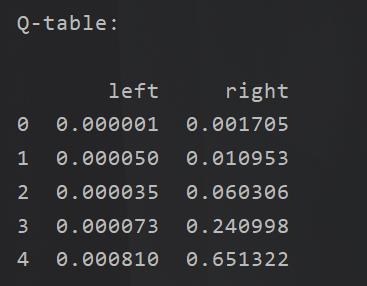
Qlearn
现在我们来好好的聊了里面的一些大体的细节。
马尔可夫决策
我们这里只讲大概几个和QLearn 关系比较紧密的东西。
里面比较详细的关于这个的是 概率论 这里面有提到。
这个是强化学习的一个理论支撑,类似于梯度下降,微分对神经网络
马尔科夫链
那么首先我们的第一点是马尔可夫链:这个东西就是一系列可能发生的状态。
例如:一个人刚起床,他有可能先刷牙,然后洗脸,然后上课。
或者这个人 起床,洗澡,刷牙,然后上课。
用一条链来表示就是:
刷牙-洗脸-上课
洗澡-刷牙-上课
策略

累计回报

这个主要是看到马尔可夫链,当前的状态对后面是有关联的。
值函数

他们之间的对应关系大致如下图:
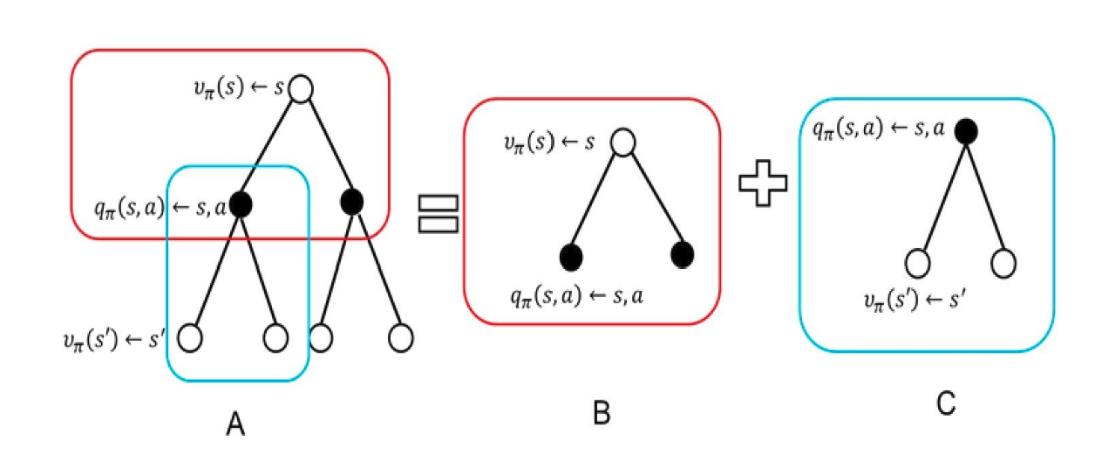
具体表现
强化学习就是数学原理是基于马尔可夫来的,那么在实际的表现当中的目的是为了求取一个表格Q。
这个表格Q,其实就是:
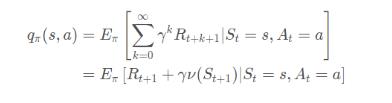
按照前面的粒子就是这个玩意:
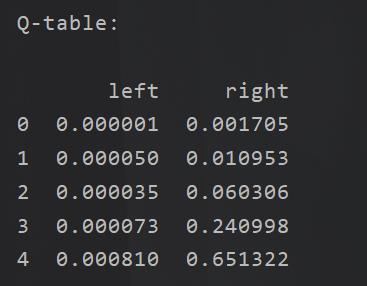
在我们实际上开始的时候Q表我们是不知道的,所以我们会有一个初始化,之后输入当前的状态和下一步的动作,会得到当前如果选择了这个动作,那么将得到的奖励,以及下一个状态,我们先通过q(s,a)可以得到。但是除此之外,由于我们实际上Q表一开始是随机的,所以是需要进行不断完善,收敛的,所以我们还需要不断更新我们的Q表。
所以在我们的实际代码里面还是有不一样的。
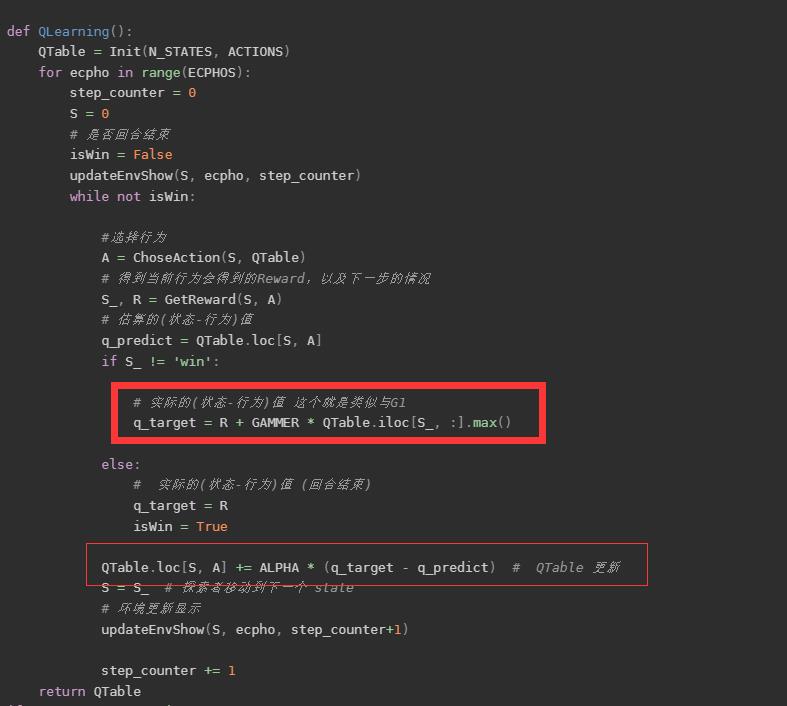
DQN神经网络
这个主要是因为论文中提到了DDPG,如果不说这个DQN 的话,这个DDPG很难说下去,那么论文也很难讲下去,这篇论文的难点在于知识面较广,实际算法其实不难。
DQN 其实和QLearn是一样的,区别在于,原来的Q表从一个表,一个有实体的表,变成了一个神经网络。目的是为了,通过神经网络去拟合那个Q表,因为在实际过程当中,如果需要将所有的状态和动作价值存起来是不可能的如果它的状态很多的话。所以需要一个神经网络来做拟合。
伪代码如下:

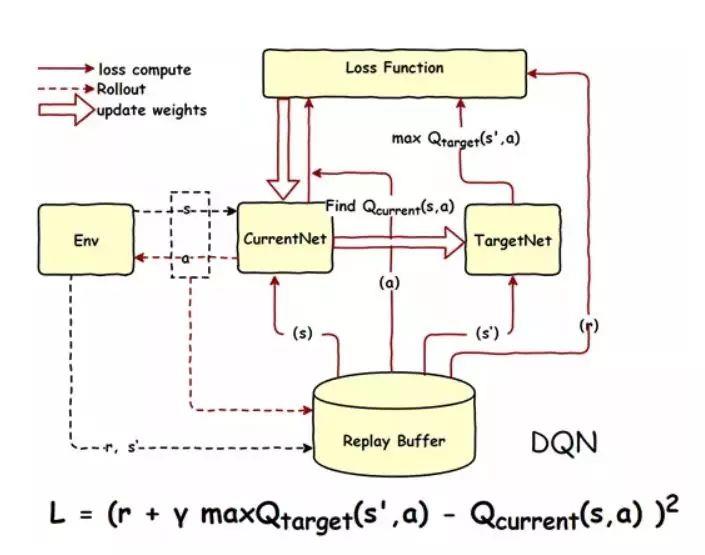
编码细节
在我们原来的时候,使用Q表
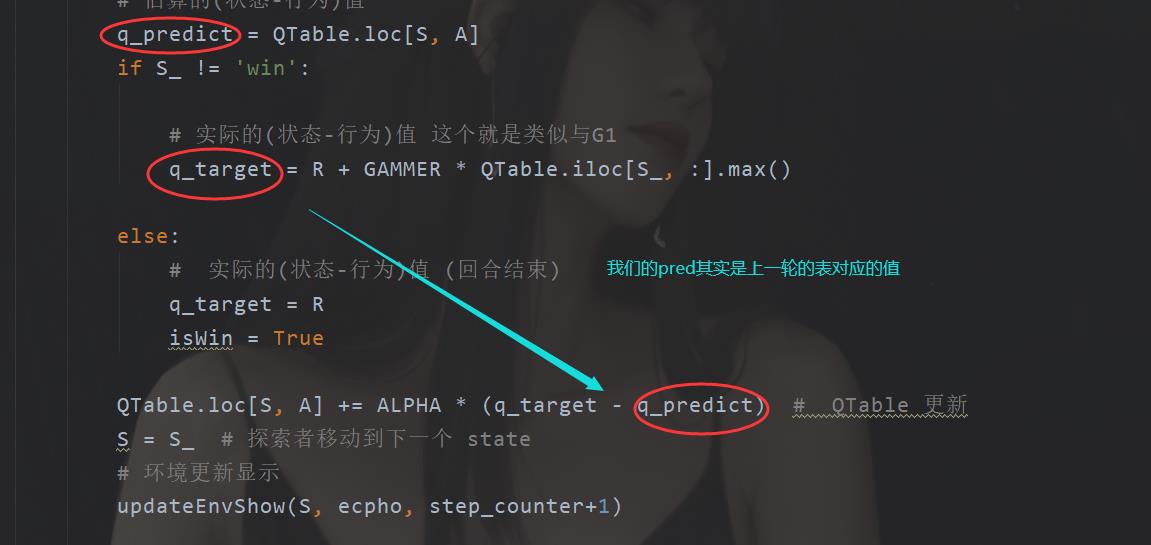
但是现在的话,由于我们是直接使用了这种“特殊的表”所以我们可以单独使用两个神经网络去分别代表实际和估计(预测)

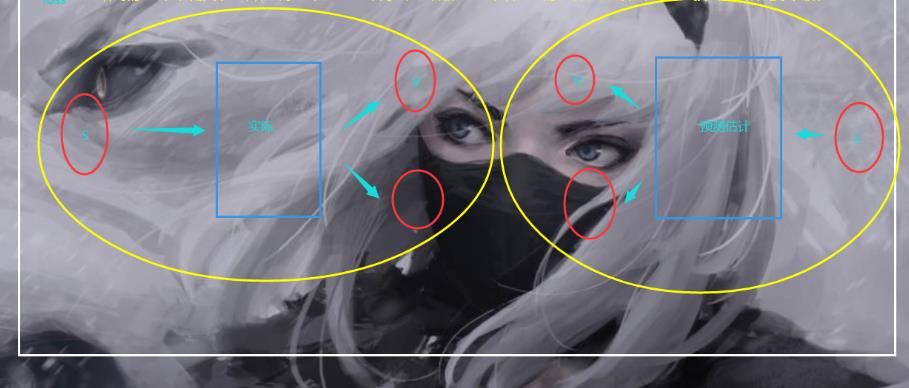
而我们的损失函数就是让q_eval 和 q_target 变小
于是:

这里的loss_func 是nn.MSELoss()
DDPG
从上面的内容,你会发现,这个玩意和传统的Qlearn没太大区别只是很巧妙地使用了神经网络,最终还是要得到一个关于每一个动作的打分,然后去按照那个得分去选择分高的动作,换一句话说是,这个神经网络还是只能得到对应动作的价值,例如 上下左右,然后选价值最大的,如 上 这个动作。
但是在我实际的PSO问题当中,我想要的是一组解,也就是你直接告诉我w c1 c2 取哪些值?
所以现在直接使用DQN 就很难了,显然这玩意貌似只能选择出一个动作,而我的w c1 c2 不可能是一个动作,如果把他看作是一个动作的话,那么你将有 无穷个动作选择,假定有范围,那就是可数无穷个动作。
为了解决那个问题,于是有了DDGP,也就是我想要直接得到一组动作,你直接告诉我 w c1 c2取得哪些值?
怎么做,没错,再来一个神经网络。
具体怎么做,如下图:
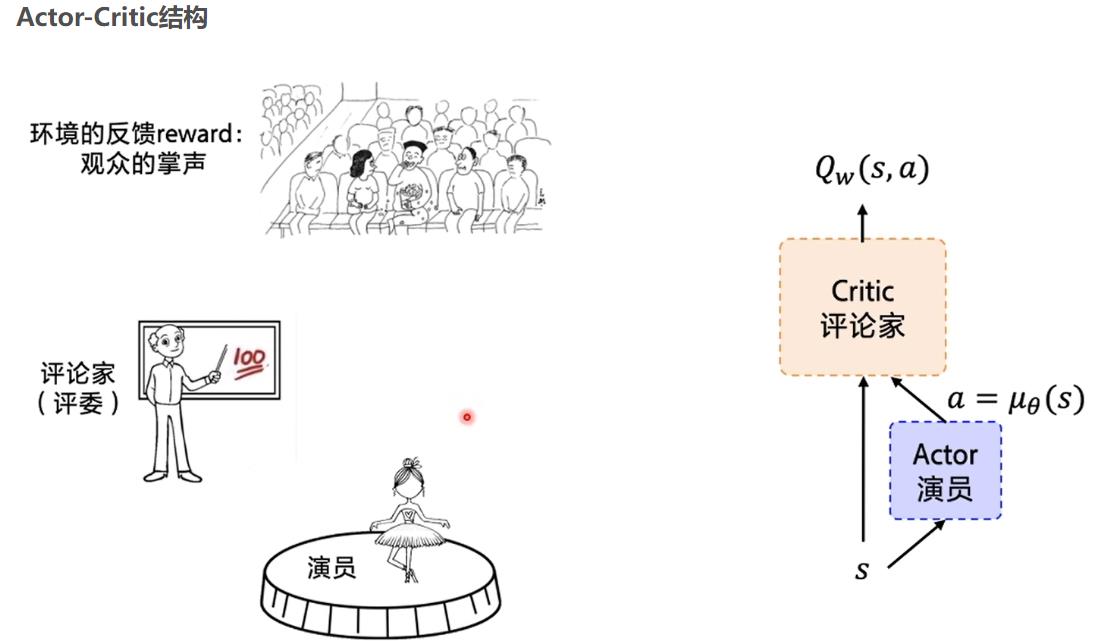
Actor 网络直接生成一个动作,然后 原来在DQN的那个网络在这里是Critic 网络 去评价,这个评价其实就是在DQN里面的那个网络,输入一个S,和 A 得到一个价值,现在这个价值变成了评分。
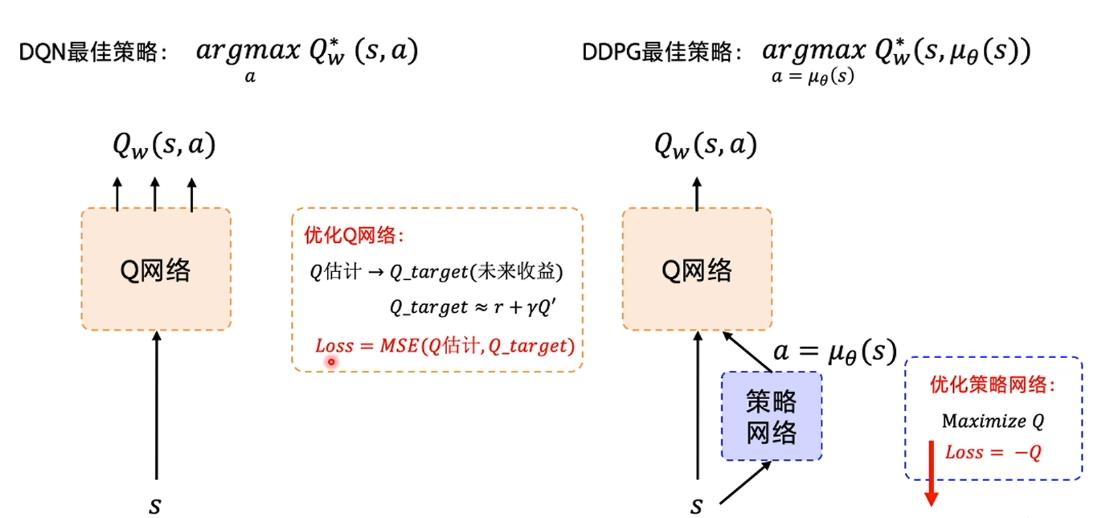
损失函数就是这样:
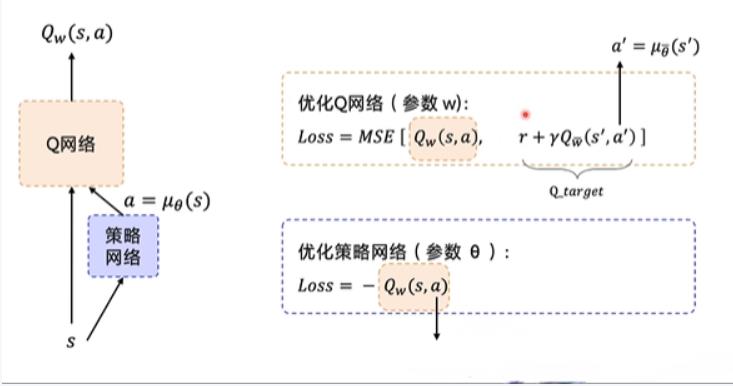
TSP模型建立
ok,随便聊了一下这个玩意(虽然我知道你一看出来了,上面的内容是copy我以前的博文的,狗头)
基本流程
首先的话,我们期望的流程是这样的:
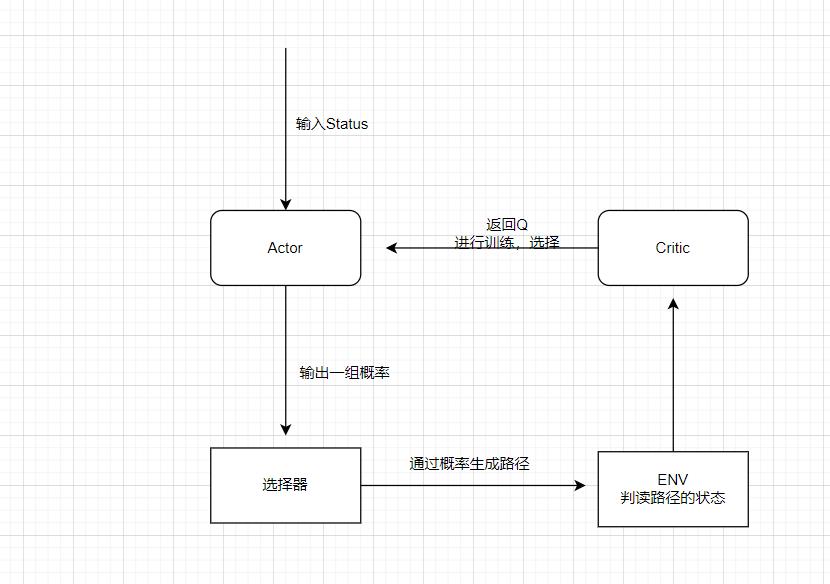
重点是说,我们期望就是这个Net可以直接输出一组概率,所以的话,我们刚好用这个DDPG。
所以的话这个是为啥用这个网络哈。
网络模型
现在的话我们需要用到这个DDPG,所以的话我们也是有两个网络的,一共是四个网络运行。这个的话,懂得都懂,实际上我们可以做到只用2个网络,而且实际上我也做到过,效果其实差不多。那么咱们的网络大概长这个样子。
Actor
这个其实没啥好说的,这个很简单的,但是优化点就在这边。
import torch
from torch import nn
import torch.nn.functional as F
class Actor(nn.Module):
"""
这个是我们的Actor网络
"""
def __init__(self,state,out):
super(Actor, self).__init__()
"""
The network structure is modified
"""
self.fc1 = nn.Linear(state,64)
self.fc1.weight.data.normal_(0, 0.1)
self.fc2 = nn.Linear(64,64)
self.fc2.weight.data.normal_(0, 0.1)
self.fc3 = nn.Linear(64,64)
self.fc3.weight.data.normal_(0,0.1)
self.out = nn.Linear(64,out)
def forward(self,x):
x = self.fc1(x)
x = F.leaky_relu(x)
x = self.fc2(x)
x = F.leaky_relu(x)
x = self.fc3(x)
x = F.leaky_relu(x)
x = self.out(x)
x = torch.tanh(x)
return x
Critic网络
这个网络的话,其实也很简单,就是多了个东西罢了。
from torch import nn
import torch.nn.functional as F
class Critic(nn.Module):
"""
这个是我们的Critic网络,因为DQN很难去直接表示三维消息
如果要就需要一个映射表,这个映射表的动作也是很复杂的,还是需要一个Net
所以的话我们这边还是直接选择使用这个DDPG
"""
def __init__(self,state_dim,action_dim):
"""
:param state_action:
"""
super(Critic,self).__init__()
self.fc1_status = nn.Linear(state_dim,64)
self.fc1_status.weight.data.normal_(0,0.1)
self.fc1_actions = nn.Linear(action_dim,64)
self.fc1_actions.weight.data.normal_(0,0.1)
self.fc2_status= nn.Linear(64,32)
self.fc2_status.weight.data.normal_(0,0.1)
self.fc2_actions = nn.Linear(64,32)
self.fc2_actions.weight.data.normal_(0,0.1)
self.fc5 = nn.Linear(32,16)
self.fc5.weight.data.normal_(0,0.1)
self.out = nn.Linear(16,1)
self.out.weight.data.normal_(0,0.1)
def forward(self,status,actions):
status = self.fc1_status(status)
status = F.leaky_relu(status)
status = self.fc2_status(status)
actions = self.fc1_actions(actions)
actions = F.leaky_relu(actions)
actions = self.fc2_actions(actions)
net = status+actions
net = F.leaky_relu(net)
net = self.fc5(net)
net = F.leaky_relu(net)
out = self.out(net)
return out
输入输出
OK,那么接下来的话,咱们就是来聊聊
说完了这个,我们来定义一下输入以及输出,我们的状态是如何输入的,我们如何从输出得到一组路径。
输入
这部分的代码在这里:
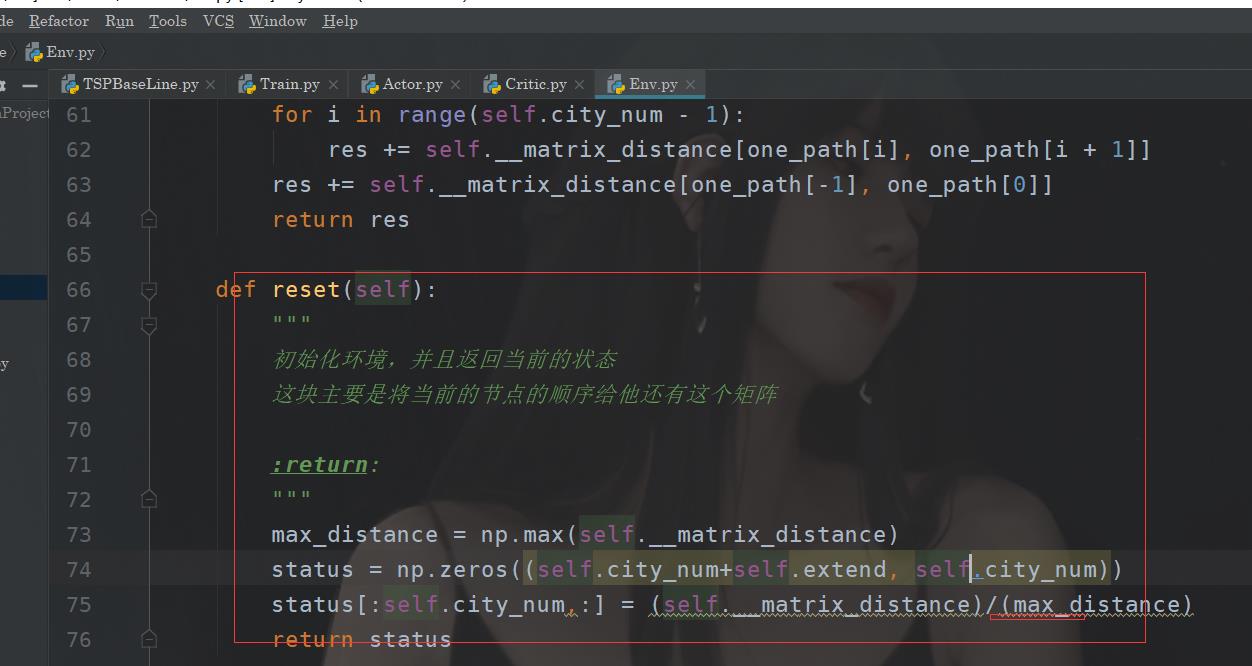
我们这边的话,我们这个还是用矩阵表示这个城市,我们输入的是城市将的一个距离矩阵,以及咱们的这个当前的较优路径(初始化的时候他们是0,当然这里其实随机生成一些很小的数会更好)。所以的值都是通过归一化处理后的。
输出
神经网络输出,这部分主要是指咱们的这个Actor网络,它输出的也是一组二维向量,得到的维度是:
(城市个数+扩充个数)x 城市个数。
之后的话通过我们的softmax可以变成一组概率,通过概率我们将生成一组路径。
具体的代码在这。
def getRoward(self,status,actions,isShow):
"""
返回当前环境的下一个动作,以及奖励。
注意status和actions都是numpy类型的
:param isShow 表示要不要输出当前最好的一个路径
:return:
"""
#计算当前下一个的状态
probabilitys = self.transform.TransProbability(actions)
#将actions,status重新转化为numpy类型
status = status.detach().numpy()
actions = actions.detach().numpy()
"""
通过概率生成我们的路径
"""
path_out = []
for probability in probabilitys:
probability /= probability.sum()
path_out.append(np.random.choice(self.city_node, (actions[0].shape), p=probability,replace=False))
fits = []
for path in path_out:
fits.append(self.comp_fit(path))
great_fits = np.argsort(fits)[:self.extend]
great_actions = actions[great_fits,:]
status[self.city_num:,:]=(great_actions)/(self.city_num-1)
#计算奖励
great_dist = fits[great_fits[0]]
R = self.tanh(self.best_dist-great_dist)
if(self.best_dist>great_dist):
self.best_dist = great_dist
self.best_path = path_out[great_fits[0]]
if(isShow):
self.out_path(self.best_path,self.best_dist)
return status,R
在这里的话,我们也是给出了这个Reward函数。
环境编写
之后的话,我们确定好了输入,输出之后,我们就可以开始编写环境了。
这个主要是强化学习部分的,将我们的TSP问题嵌入到我们的环境里面。
"""
基于TSP设计的强化学习模拟环境
"""
import numpy as np
import math
from DDPG.BaseLine.Transform import Transform
import matplotlib.pyplot as plt
class Env(object):
def __init__(self,Map,extend=0.2):
"""
:param Map: 这个Map就是我们城市的一个矩阵,是表示位置的一个矩阵
"""
self.Map = Map
self.city_num = len(self.Map)
self.__matrix_distance = self.__matrix_dis()
self.city_node = [node for node in range(self.city_num)]
self.best_dist = float("inf")
self.best_path = None
self.transform = Transform()
self.extend = int(self.city_num*extend)
self.tolerate_threshold = 0
self.tanh = math.tanh
def __matrix_dis(self):
res = np.zeros((self.city_num, self.city_num))
for i in range(self.city_num):
for j in range(i + 1, self.city_num):
res[i, j] = np.linalg.norm(self.Map[i, :] - self.Map[j, :])
res[j, i] = res[i, j]
return res
def draw_path(self,path):
## 绘制初始化的路径图
fig, ax = plt.subplots()
x = self.Map[:, 0]
y = self.Map[:, 1]
ax.scatter(x, y, linewidths=0.1)
for i, txt in enumerate(range(1, len(self.Map) + 1)):
ax.annotate(txt, (x[i], y[i]))
#获取头结点
ax.cla()
res0 = path
x0 = x[res0]
y0 = y[res0]
for i in range(len(self.Map) - 1):
plt.quiver(x0[i], y0[i], x0[i + 1] - x0[i], y0[i + 1] - y0[i], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.quiver(x0[-1], y0[-1], x0[0] - x0[-1], y0[0] - y0[-1], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.show()
plt.pause(0.1)
def comp_fit(self, one_path):
"""
计算,咱们这个路径的长度,例如A-B-C-D
:param one_path:
:return:
"""
res = 0
for i in range(self.city_num - 1):
res += self.__matrix_distance[one_path[i], one_path[i + 1]]
res += self.__matrix_distance[one_path[-1], one_path[0]]
return res
def reset(self):
"""
初始化环境,并且返回当前的状态
这块主要是将当前的节点的顺序给他还有这个矩阵
:return:
"""
max_distance = np.max(self.__matrix_distance)
status = np.zeros((self.city_num+self.extend, self.city_num))
status[:self.city_num,:] = (self.__matrix_distance)/(max_distance)
return status
def out_path(self, one_path,fitNess):
"""
输出我们的路径顺序
:param one_path:
:return:
"""
res = str(one_path[0] + 1) + '-->'
for i in range(1, self.city_num):
res += str以上是关于轻松解决TSP问题之强化学习(BaseLine)的主要内容,如果未能解决你的问题,请参考以下文章