一篇通俗易懂的平衡二叉树的旋转blog

Posted 2022-11-14 你，好

平衡二叉搜索树，又被称为AVL树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
在插入过程中难免出现不平衡的情况，而对树进行旋转就是解决不平衡最常用的方法。根据不同情况，大体分成单旋和双旋。

单旋

左单旋

当在右子树的右子树插入新节点导致右子树超长时，就需要向左单旋调整（RR）。

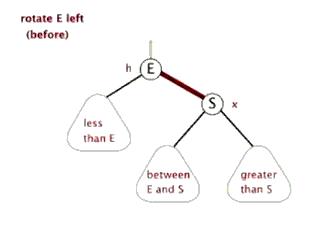
将右子树的左子树移动，变为父节点的右子树。旧的父节点作为新的父节点的左子树，同时更新高度，便完成了旋转。

• 代码

Node* rotate_RR(Node* parent)
	Node* child = parent->rightChild; 
	parent->rightChild = child->leftChild;
	child->leftChild = parent;
	parent->height = max(getHeight(parent->leftChild),getHeight(parent->rightChild)) + 1;
	child->height = max(getHeight(child->leftChild),getHeight(child->rightChild)) + 1;
	return child;

右单旋

当在左子树的左子树插入新节点导致不平衡时，就需要右单旋调整（LL）。

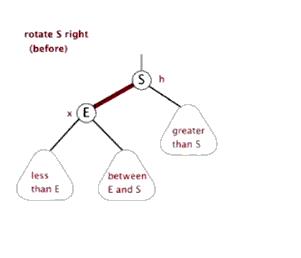
将左子树的右子树移动，变为父节点的右子树。旧的父节点作为新的父节点的右子树，同时更新高度，便完成了旋转。

• 代码

Node* rotate_LL(Node* parent)
	Node* child = parent->leftChild;
	parent->leftChild = child->rightChild;
	child->rightChild = parent;
	parent->height = max(getHeight(parent->leftChild),getHeight(parent->rightChild)) + 1;
	child->height = max(getHeight(child->leftChild),getHeight(child->rightChild)) + 1;
	return child;

双旋

先左再右

当在右子树的左子树插入新节点导致不平衡时（RL），就需要先对其右子树进行左单旋，再对其进行右单旋，同时更新高度，完成旋转。

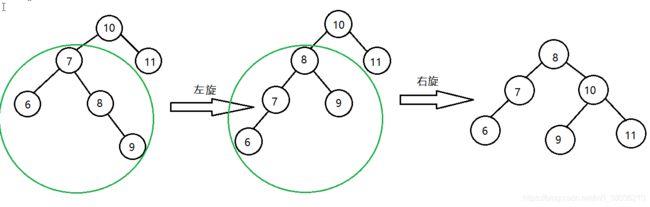
• 代码

Node* rotate_RL(Node* parent)
	Node* child = parent->rightChild;
	parent->rightChild = rotate_LL(child);
	return rotate_RR(parent);

先右再左

当在左子树的右子树插入新节点导致不平衡时（LR），就需要先对其左子树进行右单旋，再对其进行左单旋，同时更新高度，完成旋转。

• 代码

Node* rotate_LR(Node* parent)
	Node* child = parent->leftChild;
    parent->leftChild = rotate_RR(child);
    return rotate_LL(parent);