数据结构与算法分析之----各种常用排序详解
Posted 疯孑456258
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构与算法分析之----各种常用排序详解相关的知识,希望对你有一定的参考价值。
1.选择排序 思想:在需要进行排序的序列中,每次把最小(或最大)的交换到最左边的位置 案例: 待排序数组: 5 2 6 8 4 1 选择过程: 5 2 6 8 4 1 => 2 5 6 8 4 1 => 1 5 6 8 4 2 => 1 4 6 8 5 2 => 1 2 6 8 5 4 => 1 2 5 8 6 4 => 1 2 4 8 6 5... 2.冒泡排序 思想:在需要进行排序的序列中,分为未排好序的(左部分)和排好序的(右部分),每次把未排序的最后一个数推到排好序的相应位 置,因为其过程像气泡一样往上冒,故称为冒泡排序算法。 案例: 待排序数组: 2 5 6 8 4选择过程: 2 5 6 8 4 => 5 2 6 8 4 => 5 6 2 8 4 => 5 6 8 2 4 => 5 6 8 4 | 2 => 5 6 8 | 4 2 => 6 5 8 | 4 2 => 6 8 | 5 4 2 => 8 6 5 4 2
3.插入排序(两种) 思想:将待排序序列分成两部分,左边部分是排好序的,右边部分是未排序的,开始时排好序的就只有第一个元素,然后把右边 未排序的元素 一个一个插入排序到左边,直到元素全部到左边就形成了排好序的结构 3.1 直接插入 思想:在将元素插入左边排好序的序列时,通过从左到右一个一个进行比较来查找要插入的位置。 案例:5 2 6 8 4 插入过程:5 | 2 6 8 4 => 5 2 | 6 8 4 => 6 5 2 | 8 4 => 8 6 5 2 | 4 => 8 6 5 4 2 3.2 折半插入 思想:在将元素插入左边排好序的序列时,通过二分搜索的方式查找到要插入的位置。找到位置后插入的过程和直接插入一致
4.希尔排序 思想:将元素进行同余分组,比如元素个数有8个,若将其分为d1=4组,即每一个元素的下标进行模3运算,下标0,4模4余数都 为0为一组,1,5余1 为一组,2,6余2为一组,3,7余3为一组,当然这只是一种逻辑上的划分,并不是物理上对其进行 切分。然后在各组内进行直接插入排序,排序完再对其进行分组,一般取d(i+1) = ⌊d(i)/2⌋,此时的话d2=⌊d1/2⌋= 2组,就 这样一直分组排序到di = 1并插入排序结束 案例:0 6 5 8 4 2 1 9 希尔过程:



5.合并排序 思想:将待排序元素分成大小大致相同的两个子集合,分别对两个子集进行合并排序,最终将排好序的子集合并成所要求的排好 序的集合 案例:0 6 5 8 4 2 1 9 合并排序过程:0 6 5 8 | 4 2 1 9 => 0 6 | 5 8 | 4 2 | 1 9 => 0 6 | 5 8 | 2 4 | 1 9 => 0 5 6 8 | 1 2 4 9 => 0 1 2 4 5 6 8 9 code:
package cn.qunye.Sort_排序;
import java.util.ArrayList;
import java.util.List;
/**
* 合并排序:
* 将待排序元素分成大小大致相同的两个子集合,分别对两个子集进行合并排序,最终将排好序的子集合并成所要求的排好序的集合
* 时间复杂度:O(logn)
* @author qunye
* 2016/03/10
*/
class MergeSortClass<T extends Comparable>
public void MergeSort(List<T> arr,int left,int right)
List<T> arrSortTemp = new ArrayList<T>();
if(left < right) //至少两个才需要排序
int middle = (left+right)/2;
MergeSort(arr, left, middle); //左边进行排序
MergeSort(arr, middle+1, right); //右边进行排序
merge(arr, arrSortTemp,left, middle, right); //合并到集合arr
copy(arr, arrSortTemp, left, right); //复制回集合arr
arrSortTemp = null;
/**
* 合并
*/
public void merge(List<T> a,List<T> b,int left,int middle,int right)
int l = left,r = middle+1;
while((l <= middle) && (r <= right))
if(a.get(l).compareTo(a.get(r)) <= 0)
b.add(a.get(l++));
else
b.add(a.get(r++));
if(l <= middle)
for(;l<=middle;b.add(a.get(l++)));
if(r <= right)
for(;r<=right;b.add(a.get(r++)));
public void copy(List<T> a,List<T> b,int left,int right)
int index = 0;
for(int i=left;i<=right;i++)
a.set(i, b.get(index++));
/**
* 学生类
*/
class Student implements Comparable<Object>
private String stuName;
private int stuNum;
public Student(String stuName, int stuNum)
super();
this.stuName = stuName;
this.stuNum = stuNum;
public String getStuName()
return stuName;
public void setStuName(String stuName)
this.stuName = stuName;
public int getStuNum()
return stuNum;
public void setStuNum(int stuNum)
this.stuNum = stuNum;
@Override
public int compareTo(Object obj)
Student stu;
if(obj instanceof Student)
stu = (Student)obj;
else
return -1;
if(this.getStuNum() <= stu.getStuNum())
return 0;
return 1;
public class MergeSortMain
public static void main(String agrs[])
List<Student> stus = new ArrayList<Student>();
stus.add(new Student("小a",15));
stus.add(new Student("小b",18));
stus.add(new Student("小c",21));
stus.add(new Student("小d",13));
stus.add(new Student("小e",17));
stus.add(new Student("小f",19));
stus.add(new Student("小g",10));
stus.add(new Student("小h",16));
System.out.println("====================合并排序前====================");
for(Student stu : stus)
System.out.println(stu.getStuNum()+":"+stu.getStuName());
new MergeSortClass().MergeSort(stus, 0, stus.size()-1);
System.out.println("====================合并排序后====================");
for(Student stu : stus)
System.out.println(stu.getStuNum()+":"+stu.getStuName());
6.改进的合并排序 思想:先将数组中相邻的元素两两配对,构成n/2组排好序的子数组段,再合成长度为4的排好序的子数组段,如此下去 案例:0 6 5 8 4 2 1 9 合并排序过程:0 6 | 5 8 | 4 2 | 1 9 => 0 6 | 5 8 | 2 4 | 1 9 => 0 5 6 8 | 1 2 4 9 => 0 1 2 4 5 6 8 9 code:学生类的定义和main()方法同上
public void BetterMergeSort(List<T> arr)
int d = 1;
int len = arr.size();
while(d <= len)
mergePass(arr,d++,len);
private void mergePass(List<T> arr, int d,int len)
int leftIndex = 0; //需要合并的最左边下标
while(leftIndex < len)
List<T> arrSortTemp = new ArrayList<T>();
merge(arr,arrSortTemp,leftIndex,leftIndex+d-1,leftIndex+2*d-1); //合并两个子子数组段
leftIndex += 2*d; //需要合并的最左边下标指到下两个需要合并的子数组段的首位
arrSortTemp = null;
/**
* 合并
*/
public void merge(List<T> a,List<T> b,int left,int middle,int right)
int l = left,r = middle+1;
while((l <= middle) && (r <= right))
if(a.get(l).compareTo(a.get(r)) <= 0)
b.add(a.get(l++));
else
b.add(a.get(r++));
if(l <= middle)
for(;l<=middle;b.add(a.get(l++)));
if(r <= right)
for(;r<=right;b.add(a.get(r++)));
7.快速排序 思想:取第一个元数 a 作为基准元素,将数组分成三部分,比a小的元素放到一个数组里面,比a大的放到一个数组里面,再分别 对这两个数组进行快排 然后进行合并。 案例:3 6 5 8 4 2 1 9 快排过程:3 6 5 8 4 2 1 9 => 2 1 |3| 6 5 8 4 9 => 1 |2| |3| 5 4 |6| 8 9 => 1 |2| |3| 4 |5| |6| |8| 9 => 1 2 3 4 5 6 8 9 改进的快排:随机快排 思想:若对数组9 8 7 6 5 4 3 2 1进行快排,每次选取第一个元素作为基准元素,分组将很不均衡,这种极端情况将 导致时间复杂 度和简单排序一样。为避免这样的极端情况,选取一个随机数作为基准元素
code:
package cn.qunye.Sort_排序;
import java.util.Random;
/**
* 快速排序:
* 取第一个数 a 作为基准元素,将数组分成三部分,比a小的元素放到一个数组里面,比a大的放到一个数组里面,再分别对这两个数组进行快排
* 时间复杂度:O(nlogn)
* 不稳定
* 随机快排:
* 随机取一个元素作为基准元素,避免了极端的情况(比如其他元素都比第一个元素大或者小,最极端的情况会变成选择排序,复杂度为O(n^2))
* 时间复杂度:O(nlogn)
* 以下是基于随机快排实现
* @author qunye
* 2016/03/10
*/
public class QuickSort
static int sum = 0;
static int[] arr = 4,5,26,85,46,19,52,6,37,88,44,8,9,3,22,12,21,23,32,50;
private static void qSort(int left,int right)
if(left < right)
int pIndex = partition(left,right); //对数组进行划分,并返回划分的下标
System.out.println("\\n第"+(++sum)+"轮排序后");
for(int a : arr)
System.out.print(a+"、");
qSort(left,pIndex); //左边部分快排
qSort(pIndex+1, right); //右边部分快排
/**
* 对数组进行划分,并返回划分的下标
* @param left
* @param right
* @return
*/
private static int partition(int left, int right)
int baseLine = new Random().nextInt(right-left)+left; //得到随机基准元素
int baseValue = arr[baseLine];
while(true)
while(arr[left] < baseValue)
left++;
while(arr[right] > baseValue)
right--;
if(left >= right)
break;
swap(left, right);
return left;
public static void swap(int a,int b)
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
public static void main(String agrs[])
for(int a : arr)
System.out.print(a+"、");
qSort(0,arr.length-1);
8.堆排序 思想:先通过数组按层次遍历构建二叉堆,再通过二叉堆得到排序数组 先引入二叉堆的概念: 定义: 1、完全二叉树或近似完全二叉树 2、父节点的键值总是 ≥/≤ 任何一个子节点 3、每个节点的左右子树都是一个二叉堆 堆插入: 每次都是插入到最后一个位置,然后跟它的父节点比较,如果比父节点小则与父节点交换, (可以确定另一个子节点必然比原先的父节点小,所以交换之后这三个节点必然是一个合法堆), 然后就这样跟下一个父节点一直比对下去,直到比父节点小,则结束 插入示例:
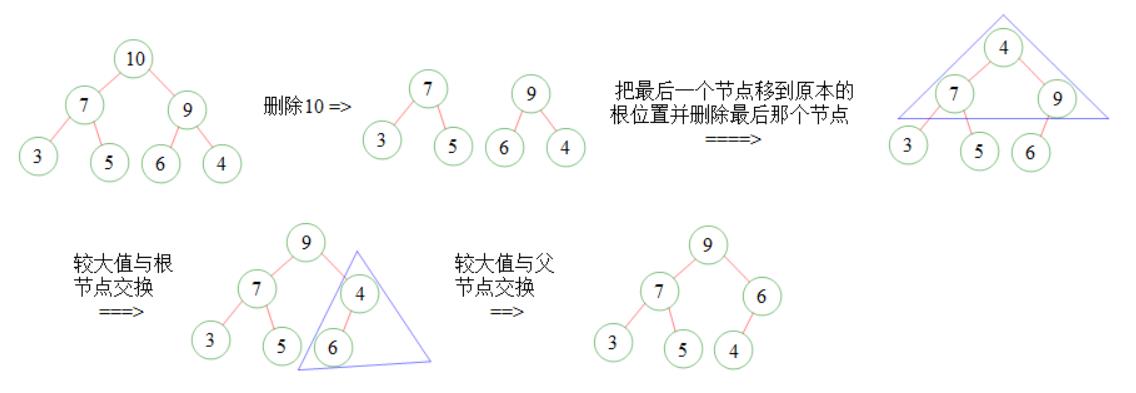
 堆删除:
每次删除的都是根节点,然后把最后一个叶节点的值赋给根节点并去掉这个叶节点,对新的二叉
树进行重建。若所有节点有比根节点小的数,则将根节点与左右节点中的较小数与根节点交换,
交换成功后这三个节点不然构成了一个合法堆,对于被交换了节点的子树,进行类似的做法,就可以
重建好二叉堆。
删除示例:
堆删除:
每次删除的都是根节点,然后把最后一个叶节点的值赋给根节点并去掉这个叶节点,对新的二叉
树进行重建。若所有节点有比根节点小的数,则将根节点与左右节点中的较小数与根节点交换,
交换成功后这三个节点不然构成了一个合法堆,对于被交换了节点的子树,进行类似的做法,就可以
重建好二叉堆。
删除示例:
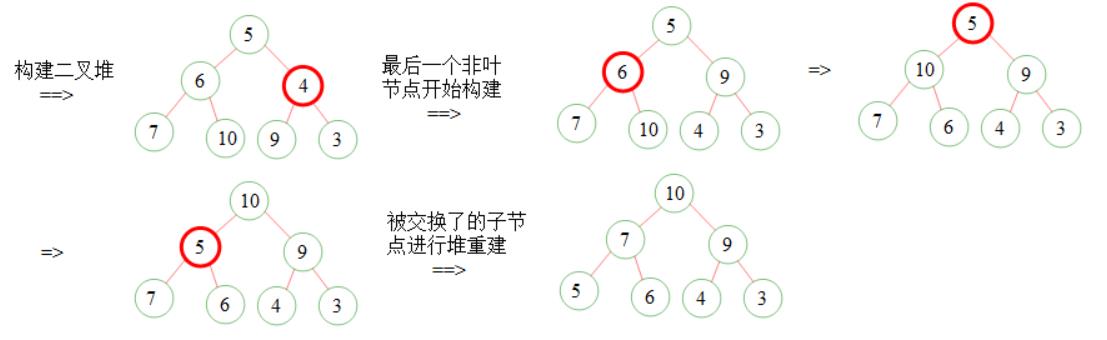
数组 -> 二叉堆:首先将数组按序组成一个完全二叉树,明显的二叉树每个叶子节点都是合法的二叉堆,从除了叶子节点的最后一个 节点 开始重建,先跟它的 左右子节点进行比较,将最小的作为父节点,则这三个节点必然可以构成一个合法堆,然 后对被交 换了的子节点所在的子树进行一次堆重建, 就像堆删除的时候那样重建,通过同样的方式处理再前一个节 点,直到根节 点完毕,就建好了二叉堆 二叉堆 -> 排序:将根节点跟数组最后一个位置(也就是最后一个节点)的值进行交换,然后将前面的 n-1个节点作为一个新的二叉树进 行重 建(其实有点像删除堆在删除了根节点之后的操作),重建好新的二叉堆之后又把根节点与数组最后第二个数的 值进行交换 ,然后又重建,知道结束就可以把二叉堆数组变成排序数组,该数组越往后越小(因为每次都是取最小堆 的根节点),所以 是个降序的排序数组
示例: 5 6 4 7 10 9 3 数组 -> 二叉堆的构建过程:
 二叉堆 -> 堆排序的过程:
二叉堆 -> 堆排序的过程:
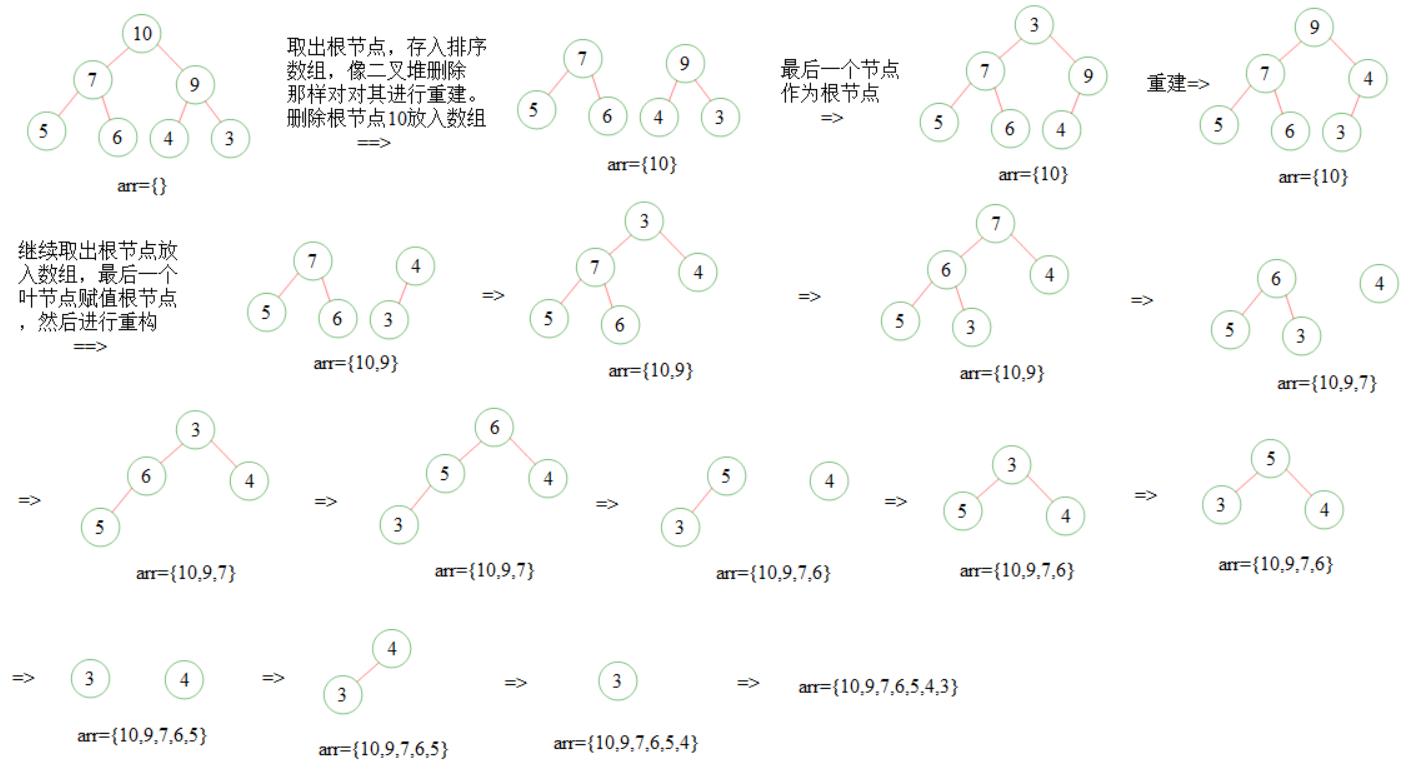
code:
package cn.qunye.Sort_排序;
/**
* 堆排序:
* 二叉堆:
* 定义:
* 1、完全二叉树或近似完全二叉树
* 2、父节点的键值总是 ≥/≤ 任何一个子节点
* 3、每个节点的左右子树都是一个二叉堆
* 堆插入:
* 每次都是插入到最后一个位置,然后跟它的父节点比较,如果比父节点小则与父节点交换,
* (可以确定另一个子节点必然比原先的父节点小,所以交换之后这三个节点必然是一个合法堆),
* 然后就这样跟下一个父节点一直比对下去,直到比父节点小,则结束
* 堆删除:
* 每次删除的都是根节点,然后把最后一个叶节点的值赋给根节点并去掉这个叶节点,对新的二叉
* 树进行重建。若所有节点有比根节点小的数,则将根节点与左右节点中的较小数与根节点交换,
* 交换成功后这三个节点不然构成了一个合法堆,对于被交换了节点的子树,进行类似的做法,就可以
* 重建好二叉堆。
* 数组->二叉堆:
* 首先将数组按序组成一个完全二叉树,明显的二叉树每个叶子节点都是合法的二叉堆,从除了叶子节点
* 的最后一个节点开始重建,先跟它的左右子节点进行比较,将最小的作为父节点,则这三个节点必然可以
* 构成一个合法堆,然后对被交换了的子节点所在的子树进行一次堆重建,就像堆删除的时候那样重建,
* 通过同样的方式处理再前一个节点,直到根节点完毕,就建好了二叉堆
* 二叉堆->堆排序:
* 将根节点跟数组最后一个位置(也就是最后一个节点)的值进行交换,然后将前面的n-1个节点作为一个新
* 的二叉树进行重建(其实有点像删除堆在删除了根节点之后的操作),重建好新的二叉堆之后又把根节点与
* 数组最后第二个数的值进行交换,然后又重建,知道结束就可以把二叉堆数组变成排序数组,该数组越往
* 后越小(因为每次都是取最小堆的根节点),所以是个降序的排序数组。
* 时间复杂度:O(nlogn)
* @author qunye
* 2016/03/10
*
*/
public class HeadSort
static int sum = 0;
static int[] arr = 4,5,26,85,46,19,52,6,37,88,44,8,9,3,22,12,21,23,32,50;
/**
* 构建二叉堆
*/
public static void buildHead(int length)
/*
* 1.找到最后一个非叶子节点
* 普及知识:
* 对于完全二叉树,设几点数为n,度为0的节点数为n0,度为1的节点数为n1,度为2的节点数为n2
* 则必然有:
* n = n0+n1+n2
* n0 = n2+1
* n0 = (n+1-n1)/2 [其中n1 = 0或1,n是奇数时为0,n为偶数时为1]
* 2.往前遍历每一个节点
*/
int len = length; //需要构建二叉堆的长度
int n1 = (len+1)%2; //度为1的节点数
int leaf = (len+1-n1)/2; //叶子节点数得出
int right = len-leaf; //需要进行对排序的节点
while(--right >= 0) //往前遍历,构建二叉堆
Head(right,len);
public static void Head(int right,int len)
int min = arr[right];
int l = right*2+1; //左
int r = right*2+2; //右节点
if(l < len) //左节点存在(对完全二叉树来说,无左节点比如没有右节点,故只存在右节点的情况无需考虑)
if(r < len) //右节点存在
if(arr[l] < arr[r])
if(arr[l] < min)
swap(l, right);
Head(l,len);
else
if(arr[r] < min)
swap(r, right);
Head(r,len);
else
if(arr[l] < min)
swap(l, right);
Head(l,len);
/**
* 二叉堆-->堆排序
*/
public static void Head2Sort(int length)
int index = -1;
while(++index < length-1)
buildHead(length-index);
swap(0, length-index-1);
System.out.println("\\n第"+(++sum)+"轮后");
for(int temp : arr)
System.out.print(temp+"、");
public static void swap(int a,int b)
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
public static void main(String agrs[])
Head2Sort(arr.length);
下一章将详解数据结构与算法的各种树,敬请关注本博客 旨在从简单易懂的角度介绍,若有什么错误请指出,谢谢各位。
以上是关于数据结构与算法分析之----各种常用排序详解的主要内容,如果未能解决你的问题,请参考以下文章