刷题精选：力扣565.数组嵌套

Posted 2022-11-03 bit_zhy

刷题精选：力扣565.数组嵌套

• 题目描述
• 算法分析
• 代码分析

题目描述

索引从0开始长度为N的数组A，包含0到N - 1的所有整数。找到最大的集合S并返回其大小，其中 S[i] = A[i], A[A[i]], A[A[A[i]]], … 且遵守以下的规则。

假设选择索引为i的元素A[i]为S的第一个元素，S的下一个元素应该是A[A[i]]，之后是A[A[A[i]]]… 以此类推，不断添加直到S出现重复的元素。

示例 1:

输入: A = [5,4,0,3,1,6,2]
输出: 4
解释:
A[0] = 5, A[1] = 4, A[2] = 0, A[3] = 3, A[4] = 1, A[5] = 6, A[6] = 2.

其中一种最长的 S[K]:
S[0] = A[0], A[5], A[6], A[2] = 5, 6, 2, 0

提示：

1.N是[1, 20,000]之间的整数。
2.A中不含有重复的元素。
3.A中的元素大小在[0, N-1]之间。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/array-nesting
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

算法分析

这个题其实最关键点有两点：
1.题目中说数组A之中的数字元素大小在[0 , N-1]之间
这一条件说明了，我们的元素大小都在这个元素能够覆盖的下标之内，那么我们以下标所对应的元素作为下一个访问下标，总能访问回来，形成一个环，最复杂的情况就是数组是一个不完全的递增数组，开头元素是1，这时需要遍历一遍数组才能得到完整的环，举个例子：数组为 下标对应在数组下边
数组元素：1，2，3，4，5，6，0
数组下标：0，1，2，3，4，5，6
那么我们以0下标开始访问，0中元素为1，下一个访问下标1，1中元素为2，下一个访问2下标，不断重复，直到最后一个6下标元素为0，形成一个环，大小为数组大小，这种情况是环最长的，那么如果数组元素乱序排列，可能形成环更容易，例如题目中给的示例1：A = [5,4,0,3,1,6,2]
0下标形成的环是

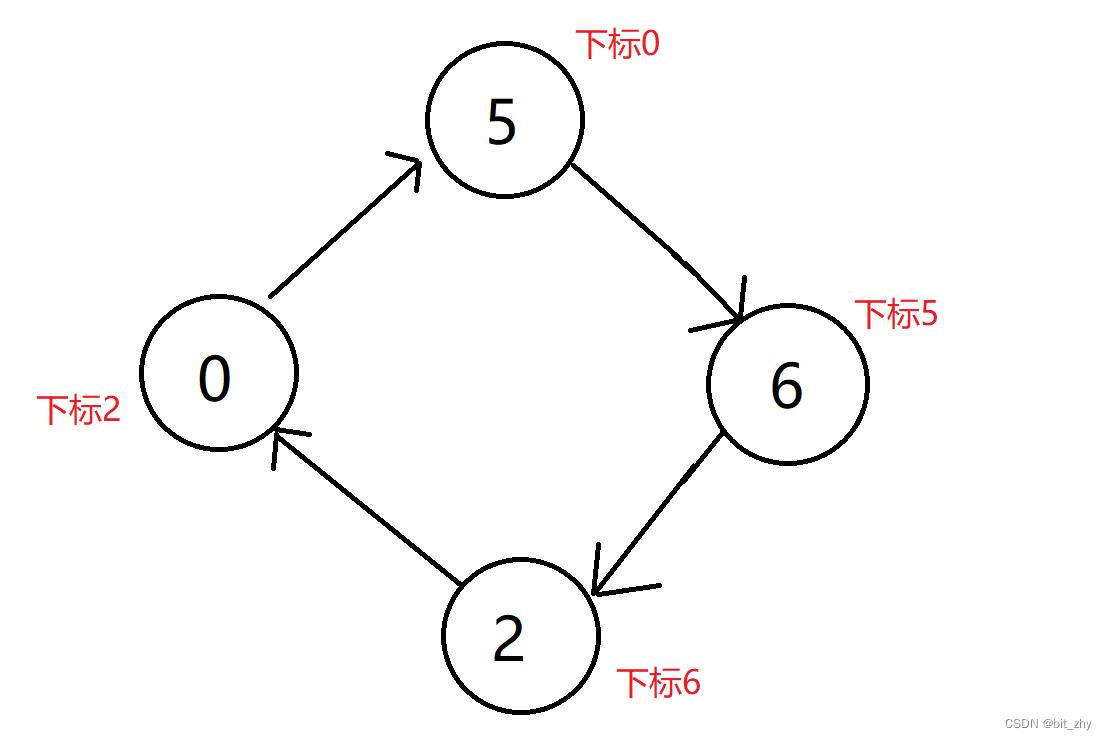
我们还需要理解，从这个环的中的任意一个点为开头，那么形成的环一定是和这个环一样的，例如从6下标开始形成的环是2 -> 0 -> 5 -> 6，那么我们就能确定，只要曾经访问过的环中出现过的元素，就不需要再作为下一个环的开头下标访问一次了，因为形成的环是一样的，长度也是一样的，例如上述中，以5，6，2作为开头下标的环就没必要再访问一次了。
2.A中不存在重复的元素
这句话意味着每一个环都是单独的，不可能是交叉的，因为每个元素只会出现一次，那么不可能有两个相同的元素对应相同的下标导致某一个环中的某一元素被两个箭头指向，再结合1中的结论，我们只需要将访问过的环中所有的元素做一个标记，下次访问新环的时候，如果开头元素是被标记过的就没必要访问这个环了。

代码分析

class Solution 
    public int arrayNesting(int[] nums) 
        //定义一个最长的数字作为返回
        int finallynumber = 0;
        //循环遍历每一个下标所对应的环
        for(int i = 0; i < nums.length; i++)
            int count = i;
            int total = 0;
            //将访问过的元素标记为-1后，下一个环的开始元素若是-1
            //那说明形成的环是之前形成过的，不需要计算，只计算不是-1的
            while(nums[count] != -1)
                total++;
                int next = nums[count];
                //将-1作为标记，访问过的元素就改为-1
                nums[count] = -1;
                count = next;
            
            if(finallynumber <= total)
                finallynumber = total;
            
        
        return finallynumber;