最优化理论·非线性最小二乘
Posted tina_ttl
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最优化理论·非线性最小二乘相关的知识,希望对你有一定的参考价值。
最优化理论·非线性最小二乘
标签(空格分隔): 数学
非线性最小二乘问题是椭圆拟合中最易遇到的优化问题,本文主要对非线性二乘的基本分析做简单介绍
1. 什么是最小二乘问题
目标函数能够写为m个函数平方和的优化问题
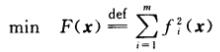
其中,每个函数 f i ( x ) f_i(x) fi(x)都是待优化向量 x x x的函数。
2.非线性最小二乘问题
- 当 f i ( x ) f_i(x) fi(x)是关于 x x x的非线性函数时,即为非线性优化问题
- 此时,需要利用Taylor一阶展开近似 f i ( x ) f_i(x) fi(x)
2.1 f i ( x ) f_i(x) fi(x)的一阶近似
-
设 x ( k ) x^(k) x(k)是解 x x x的第k次近似,在此处将 f i ( x ) f_i(x) fi(x)进行一阶展开,并令一阶展开值为 φ i ( x ) \\varphi_i(x) φi(x)
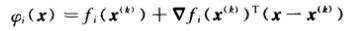
-
对上式进行整理,得到
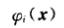
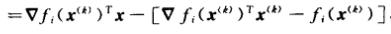
-
可以看到,一阶近似 φ i ( x ) \\varphi_i(x) φi(x)是关于待优化向量 x x x的线性函数:
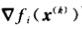
是 f i ( x ) f_i(x) fi(x)的梯度【 f i ( x ) f_i(x) fi(x)对向量x求导】在 x ( k ) x^(k) x(k)处的取值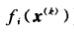
是 f i ( x ) f_i(x) fi(x)在 x ( k ) x^(k) x(k)处的取值
2.2 F(x)的近似
在得到
f
i
(
x
)
f_i(x)
fi(x)的一阶近似后,便可以计算得到F(x)的一阶近似,该一阶近似为
Φ
(
x
)
\\Phi(x)
Φ(x):
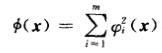

2.3 分析 Φ ( x ) \\Phi(x) Φ(x)的具体形式
-
将平方和形式写为行向量、列向量乘积形式
Φ ( x ) = [ φ 1 ( x ) , φ 2 ( x ) , ⋯ φ m ( x ) ] ⋅ [ φ 1 ( x ) φ 2 ( x ) … φ m ( x ) ] \\Phi(x) = \\left [ \\varphi_1(x),\\varphi_2(x),\\cdots\\,\\varphi_m(x) \\right ] \\cdot \\beginbmatrix \\varphi_1(x)\\\\ \\varphi_2(x)\\\\ \\dots\\\\ \\varphi_m(x) \\endbmatrix Φ(x)=[φ1(x),φ2(x),⋯φm(x)]⋅⎣⎢⎢⎡φ1(x)φ2(x)…φm(x)⎦⎥⎥⎤ -
将 φ i ( x ) \\varphi_i(x) φi(x)的具体形式代入
[ φ 1 ( x ) φ 1 ( x ) … φ 1 ( x ) ] = [ ▽ f 1 ( x ( k ) ) T ⋅ x − [ ▽ f 1 ( x ( k ) ) T − f 1 ( x ( k ) ) ] ▽ f 2 ( x ( k ) ) T ⋅ x − [ ▽ f 2 ( x ( k ) ) T − f 2 ( x ( k ) ) ] … ▽ f m ( x ( k ) ) T ⋅ x − [ ▽ f m ( x ( k ) ) T − f m ( x ( k ) ) ] ] \\beginbmatrix \\varphi_1(x)\\\\ \\varphi_1(x)\\\\ \\dots\\\\ \\varphi_1(x) \\endbmatrix = \\beginbmatrix \\ \\bigtriangledown f_1(x^(k))^T \\cdot x-\\left [ \\bigtriangledown f_1(x^(k))^T -f_1(x^(k))\\right ]\\\\ \\ \\bigtriangledown f_2(x^(k))^T \\cdot x-\\left [ \\bigtriangledown f_2(x^(k))^T -f_2(x^(k))\\right ]\\\\ \\dots\\\\ \\ \\bigtriangledown f_m(x^(k))^T \\cdot x-\\left [ \\bigtriangledown f_m(x^(k))^T -f_m(x^(k))\\right ]\\\\ \\endbmatrix ⎣⎢⎢⎡φ1(x)φ1(x)…φ1(x)⎦⎥⎥⎤=⎣⎢⎢⎡ ▽f1(x(k))T⋅x−[▽f1(x(k))T−f1(x(k))] ▽f2(x(k))T⋅x−[▽f2(x(k))T−f2(x(k))]… ▽fm(x(k))T⋅x−[▽fm(x(k))以上是关于最优化理论·非线性最小二乘的主要内容,如果未能解决你的问题,请参考以下文章