牛顿迭代法实例
Posted 统计学小王子
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了牛顿迭代法实例相关的知识,希望对你有一定的参考价值。
目录
引言
之前写过部分关于牛顿迭代的练习代码,今天分享一下。
1、理论说明
随机变量 X X X服从如下威布尔分布,密度函数满足如下的定义:
f
(
x
;
λ
,
α
)
=
λ
α
x
α
−
1
exp
−
λ
x
α
I
x
≥
0
.
f\\left( x;\\lambda ,\\alpha \\right) = \\lambda \\alpha x^\\alpha - 1\\exp \\left\\ - \\lambda x^\\alpha \\right\\I\\left\\ x \\ge 0 \\right\\.
f(x;λ,α)=λαxα−1exp−λxαIx≥0.
有样本
X
1
,
X
2
,
.
.
.
,
X
n
X_1,X_2,...,X_n
X1,X2,...,Xn,则关于样本的对数似然函数如下:
L
(
λ
,
α
)
=
n
log
(
λ
α
)
−
λ
∑
i
=
1
n
x
i
α
+
α
∑
i
=
1
n
log
(
x
i
)
+
C
.
L\\left( \\lambda ,\\alpha \\right) = n\\log \\left( \\lambda \\alpha \\right) - \\lambda \\sum\\limits_i = 1^n x_i^\\alpha + \\alpha \\sum\\limits_i = 1^n \\log \\left( x_i \\right) + C.
L(λ,α)=nlog(λα)−λi=1∑nxiα+αi=1∑nlog(xi)+C.
似然函数参数的梯度为:
L
˙
=
(
∂
L
(
λ
,
α
)
∂
λ
,
∂
L
(
λ
,
α
)
∂
α
)
,
\\dot L = \\left( \\frac\\partial L\\left( \\lambda ,\\alpha \\right)\\partial \\lambda ,\\frac\\partial L\\left( \\lambda ,\\alpha \\right)\\partial \\alpha \\right),
L˙=(∂λ∂L(λ,α),∂α∂L(λ,α)),
其中:
∂
L
(
λ
,
α
)
∂
λ
=
n
λ
−
∑
i
=
1
n
x
i
α
,
∂
L
(
λ
,
α
)
∂
α
=
n
α
+
∑
i
=
1
n
log
(
x
i
)
−
λ
∑
i
=
1
n
x
i
α
log
(
x
i
)
.
\\beginarrayl \\frac\\partial L\\left( \\lambda ,\\alpha \\right)\\partial \\lambda = \\fracn\\lambda - \\sum\\limits_i = 1^n x_i^\\alpha ,\\\\ \\frac\\partial L\\left( \\lambda ,\\alpha \\right)\\partial \\alpha = \\fracn\\alpha + \\sum\\limits_i = 1^n \\log \\left( x_i \\right) - \\lambda \\sum\\limits_i = 1^n x_i^\\alpha \\log \\left( x_i \\right) . \\endarray
∂λ∂L(λ,α)=λn−i=1∑nxiα,∂α∂L(λ,α)=αn+i=1∑nlog(xi)−λi=1∑nxiαlog(xi).
似然函数参数的黑塞矩阵为:
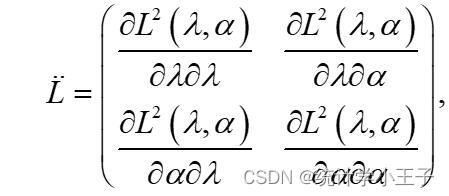
其中:
∂ L 2 ( λ , α ) ∂ λ ∂ λ = − n λ 2 , ∂ L 2 ( λ , α ) ∂ λ ∂ α = − ∑ i = 1 n x i α log ( x i ) , ∂ L 2 ( λ , α ) ∂ α ∂ λ = − ∑ i = 1 n x i α log ( x i ) , ∂ L 2 ( λ , α ) ∂ α ∂ α = − n α 2 − λ ∑ i = 1 n x i α log 2 ( x i ) . \\beginarrayl \\frac\\partial L^2\\left( \\lambda ,\\alpha \\right)\\partial \\lambda \\partial \\lambda = - \\fracn\\lambda ^2,\\\\ \\frac\\partial L^2\\left( \\lambda ,\\alpha \\right)\\partial \\lambda \\partial \\alpha = - \\sum\\limits_i = 1^n x_i^\\alpha \\log \\left( x_i \\right) ,\\\\ \\frac\\partial L^2\\left( \\lambda ,\\alpha \\right)\\partial \\alpha \\partial \\lambda = - \\sum\\limits_i = 1^n x_i^\\alpha \\log \\left( x_i \\right) ,\\\\ \\frac\\partial L^2\\left( \\lambda ,\\alpha \\right)\\partial \\alpha \\partial \\alpha = - \\fracn\\alpha ^2 - \\lambda \\sum\\limits_i = 1^n x_i^\\alpha \\log ^2\\left( x_i \\right) . \\endarray ∂λ∂λ∂L2(λ,α)=−λ2n,∂λ∂α∂L2(λ,α)=−i=1∑nxiαlog(xi),∂α∂λ∂L2(λ,α)=−i=1∑nxiαlog(xi),∂α∂α