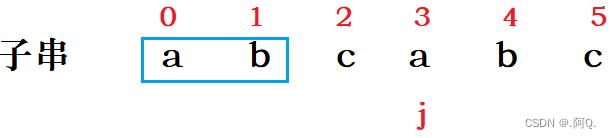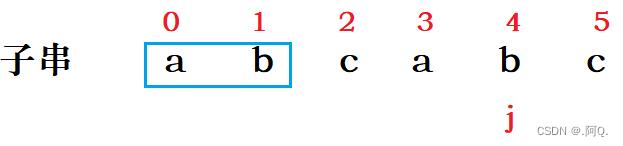[数据结构]KMP算法

Posted 2022-10-20 .阿Q.

目录

1、暴力匹配（BF）算法

2、KMP算法

next数组（手动求，方便求解题目）

值得思考的两点

注意：日常数据结构题目问next数组的值，需要在此方法求出next基础上，全部加1

next数组（公式求，方便书写代码）

3、KMP算法优化（优化next数组）

next数组优化规则

---

1、暴力匹配（BF）算法

BF算法，即暴力 (Brute Force) 算法，是普通的模式匹配算法。

BF算法的思想就是将 子串S 的第1个字符与 主串T 的第1个字符进行匹配，若相等，则继续比较S的第2个字符和T的第2个字符；若不相等，则比较S的第1个字符和T的第二个字符。依次比较下去，直到得出最后的匹配结果。BF算法是一 种蛮力算法。

例子，详细解释：

---

#include<stdio.h>
#include<string.h>

/*
字符串匹配算法 BF
str：主串
sub：子串
返回值：返回子串在主串当中的下标。如果不存在，则返回-1
*/
int BF(char *str, char *sub)

	if (str == NULL || sub == NULL)
		return -1;
	
	int lenStr = strlen(str);
	int lenSub = strlen(sub);
	int i = 0;
	int j = 0;

	while (i < lenStr && j < lenSub)
	
		if (str[i] == sub[j])
		
			i++;
			j++;
		
		else
		
			i = i - j + 1;
			j = 0;
		
	

	//执行到这说明，主串和子串肯定存在有执行完的情况
	if (j >= lenSub)//说明子串执行完
	
		return i - j;
	
	return -1;


int main()

	printf("%d\\n", BF("ababcfabcde", "abcd"));//6
	printf("%d\\n", BF("ababcfabcde", "abef"));//-1
	printf("%d\\n", BF("ababcfabcde", "ab"));//0

	return 0;

2、KMP算法

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth, J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特一莫里斯一普拉特操作(简称KMP算法)。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next函数实现，函数本身包含了模式串的局部匹配信息。

KMP算法的时间复杂度O(m+n)

区别：KMP和BF唯一不一样的地方在，我主串的 i 并不会回退，并且 j 也不会移动到0号位置（目的）

具体例子解释：

此时str[i] != sub[j]，那么怎么办呢？ （BF算法是此时 j 移动到 0 位置，i 移动到原下标的下一个位置，KMP算法该怎么做呢？）

我们发现，BF算法效率太低了（因为，i 移动到原下标的下一个位置，该位置的数是b，明显和子串a不符啊，所以产生一个优化的雏形：① i 回退位置是否能更高效？）。

由于此时 i 前面走过的元素，我们是已经知道了他们具体是哪些字符，而不再是未知区域。所以，我们能否 ② 利用好这块已知的区域？ -------->  产生KMP算法

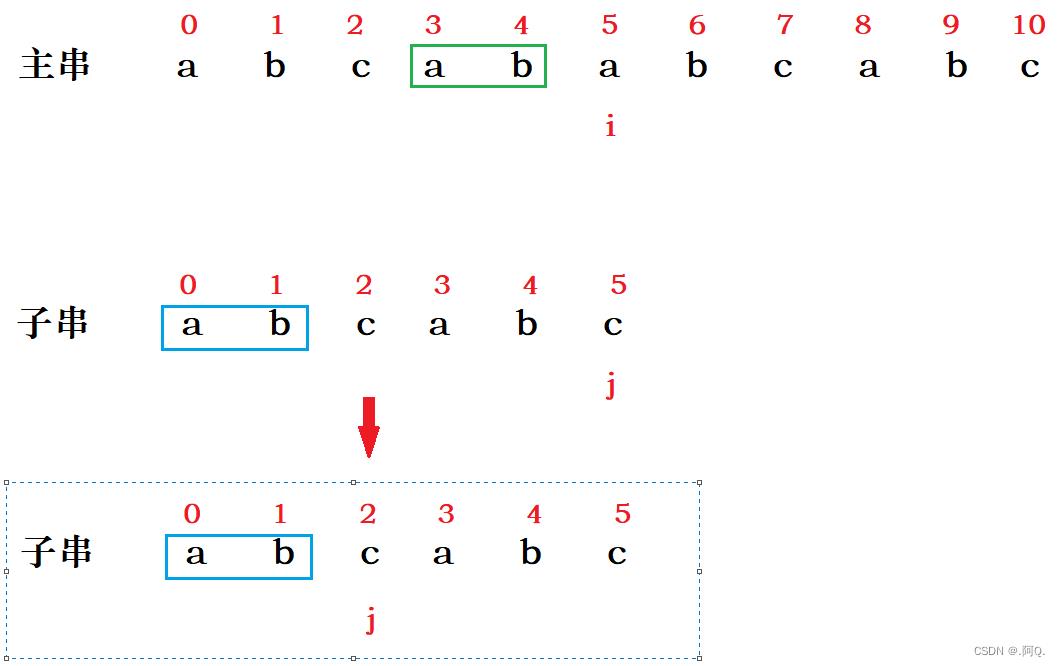
可以发现，i 前面有a  b ，是和子串中a   b 是一致的，那能否 i 不动， j 移动到2位置呢？  这样不就可以了吗省去不必要的比较了吗？

-------->  产生KMP算法思想：    i 不回退，j 回退到一个特定的位置    

所以，现在产生又一个疑问：  j 应该如何确定回退的位置呢?    先不急解决这个问题，在此之前，理理上述思路：

本身 i 是不会回退的，所以，我们尽量在主串中找到和子串匹配的那部分串。

一旦str[i] != sub[j]，那么 j 就会回退到相应位置

可以发现，j 回退到相应位置，是需要特别标识记录的，那么就产生了一个KMP算法中的核心数组： next数组

next数组（手动求，方便求解题目）

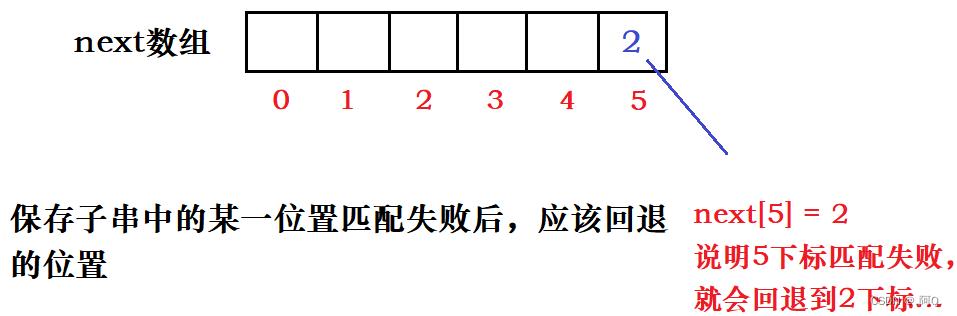
作用：保存子串中的某个位置匹配失败后，应该回退的位置。

---

next数组

1. 规则：找到匹配成功部分的两个相等的真子串（不包含本身），一个以下标0字符开始，另一个以 j-1 下标字符结尾。
2. 不管什么数据，next[0] = -1；  next[1] = 0；  在这里，我们以下标来开始，而说到第几个第几个是从1开始。

---

 

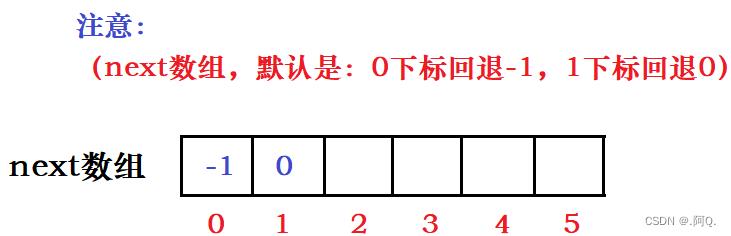
next数组的作用清楚了，那么回到最初的遗留问题：  j 应该如何确定回退的位置呢? 

找法演示，验证规则（记~）

=======================================================================================

规则： 找到匹配成功部分的两个相等的真子串（不包含本身），一个以下标0字符开始，另一个以 j-1 下标字符结尾。

=======================================================================================

此时 j 回退到2位置，2位置若和主串不匹配应该回退到哪？

====>

----------------------------------------------------
要找以sub[0]开始，
以sub[j-1]结尾的字符串，

在sub[0]~sub[j-1]中是否存在两个及以上？

----------------------------------------------------

• 如果至少存在两个，那么回退的位置数就为所有符合条件的字符串，最长字符串的长度
• 如果就存在一个，那么回退位置为0；

-----------------------------------------------------

即：a开始，b结尾的字符串在sub[0]~sub[j-1]中是否存在2个？

可以发现只有1个，那么next数组中2位置回退位置就为0；

----

那么next数组中的3位置应该回退到哪呢？

和上面一样的推理过程：

找以sub[0]开始，以sub[j-1]结尾的字符串在sub[0]~sub[j-1]中是否存在两个及以上？

即：a开始，c结尾的字符串在sub[0]~sub[j-1]中是否存在2个？

可以发现只有1个，那么next数组中3位置回退位置就为0；

----

那么next数组中的4位置应该回退到哪呢？

......找以a开始，以a结尾的字符串在sub[0]~sub[j-1]中是否存在2个？

可以发现，sub[0]~sub[0]、sub[3]~sub[3]是符合以a开始，以a结尾的字符串的，所以，存在两个字符串，那么回退的位置数就为字符串长度1（注意：sub[0]~sub[3]确实也是以a开始，以a结尾的字符串，但是只存在一个这样的串，不符合要求。所以，符合条件的字符串只有sub[0]~sub[0]、sub[3]~sub[3]，其长度就为最长字符串长度）【体会！】

----

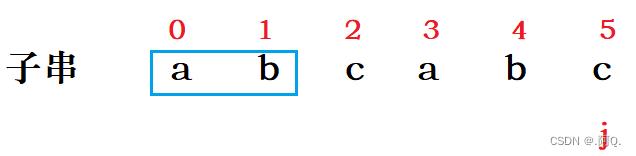
那么next数组中的5位置应该回退到哪呢？

....找以a开始，以b结尾的字符串在sub[0]~sub[j-1]中是否存在2个？

可以发现，sub[0]~sub[1]、sub[3]~sub[4]是符合以a开始，以b结尾的字符串的，所以，存在两个字符串，那么回退的位置数就为字符串长度2

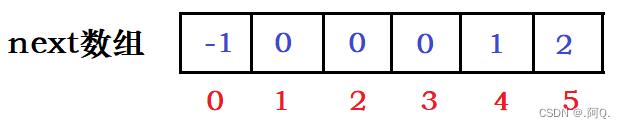
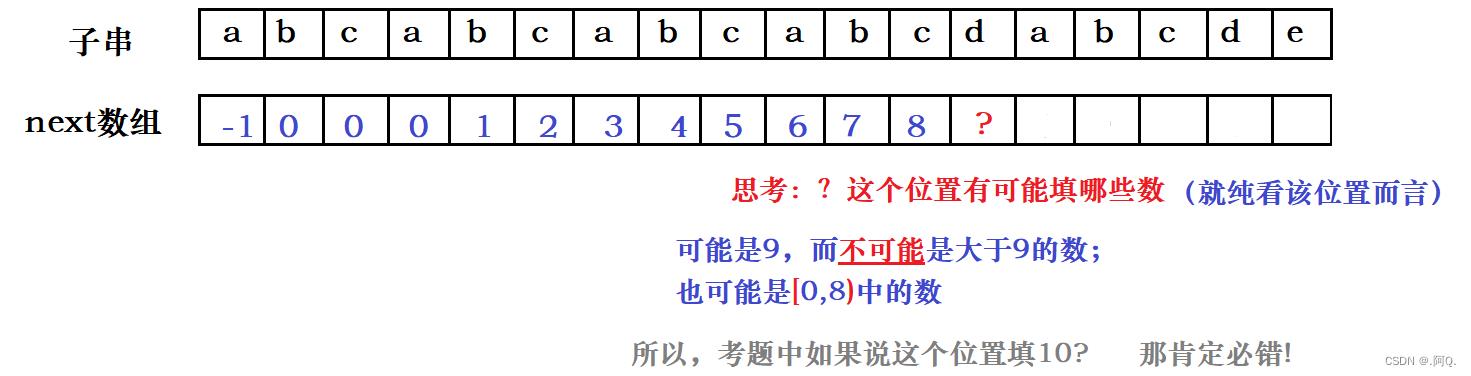
所以最终next数组为：

练习：

1. 对"  ababcabcdabcde  "，求其的next数组
2. 对"  abcabcabcabcdabcde  "，求其的next数组

答案：

--------------------------------------------------------------------------------------------------------------------

值得思考的两点

 1.

2.

注意：日常数据结构题目问next数组的值，需要在此方法求出next基础上，全部加1

---

OK，到目前为止，KMP算法中我们知道了KMP算法的思想、为什么使用next数组(next数组的作用)、next数组的手动求法

那么在代码中怎么体现这种手动算的next数组呢？----->  手算的这种方式在代码中的确不好实现（“  剪不断，理还乱  ”）。写代码，next数组需要用公式求！

---

next数组（公式求，方便书写代码）

公式求，才能方便代码书写。

起始位置next[0] = -1;   next[1] = 0;     那么知道了当前位置 i 处 next[i] = k;       如何通过当前 i 位置求出 i+1 位置呢？   （  next[i+1] = ?  ）

---

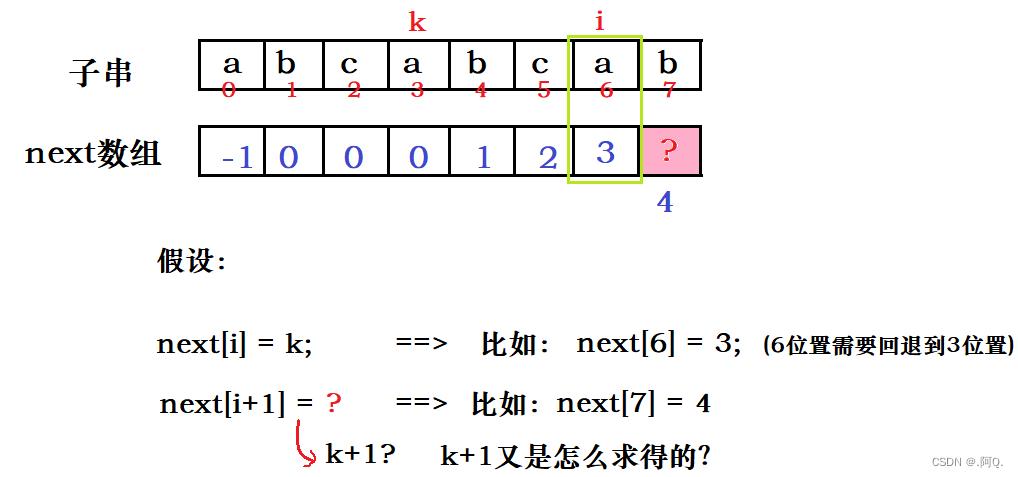
代码实现

找漏补缺版本

//找漏补缺版本
//还没实现GetNext
#include<stdio.h>
#include<string.h>
#include<assert.h>
/*
KMP算法
str：主串
sub：子串
pos: 从子串的pos位置开始匹配
return：返回子串在主串当中的下标。如果不存在，则返回-1
*/
int KMP(char* str, char* sub, int pos)

	assert(str != NULL && sub != NULL);
	int lenStr = strlen(str);
	int lenSub = strlen(sub);
	if (lenStr == 0 || lenSub == 0) return -1;
	if (pos < 0 || pos >= lenStr) return -1;

	//next数组
	int* next = (int*)malloc(sizeof(int) * lenSub);
	GetNext(sub, next);

	int i = pos;//遍历主串
	int j = 0;//遍历子串

	while (i < lenStr && j < lenSub)
	
		if (str[i] == sub[j])
		
			i++;
			j++;
		
		//一旦不匹配，就要使用到next数组来制定j的回退位置
		else
		
			j = next[j];
		
	

	//执行到这说明，主串和子串肯定存在有执行完的情况
	if (j >= lenSub)//说明子串执行完
	
		return i - j;
	
	return -1;

上述代码问题：

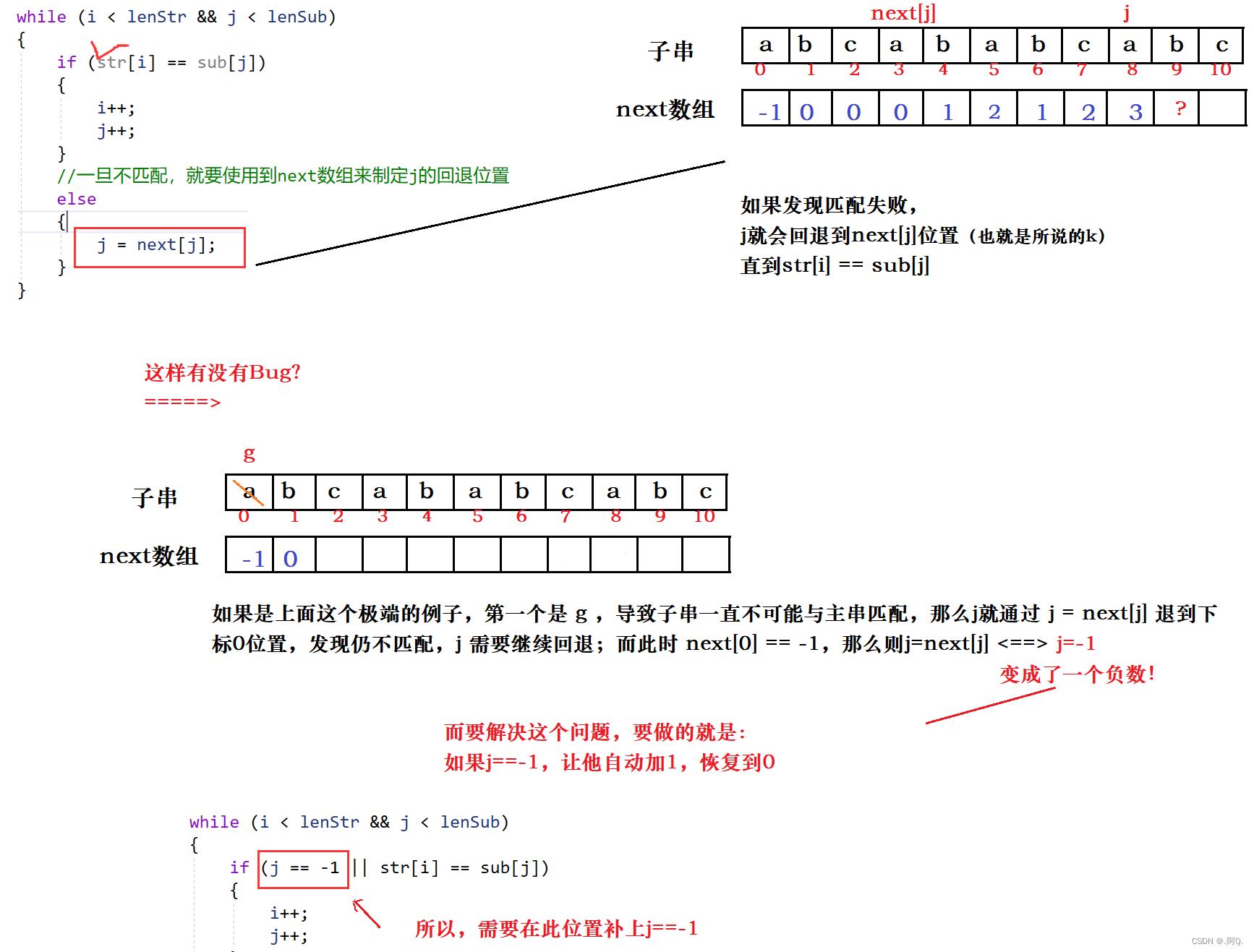
GetNext怎么实现？

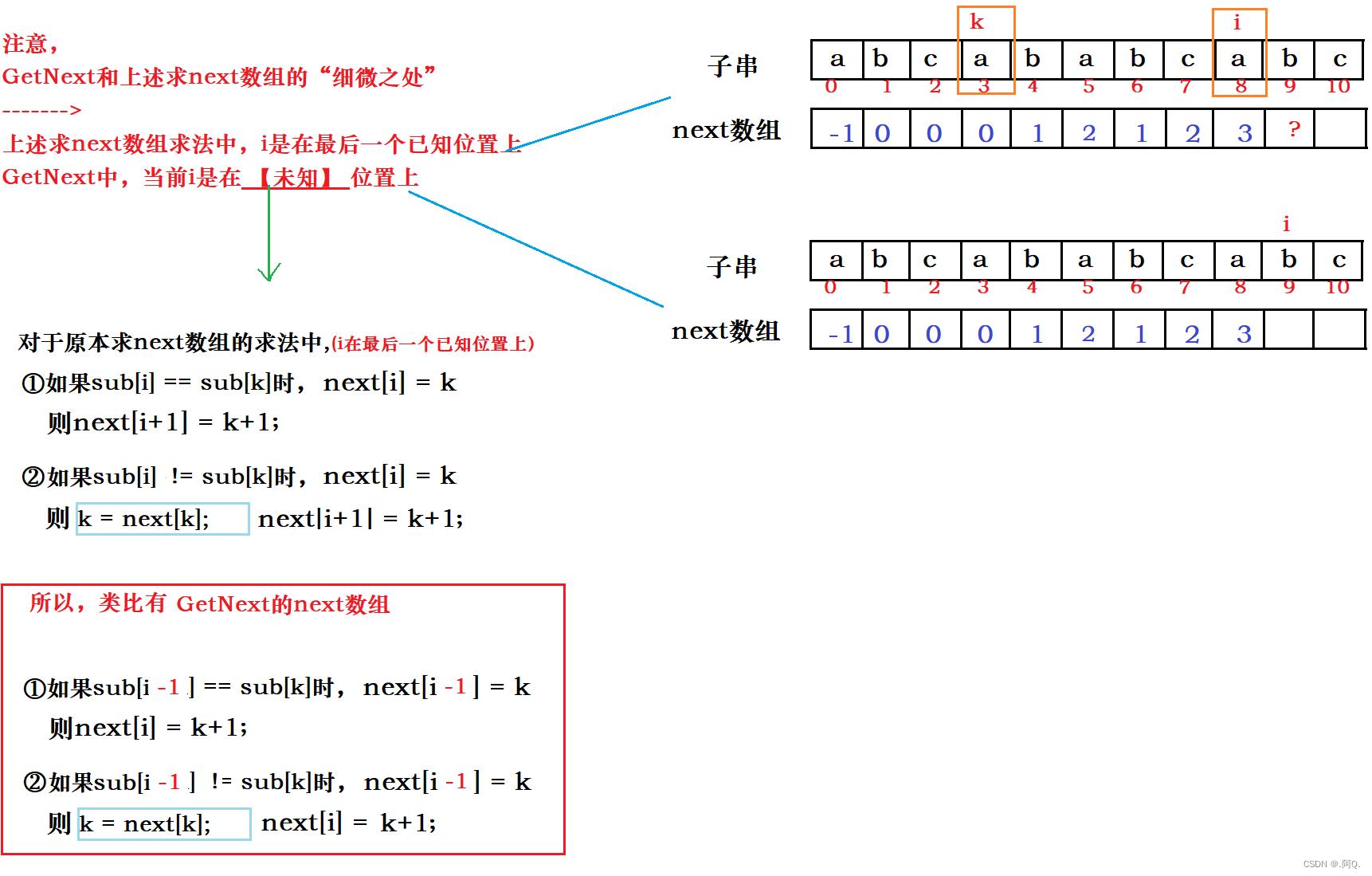
//next数组保存回退位置
void GetNext(char* sub, int* next, int lenSub)

	next[0] = -1;
	next[1] = 0;
	int i = 2;//当前i下标
	int k = 0;//前一项的k

	while (i <= lenSub)
	
		if (k == -1 || sub[i - 1] == sub[k])
		
			next[i] = k + 1;
			i++;
			k++;
		
		else
		
			k = next[k];
			next[i] = k + 1;
		
	

KMP算法

#include<stdio.h>
#include<string.h>
#include<assert.h>
#include<stdlib.h>
/*
KMP算法
str：主串
sub：子串
pos: 从子串的pos位置开始匹配
return：返回子串在主串当中的下标。如果不存在，则返回-1
*/
//next数组保存回退位置
void GetNext(char* sub, int* next, int lenSub)

	next[0] = -1;
	next[1] = 0;
	int i = 2;//当前i下标
	int k = 0;//前一项的k

	while (i <= lenSub)
	
		if (k == -1 || sub[i - 1] == sub[k])
		
			next[i] = k + 1;
			i++;
			k++;
		
		else
		
			k = next[k];
			next[i] = k + 1;
		
	

int KMP(char* str, char* sub, int pos)

	assert(str != NULL && sub != NULL);
	int lenStr = strlen(str);
	int lenSub = strlen(sub);
	if (lenStr == 0 || lenSub == 0) return -1;
	if (pos < 0 || pos >= lenStr) return -1;

	//next数组
	int* next = (int*)malloc(sizeof(int) * lenSub);
	GetNext(sub, next, lenSub);

	int i = pos;//遍历主串
	int j = 0;//遍历子串

	while (i < lenStr && j < lenSub)
	
		if (j == -1 || str[i] == sub[j])
		
			i++;
			j++;
		
		//一旦不匹配，就要使用到next数组来制定j的回退位置
		else
		
			j = next[j];
		
	

	//执行到这说明，主串和子串肯定存在有执行完的情况
	if (j >= lenSub)//说明子串执行完
	
		return i - j;
	
	return -1;


//int main()
//
//	printf("%d\\n", KMP("ababcfabcde", "abcd", 0));//6
//	printf("%d\\n", KMP("ababcfabcde", "abef", 0));//-1
//	printf("%d\\n", KMP("ababcfabcde", "ab", 0));//0
//
//	return 0;
//

3、KMP算法优化（优化next数组）

为什么要优化next数组？

比如如下字符串：

假设 i 在此处匹配失败了，那么 i 就会回退（i = next[i]），它会先回退到下标6，然后从下标6回退到下标5....最后回退到下标0；

可是我们可以发现，这个串回退没必要那么麻烦的！    前面都是一样的字符，我直接一次回退到下标0岂不是更好？

所以，对next数组进行优化是很有必要的。

next数组优化规则

next数组的优化，即：如何得到 nextval 数组，其优化规则如下：

1. 回退到的位置的字符和当前位置字符一样，就写回退到的那个位置的next值。
2. 如果回退到的位置的字符和当前字符不一样，就写当前字符原来的next值。

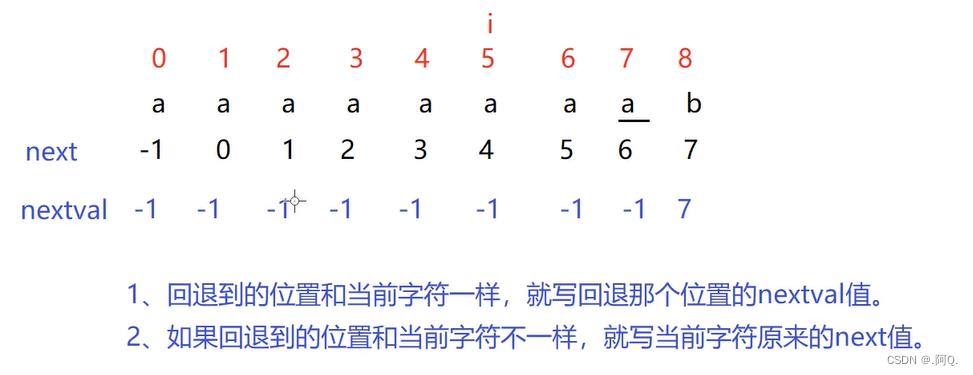
练习：

模式串 t = ‘   a   b   c   a   a   b   b   c   a   b   c   a   a   b   d   a   b   ’，该模式串的 next 数组的值为( D )   ，nextval 数组的值为(  F  )
A：0  1  1  1  2  2  1  1  1  2  3  4  5  6  7  1   2

B：0  1  1  1  2  1  2  1  1  2  3  4  5  6  1  1   2

C：0  1  1  1  0  0  1  3  1  0  1  1  0  0  7  0   1

D：0  1  1  1  2  2  3  1  1  2  3  4  5  6  7  1   2

E：0  1  1  0  0  1  1  1  0  1  1  0  0  1  7  0   1

F：0  1  1  0  2  1  3  1  0  1  1  0  2  1  7  0   1

注意：所求的题目中，问的next数组的值，需要在求出next基础上,全部加1