二叉堆树实现

Posted 2022-10-15 guardwhy

1.1 基本概念

二叉堆是一颗完全二叉树(区别于满二叉树)，堆中某个结点的值总是不大于其父节点的值，通常这种堆称为最大堆(相应的可以定义最小堆)，下层的某一元素不一定小于上层的某一元素。

1、大顶堆(最大堆)

最大堆的任何一个父节点的值，都大于或等于它左、右孩子节点的值。

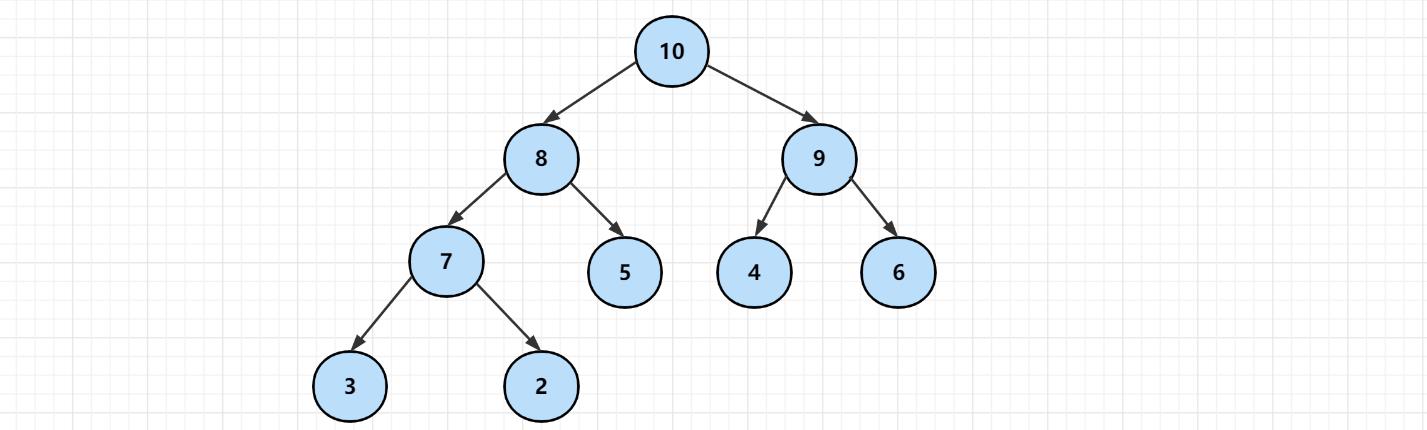
2、小顶堆(最小堆)

最小堆的任何一个父节点的值，都小于或等于它左、右孩子节点的值。

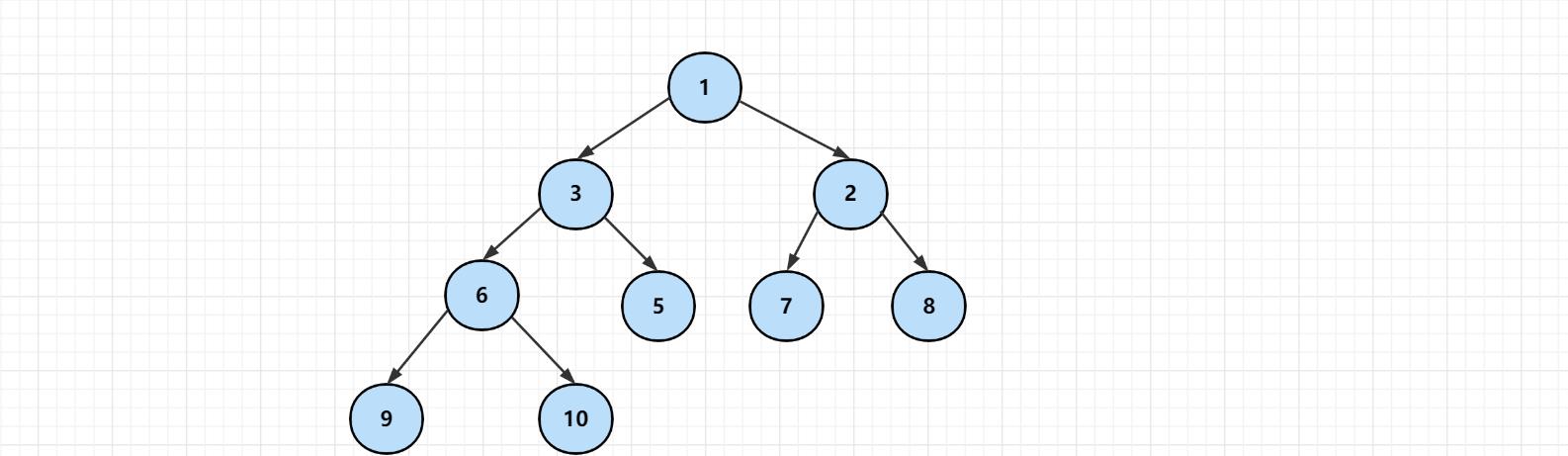
二叉堆的根节点叫作堆顶

最大堆和最小堆的特点决定了：最大堆的堆顶是整个堆中的最大元素，最小堆的堆顶是整个堆中的最小元素。

1.2存储原理

完全二叉树比较适合用数组来存储。用数组来存储完全二叉树是非常节省存储空间的。因为我们不需要存储左右子节点的指针，单纯地通过数组的下标，就可以找到一个节点的左右孩子节点和父节点。

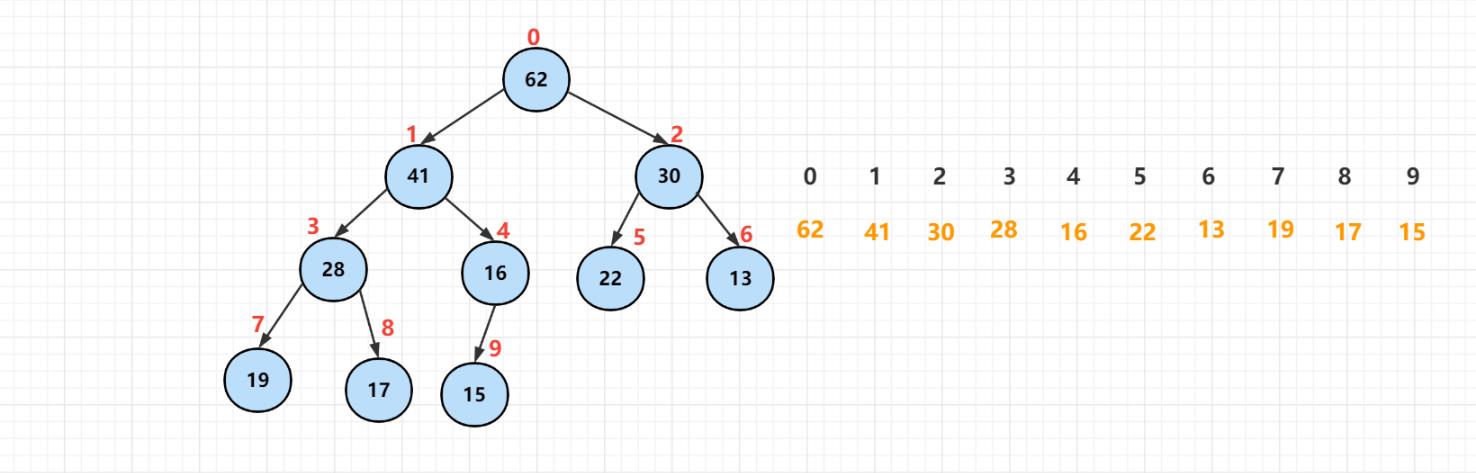
从图中我们可以看到，数组中下标为 i 的节点的左子节点，就是下标为left child(i) = i∗2 +1的节点，右子节点就是下标为right child(i) = i∗2 +2的节点，父节点就是下标为parent(i) = (i-1) /2取整的节点。

1.3 思路分析

1、添加元素

堆中的元素是使用数组的样式排列的，添加元素相当于是层序遍历的最右边，也就是最下面一层的最右添加元素，从数组的表示角度就是在索引为【10】的位置添加了元素【52】这个值。

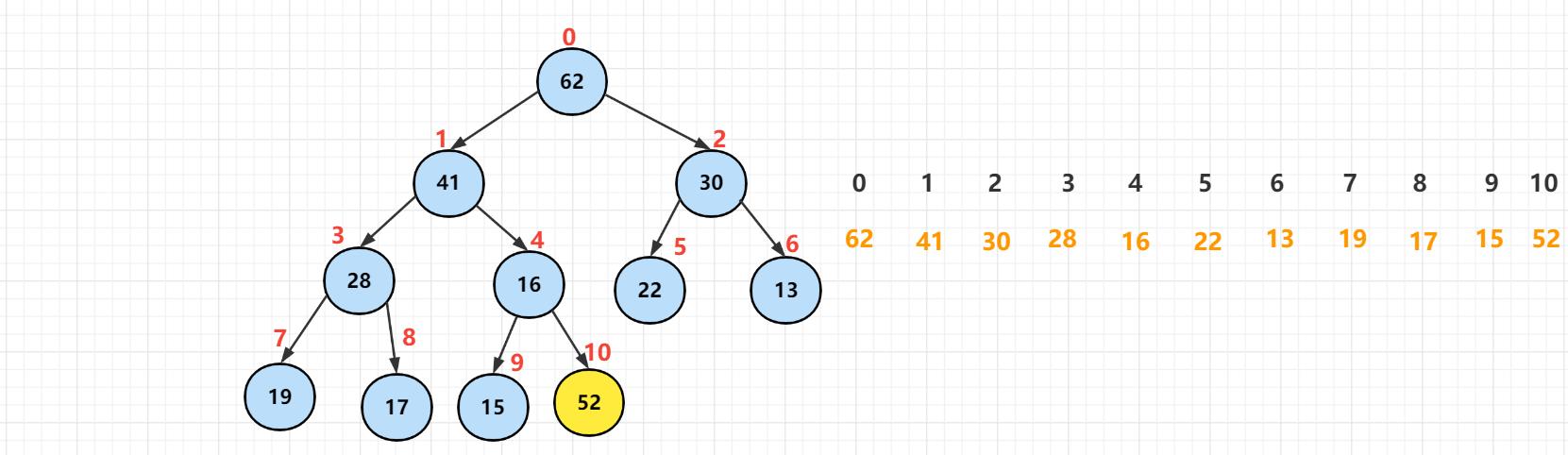
这显然不满足堆的性质，所有要拿添加的元素跟父节点进行比较，发现元素【52】比【16】大，所以需要交换两个元素的位置。

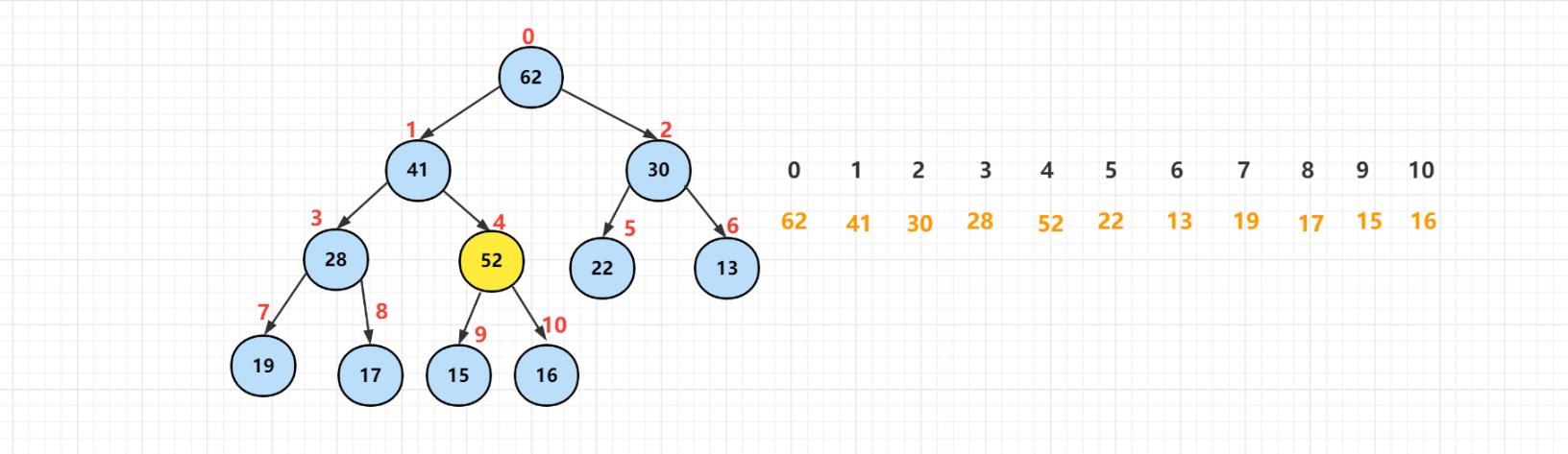
以【52】为根的二叉树满足了堆的性质，但是这样明显不够的，【52】这个节点比它的父节点【41】还要大，所以两者之间还要进行元素交换。

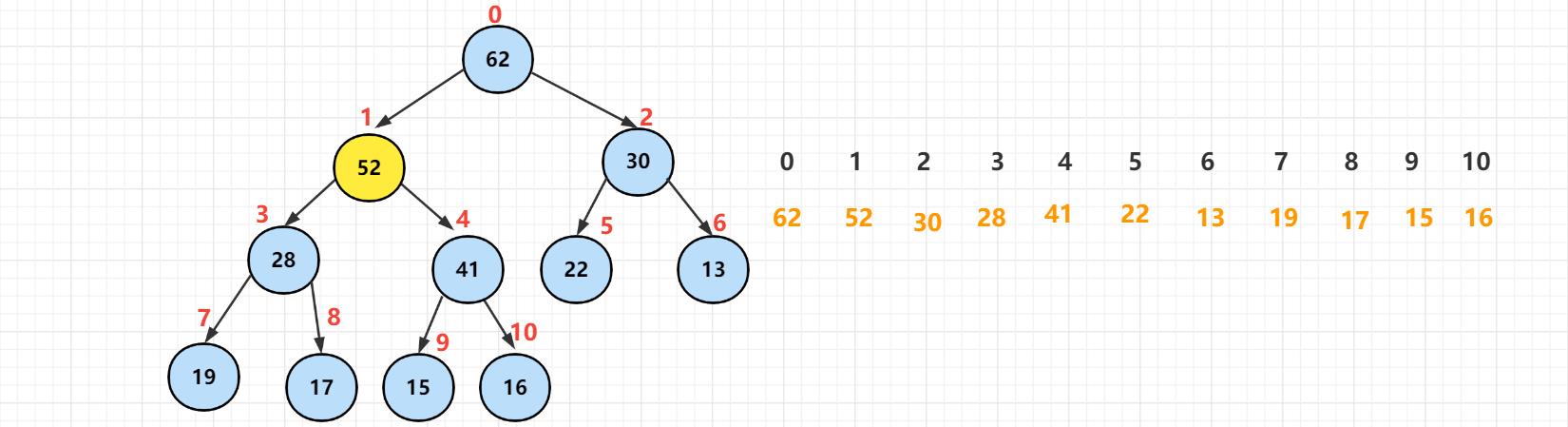
此时【52】是小于【62】这个元素节点的，满足堆的性质。所以在这个位置上没有破坏堆的性质。

2、删除元素

从堆中取出元素，只拿出最大的元素，堆顶元素，取出堆顶元素。

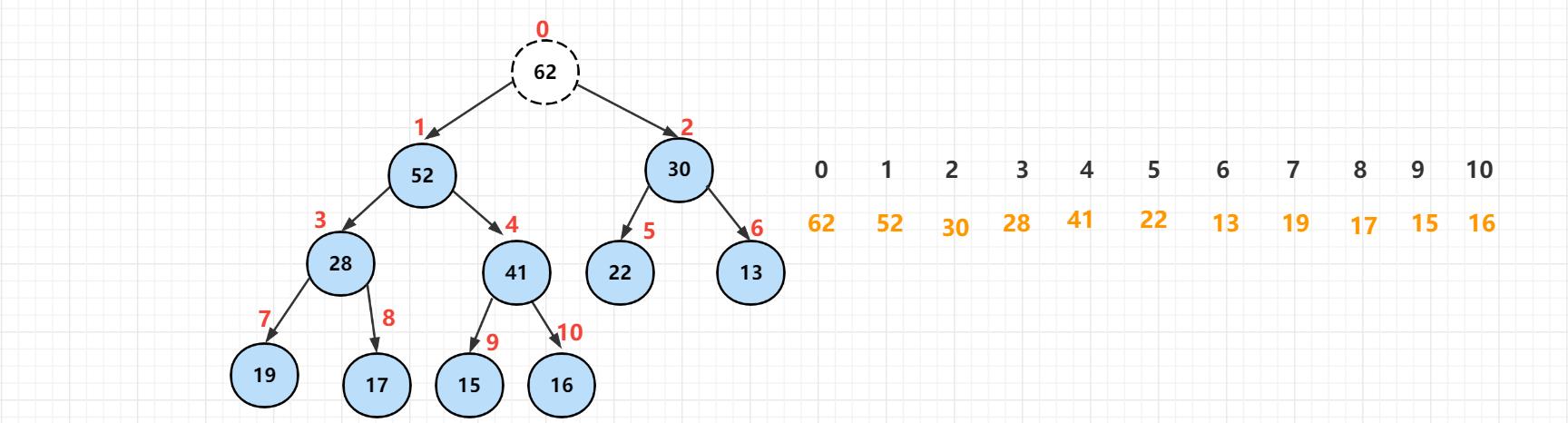
将堆中的最后元素【16】顶到堆顶去，这样操作完以后，索引为0的元素为【16】，最后一个元素也是16，然后将最后一个元素删除。从元素的个数上成功的减少了一个元素，并且就是堆顶的那个元素。

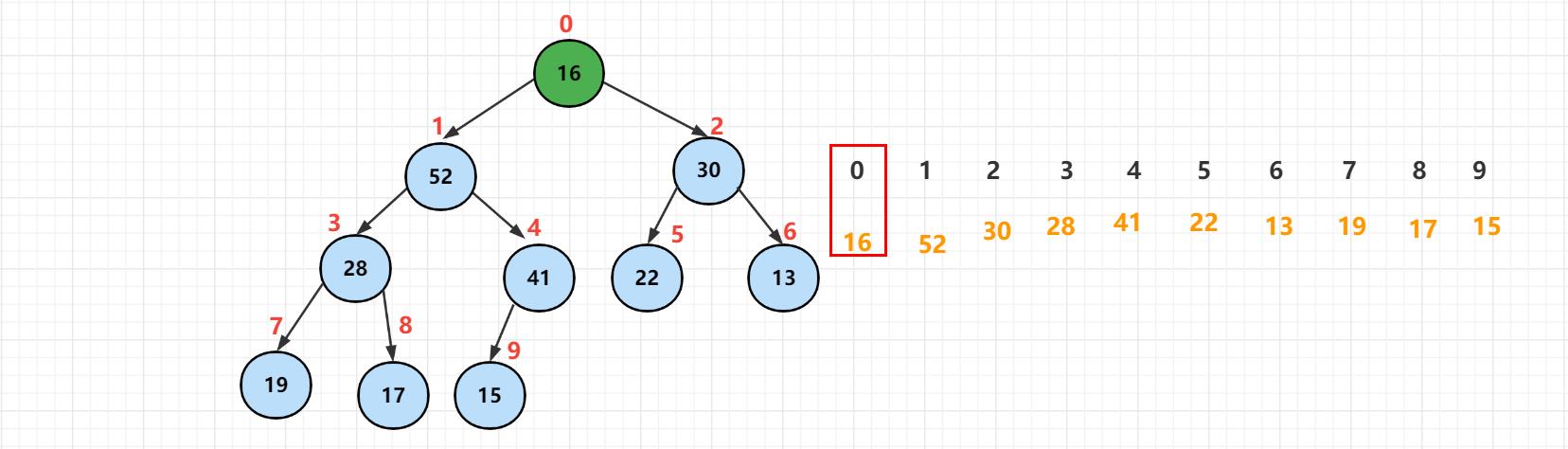
不过现在堆顶的元素打破了堆的性质，此时应该执行下沉操作，让下沉元素跟它的左右孩子进行比较。选择孩子中最大的那个元素，如果小于最大的那个元素，那么就进行交换。

然后继续比较，继续交换。

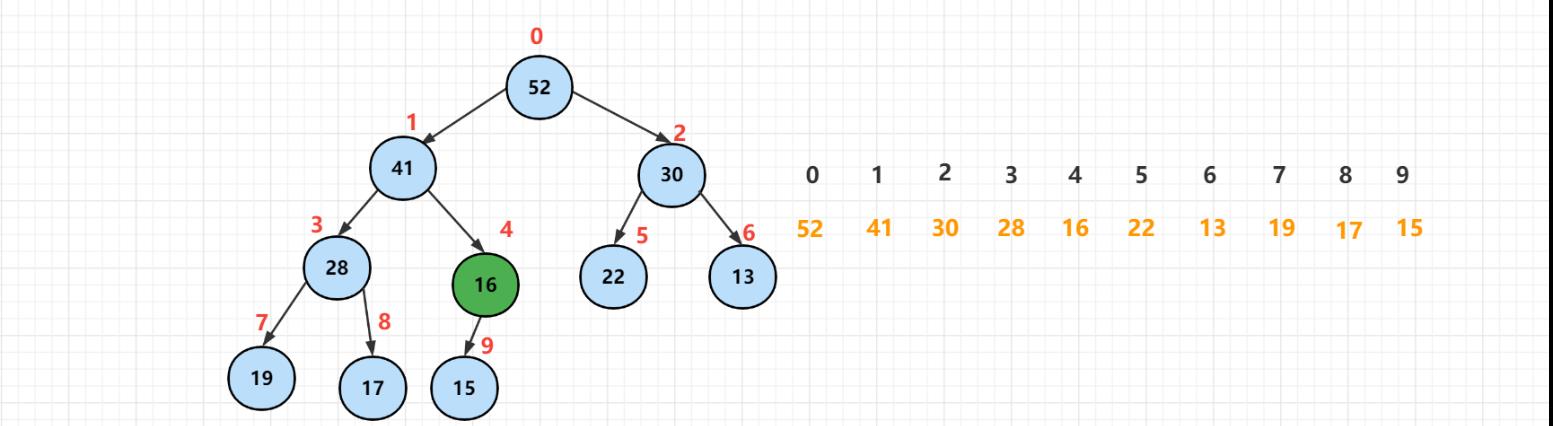
此时下沉节点比15要大，满足堆的基本性质，此时下沉操作已经结束了。

1.4 代码实现

1、顺序表：ArrayList

package cn.heap.demo01;

import java.util.Iterator;

public class ArrayList<E> implements Iterable<E>
    // 顺序表的元素
    private E[] data;
    // 顺序表元素的数量
    private int size;

    // 定义常量
    private static final int ELEMENT_NOT_FOUND = -1;
    private static final int DEFAULT_CAPACITY = 6;

    // 元素的数量
    public int size() 
        return size;
    

    //清除所有元素
    public void clear() 
        for (int i = 0; i < size; i++) 
            data[i] = null;
        
        size = 0;
    


    // 构造函数，传入数组的容量capacity构造SqList
    public ArrayList(int capacity)
        data = (E[]) new Object[capacity];
        capacity = (capacity < DEFAULT_CAPACITY) ? DEFAULT_CAPACITY : capacity;
    

    // 无参数的构造函数，默认数组的容量capacity=10
    public ArrayList()
        this(DEFAULT_CAPACITY);
    

    // 获取数组的容量
    public int getCapacity()
        return data.length;
    

    // 获取数组中的元素个数
    public int getSize()
        return size;
    

    // 返回数组是否为空
    public boolean isEmpty()
        return size == 0;
    

    // 向所有元素后添加一个新元素
    public void addLast(E e)
        add(size, e);
    

    // 在所有元素前添加一个新元素
    public void addFirst(E e)
        add(0, e);
    

    // 在index索引的位置插入一个新元素e
    public void add(int index, E e)
        // 扩容操作
        if(size == data.length)
           resize(2 * data.length);
        

        for(int i = size - 1; i >= index ; i --)
            data[i + 1] = data[i];
        

        data[index] = e;
        size ++;
    

    // 获取index索引位置的元素
    public E get(int index)
        rangeCheck(index);
        return data[index];
    

    // 查看元素的索引
    public int indexOf(E e)
        if (e == null) 
            for (int i = 0; i < size; i++) 
                if (data[i] == null) return i;
            
         else 
            for (int i = 0; i < size; i++) 
                if (e.equals(data[i])) return i;
            
        
        return ELEMENT_NOT_FOUND;
    

    // 修改index索引位置的元素为e
    public void set(int index, E e)
        rangeCheck(index);
        data[index] = e;
    

    // 查找数组中是否有元素e
    public boolean contains(E e)
       return indexOf(e) != ELEMENT_NOT_FOUND;
    

    // 查找数组中元素e所在的索引，如果不存在元素e，则返回-1
    public int find(E e)
        for(int i = 0 ; i < size ; i ++)
            if(data[i].equals(e))
                return i;
        
        return -1;
    

    // 从数组中删除index位置的元素, 返回删除的元素
    public E remove(int index)
        rangeCheck(index);
        E ret = data[index];
        for(int i = index + 1 ; i < size ; i ++)
            data[i - 1] = data[i];
        
        // 置空
        data[--size] = null;

        // 缩容操作
        if(size == data.length / 4)
            resize(data.length / 2);
        
        return ret;
    

    // 从数组中删除第一个元素, 返回删除的元素
    public E removeFirst()
        return remove(0);
    

    // 从数组中删除最后一个元素, 返回删除的元素
    public E removeLast()
        return remove(size - 1);
    

    // 从数组中删除元素e
    public void removeElement(E e)
        int index = find(e);
        if(index != -1) 
            remove(index);
        
    

    // 数组索引越界处理
    private void outOfBounds(int index)
        throw new IndexOutOfBoundsException("index:" + index + ", Size:" + size);
    

    // 索引值检查范围方法
    private void rangeCheck(int index)
        if(index < 0 || index >=size)
            // 调用越界处理方法
            outOfBounds(index);
        
    

    // 添加方法索引检查范围
    private void rangeCheckAdd(int index)
        if(index < 0 || index >size)
            // 调用越界处理方法
            outOfBounds(index);
        
    

    // 扩容capacity方法
    private void resize(int newCapacity)
        E[] newData = (E[])new Object[newCapacity];
        for(int i = 0 ; i < size ; i ++)
            newData[i] = data[i];
        
        data = newData;
    

    @Override
    public String toString()
        StringBuilder res = new StringBuilder();
        res.append(String.format("顺序表(ArrayList)长度:%d, 容器:%d\\n", size, data.length));
        res.append('[');
        for(int i = 0 ; i < size ; i ++)
            res.append(data[i]);
            if(i != size - 1)
                res.append(", ");
        
        res.append(']');
        return res.toString();
    

    // 交换方法
    public void swap(int i, int j)
        E temp = data[i];
        data[i] = data[j];
        data[j] = temp;
    

    // 遍历方法
    @Override
    public Iterator<E> iterator() 
        return new SIterator();
    

    private class SIterator implements Iterator
        // 定义一个指针变量
        private int cur;
        public SIterator()
            this.cur=0;
        
        @Override
        public boolean hasNext() 
            return cur< size;
        
        @Override
        public E next() 
            return data[cur++];
        
    

2、最大堆：MaxHeap

package cn.heap.demo01;

import java.util.Iterator;

/***
 * 最大堆实现
 * @param <E>
 */
public class MaxHeap<E extends Comparable<E>> implements Iterable<E>
    // 用ArrayList当做最大堆的存储容器
    private ArrayList<E> data;
    // 堆空间
    public MaxHeap()
        data = new ArrayList<>();
    

    // 获取父节点的索引
    private int parent(int k)
        if(k <= 0)
            throw new IllegalArgumentException("没有父节点!");
        
        return (k -1 ) / 2;
    

    // 获取左孩子结点的索引
    private int leftChild(int k)
        return 2 * k + 1;
    

    // 获取右孩子结点的索引
    private int rightChild(int k)
        return 2 * k + 2;
    

    // 返回最大堆有效元素的个数
    public int size()
        return data.size();
    

    // 判断二叉堆是否为空
    public boolean isEmpty()
        return data.isEmpty();
    

    // 清空二叉堆
    public void clear()
        data.clear();
    

    // 向最大堆中添加一个元素e
    public void add(E e)
        data.addLast(e);
        // 上浮元素对应的索引
        siftUp(data.size() -1);
    

    // 将角标K所对应的元素进行上浮
    private void siftUp(int k)
        // 父亲节点比自己还要小的话，交换元素
        while (k > 0 && data.get(k).compareTo(data.get(parent(k))) < 0)
            data.swap(k, parent(k));
            k = parent(k);
        
    

    // 找到最大堆
    public E findMax()
        if (data.isEmpty())
            throw new IllegalArgumentException("最大堆为空!!!!");
        
        return data.get(0);
    

    // 最小堆
    public E findMin()
        if(data.isEmpty())
            throw new IllegalArgumentException("最大堆为空!!!");
        
        E min = data.get(0);
        for (int i=1; i< data.size(); i++)
            if(data.get(i).compareTo(min) < 0)
                min = data.get(i);
            
        
        // 返回最小堆
        return min;
    

    // 删除最大值
    public E extractMax()
        // 拿到最大值
        E max = findMax();
        // 将索引为0和最后一个元素交换位置
        data.swap(0, data.size() - 1);
        // 将最后一个元素删除
        data.remove(data.size() - 1);

        // 调用函数
        siftDown(0);
        return max;
    

    // 下浮
    private void siftDown(int k) 
        while (leftChild(k) < data.size())
            // 拿到左右孩子的最大值
            int j = leftChild(k);
            if(j + 1 < data.size() && data.get(j+1).compareTo(data.get(j)) > 0)
                // data[j] 是leftChild和rightChild中的最大值
                j = rightChild(k);
            
            if(data.get(k).compareTo(data.get(j)) < 0)
                data.swap(k,j);
                k = j;
            else 
                break;
            
        
    

    // 取出最大元素后，放入一个新元素
    public E replace(E e)
        E ret = findMax();
        data.set(0, e);
        siftDown(0);
        return ret;
    

    @Override
    public Iterator<E> iterator() 
        return data.iterator();
    

    @Override
    public String toString()
        return data.toString();
    

3、测试类：TestMaxHeap

package cn.heap.demo01;

import java.util.Random;

public class TestMaxHeap 
    public static void main(String[] args以上是关于二叉堆树实现的主要内容，如果未能解决你的问题，请参考以下文章
 
 二叉堆树实现
 二叉堆树实现
 堆树中的第 K 个元素
 基本数据结构——二叉堆
 堆排序
 二叉堆的所有用途